LC1552.两球之间的磁力

原题链接：https://leetcode.cn/problems/magnetic-force-between-two-balls/

在代号为 C-137 的地球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 个空的篮子，第 个篮子的位置在 ，Morty 想把 个球放到这些篮子里，使得任意两球间 最小磁力 最大。 已知两个球如果分别位于 和 ，那么它们之间的磁力为 。 给你一个整数数组 和一个整数 ，请你返回最大化的最小磁力。

• 示例 1：

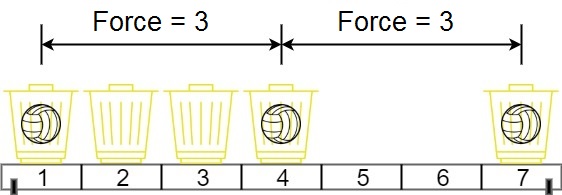
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。

示例 2：

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

• 提示：
• 
• 
• 
• 所有 中的整数 互不相同 。

• 

  思路：用二分查找代替暴力遍历

• 希望球的最短间距的最大值尽量大一点

• 假如只有两个球，此时的“最短间距”一定是最大的。
• 如果加入更多的球，那么此时的“最短间距最大值”就会慢慢降低。
• 那么，对于“最短间距的最大值”这个区间来讲，越是小就越能符合条件，所以，相当于取左边数组的右端点。
• 假如现在已经知道了球的间距dis，如果算出怎么才能放入最多数量的球呢? 结合了贪心算法的想法：

• pre_pos记录上一个符合条件的球的位置，初始化为position[0]，计数器cnt统计放球的数量，初始化为1，遍历筐子的分布位置数组position，如果满足position[i] - pre_pos >= dis，那么执行两步操作：1.更新pre_pos为当前的position[i]，2.计数器cnt += 1

  代码：

  class Solution {
  public:
    bool check(int dis, vector<int>& position, int m) {
        int all_num = 1;
        int pre_pos = position[0];
        for (int pos : position) {
            if (pos - pre_pos >= dis) {
                all_num += 1;
                pre_pos = pos;
            }
        }
        // cout << all_num << endl;
        return all_num >= m;
    }
    int maxDistance(vector<int>& position, int m) {
        // 按照某种最优的方法，最小距离越大，球的数量就越少
        // 逐步升高最小距离，直到球的数量恰好是m个
        // 相当于取左区间的右端点
        sort(position.begin(), position.end());
        int left = 1, right = 1e9 + 5;
        while (left < right) {
            int mid = (left + right + 1) / 2;
            if (check(mid, position, m)) {
                left = mid;
            } else {
                right = mid - 1;
            }
        } 
        // check(3, position, 3);
        return left;
    }
  };