LC139. 单词拆分

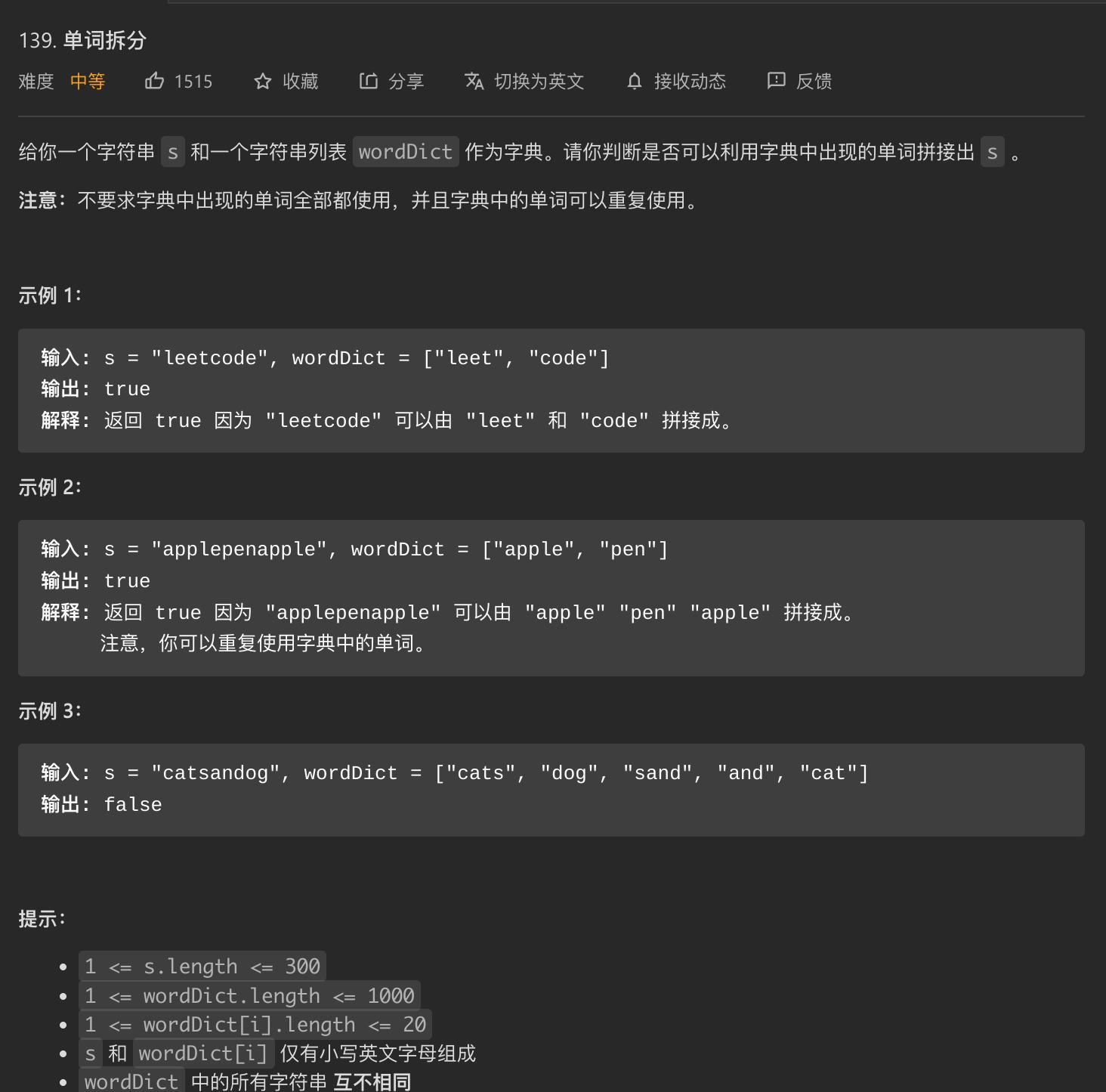
思路：字典树 + 回溯 + 记忆化搜索

• 此题的正解应该是动态规划，但是字典树也可以做
• 对于wordDict中的每一个word，都需要直通根节点地放置在字典树当中。每个单词的地位是平等的。
• 对于目标字符串s而言，如果读到了isEnd标志，意味着当前单词读完了，就重新从根节点开始找起，找下一个单词，不断重复这个操作，似乎可以找完整棵树。
• 但是如果出现前缀相同的情况，比如app apple，先读到app的终结标志，直接就开始找下一个字符了，显然不对，所以需要回溯。
• 但是回溯时间复杂度指数级增长，所以需要用failCase[i]来表示以第i位的字符开头，必然无法找到需要的单词，防止重复回溯。

代码：

class TrieNode:
    def __init__(self):
        self.isEnd = False
        self.children = [None for _ in range(26)]
    def insert(self, wordDict: List[str]) -> None:
        # 把所有的字符串放到同一个字典当中
        # 根节点 - leet && 根节点 -- code
        trieRoot = self
        for word in wordDict:
            curNode = trieRoot
            for ch in word:
                chNum = ord(ch) - ord('a')
                if curNode.children[chNum] == None:
                    curNode.children[chNum] = TrieNode()
                curNode = curNode.children[chNum]
            curNode.isEnd = True
class Solution:
    def __init__(self):
        # 为记忆化搜索做准备
        self.failedCase = [False for _ in range(310)]
    def search(self, rootNode: TrieNode(), s: str, beginPos: int) -> bool:
        # 记忆化搜索，以beginPos开头的必然不在字典中，所以下次遍历到这个位置的时候直接返回
        if self.failedCase[beginPos]:
            return False
        if beginPos == len(s):
            return True
        curNode = rootNode
        while beginPos < len(s):
            chNum = ord(s[beginPos]) - ord('a')
            if curNode.children[chNum] == None:
                return False
            curNode = curNode.children[chNum]
            # 回溯
            if curNode.isEnd:
                if (self.search(rootNode, s, beginPos + 1)):
                    return True
                else:
                    self.failedCase[beginPos + 1] = True
            beginPos += 1
        return False
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        rootNode = TrieNode()
        rootNode.insert(wordDict)
        return self.search(rootNode, s, 0)