思路：回溯

• 我的解法和官方题解不一样，官方题解更加直观，但是我的解法建立的树更加小
• 官方题解的做法是“二叉树式的组合回溯”，左孩子选，右孩子不选
• 我的解法是“数组的最后一个元素作为叶子节点的组合回溯”方法，使用了for循环
• 脑力里面要有图，两张图的区别要搞清楚

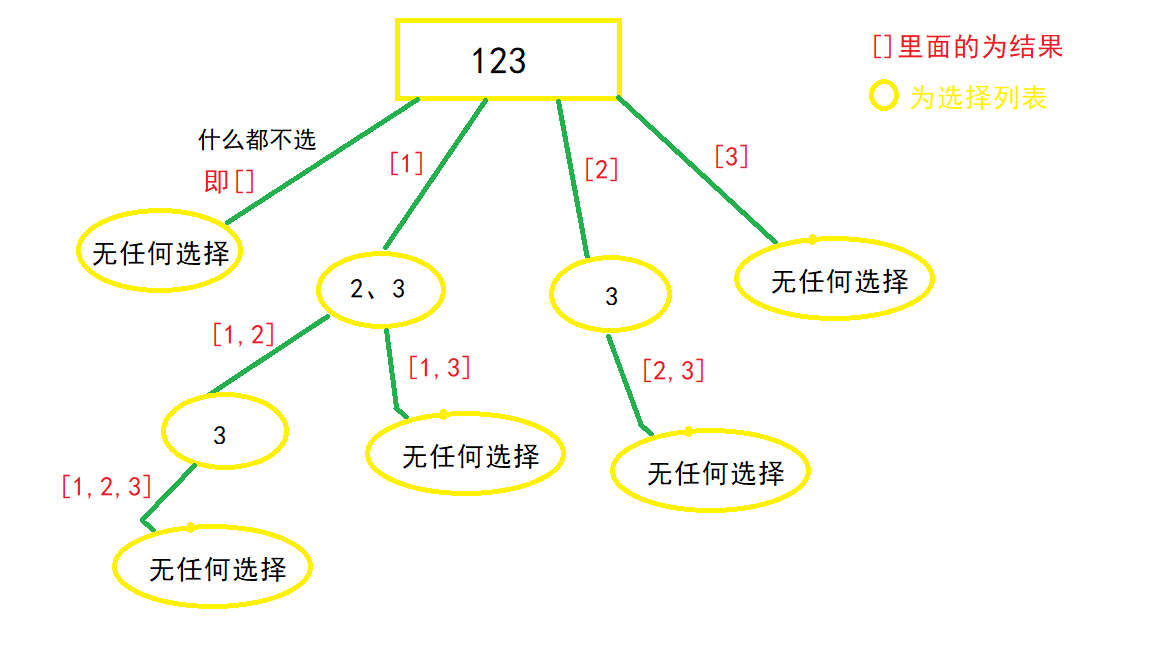
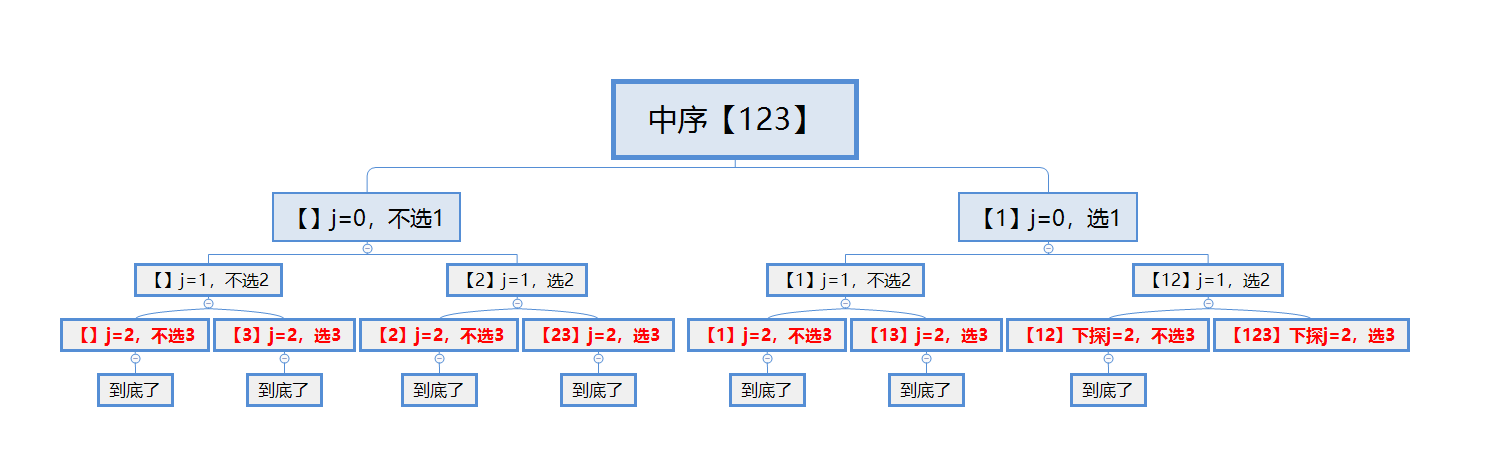
代码：

class Solution {
public:
    void backTrack(vector<int>& t, vector<vector<int>>& ans, int cur, vector<int>& nums) {
        ans.push_back(t);
        if (cur == nums.size()) {
            return;
        }
        for (int i = cur; i < nums.size(); ++i) {
            t.push_back(nums[i]);
            backTrack(t, ans, i + 1, nums);
            t.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<int> t;
        vector<vector<int>> ans;
        backTrack(t, ans, 0, nums);
        return ans;
    }
};

思路2：位运算暴搜

• 枚举所有情况，子集问题近似于二进制枚举的本质，逐个枚举，遍历所有子集

• 枚举所有情况

  for (int S = 0; S < (1 << n); ++S) {

• 从低位开始检查是否选用当前元素

for (int i = 0; i < n; i++) {
     if (S & (1 << i)) {
        t.push_back(nums[i]);
    }
}

代码2

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> ans;
        int n = nums.size();
        for (int S = 0; S < (1 << n); ++S) {
            vector<int> t;
            for (int i = 0; i < n; i++) {
                if (S & (1 << i)) {
                    t.push_back(nums[i]);
                }
            }
            ans.push_back(t);
        }
        return ans;
    }
};