快速排序(QuickSort)

概要

快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。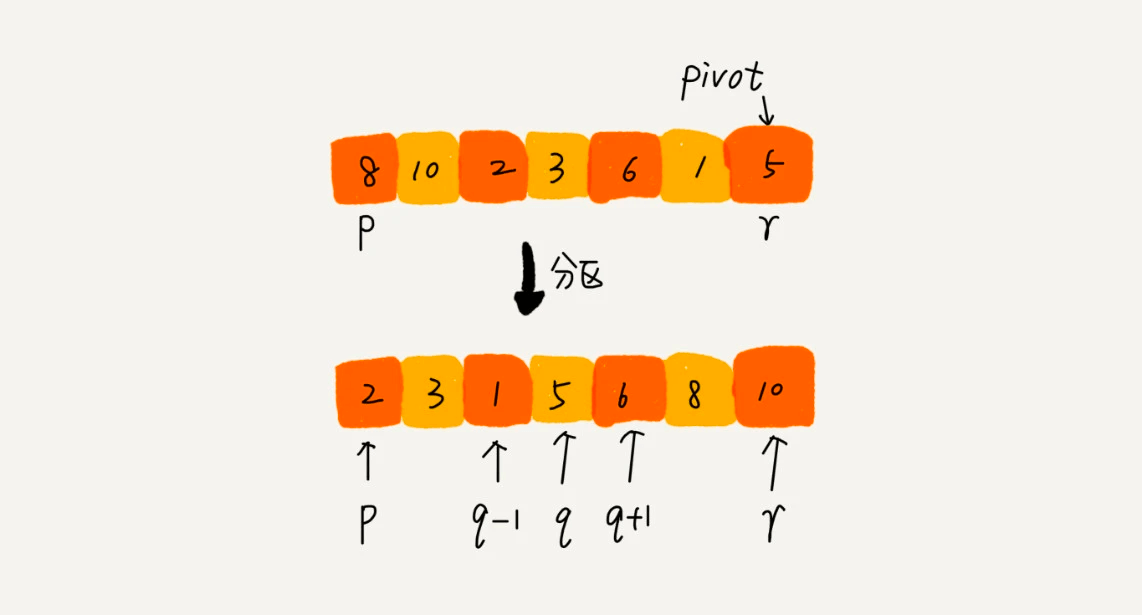

根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。
如果我们用递推公式来将上面的过程写出来的话，就是这样：

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)
终止条件：
p >= r

原理

将递推公式转换为代码如下：

// 快速排序，a是数组，n表示数组的大小
static void quickSort(int[] a, int n) {
    quickSortInternally(a, 0, n-1);
}
  // 快速排序递归函数，p,r为下标
static void quickSortInternally(int[] a, int p, int r) {
    if (p >= r) return; // 逐层分解到最后一个元素终止递归
    int partition = partition(a, p, r); // 获取分区点
    quickSortInternally(a, p, partition-1);
    quickSortInternally(a, partition + 1, r);
}

归并排序中有一个 merge() 合并函数，快速排序有一个 partition() 分区函数。partition() 分区函数就是随机选择一个元素作为 pivot分区值（一般情况下，可以选择 p 到 r 区间的最后一个元素或数组的第一个元素），然后对 A[p…r]分区，函数返回 pivot 的下标。
分区函数算法

static int partition(int[] data, int p, int r) {
    int pivot = data[p]; // 默认取数组第一个值为分区值
    int left = p;
    int right = r;
    while (left < right) {
        // 1. 从左开始查找大于分区值的元素
        while (data[left] <= pivot && left < right) {
            left++;
        }
        // 2.从右边开始查找小于分区值的元素
        while (data[right] > pivot) {
            right--;
        }
        // 如果left与right未相遇,则交换
        if (left < right) {
            int temp = data[left];
            data[left] = data[right];
            data[right] = temp;
        }
    }
    // 循环结束，表示找到了一个分区位置，该位置坐标的数据比分区值小，右边的数据比分区大
    // 由于默认的分区值为数组第一个元素，因此需要交换数据，并返回真正的分区下标位置
    int temp = data[p];
    data[p] = data[right];
    data[right] = temp;
    System.out.println(String.format("查找分区点,[p=%d,r=%d],pivot=%d", p, r, right));
    return right;
 }

测试

public static void main(String[] args) {
    int[] data = new int[]{90, 65, 7, 305, 120, 110, 8};
    System.out.println("Before Sort\n" + Arrays.toString(data));
    quickSort(data, data.length);
    System.out.println("After QuickSort\n" + Arrays.toString(data));
}

说明

1）快速排序是一种原地排序算法，空间复杂度为O(1), 因为其实现上是基于原数组空间，不需要申请额外的内存即可完成排序
2）由于排序过程中，涉及到交换，因此快速排序不是稳定的排序算法(元素原有的相对位置可能会发生改变）
3）快速排序在大部分情况下的时间复杂度都可以做到 O(nlogn)，在极端情况下，会退化到 O(n2)。

实践

O(n) 时间复杂度内求无序数组中的第 K 大元素？比如，4， 2， 5， 12， 3 这样一组数据，第 3 大元素就是 4。
快排核心思想就是分治和分区，我们可以利用分区的思想来解决。
我们选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot，对数组 A[0…n-1]原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。
如果 p+1=K，那 A[p]就是要求解的元素；如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间，递归地在 A[p+1…n-1]这个区间内查找。同理，如果 K

/**
     * 基于快排的分区分治思想查询第K大的元素
     * @param data
     * @param k
     * @return
     */
public static int findKLargestByQuickPartition(int[] data, int k) {
    if (data == null || data.length < k) {
        return -1;
    }
    // [0....p-1] [p] [p+1....n-1]
    int partition = partition(data, 0, data.length - 1); // 获取分区点
    while (partition + 1 != k) { // 为什么是+1,因为数组下标是从0开始,第K个最大值其实就是分区值+1后的下标
        if (k > partition + 1) {
            partition = partition(data, partition + 1, data.length - 1); // 获取分区点
        } else {
            partition = partition(data, 0, partition - 1); // 获取分区点
        }
    }
    return data[partition];
}
/**
     * 分区函数：该函数可以减少交换次数
     * 查找一个分区值，大于该值的在左边，小于该值的在右边
     * @param data
     * @param p
     * @param r
     * @return
     */
private static int partition(int[] data, int p, int r) {
    int pivot = data[p]; // 默认取数组第一个值为分区值
    int left = p;
    int right = r;
    while (left < right) {
        // 1. 从左开始查找小于分区值的元素
        while (data[left] >= pivot && left < right) {
            left++;
        }
        // 2.从右边开始查找大于分区值的元素
        while (data[right] < pivot) {
            right--;
        }
        // 如果left与right未相遇,则交换
        if (left < right) {
            int temp = data[left];
            data[left] = data[right];
            data[right] = temp;
        }
    }
    // 由于默认的分区值为数组第一个元素，因此需要交换数据，并返回真正的分区下标位置
    int temp = data[p];
    data[p] = data[right];
    data[right] = temp;
    System.out.println(String.format("查找分区点,[p=%d,r=%d],pivot=%d", p, r, right) + ",Data=" + Arrays.toString(data));
    return right;
}

为什么上述解决思路的时间复杂度是 O(n)？
第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。依次类推，分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。如果我们把每次分区遍历的元素个数加起来，就是：n+n/2+n/4+n/8+…+1。这是一个等比数列求和，最后的和等于 2n-1。所以，上述解决思路的时间复杂度就为 O(n)。