插入排序算法原理

设有一组关键字｛K1， K2，…， Kn｝；排序开始就认为 K1 是一个有序序列；让 K2 插入上述表长为 1 的有序序列，使之成为一个表长为 2 的有序序列；然后让 K3 插入上述表长为 2 的有序序列，使之成为一个表长为 3 的有序序列；依次类推，最后让 Kn 插入上述表长为 n-1 的有序序列，得一个表长为 n 的有序序列。
具体算法描述如下：

  1. 从第一个元素开始，该元素可以认为已经被排序
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
  4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤 2~5

如果比较操作的代价比交换操作大的话，可以采用二分查找法
来减少比较操作的数目。该算法可以认为是插入排序的一个变种，称为二分查找排序。
二分查找法，是一种在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

实例分析与代码实现

现有一组数组 arr = [5, 6, 3, 1, 8, 7, 2, 4]，共有八个记录，采用上述算法步骤，执行顺序为：

  1. 第一个数：5 已默认排序
  2. 从第二个数：6 开始，依次与前一个比较，如果比前一个数小，则交换，否则不交换
  3. 继续向前找
    1. 5   6   3   1   8   7   2   4
    2. ↑   │
    3. └───┘(no swap)
    4. 5   6   3   1   8   7   2   4
    5.  ↑   │(swap)
    6. 5   3   6   1   8   7   2   4
    7. 5   3   6   1   8   7   2   4
    8. ↑   │(swap)
    9. 3   5   6   1   8   7   2   4   
    10. ....

具体做法是，将新元素取出，从左到右依次与已排序的元素比较，如果已排序的元素大于新元素，那么将该元素移动到下一个位置，接着再与前面的已排序的元素比较，直到找到已排序的元素小于等于新元素的位置，这时再将新元素插入进去，就像下面这样：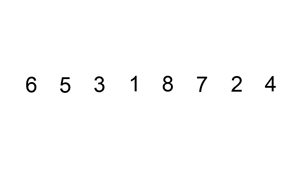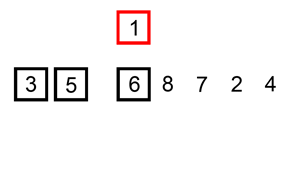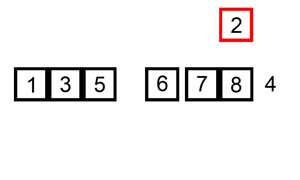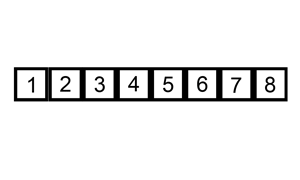
Insertion-sort-example-300px.gif
上述做法可以减少交换的次数，是一种插入目标到已排好序的序列中,代码实现为：

  1. static void insertSortInternally(int[] data) {
  2.     // 从下标为1的元素开始选择合适的位置插入，因为下标为0的只有一个元素，默认是有序的
  3.     for (int i = 1; i < data.length; i++) {
  4.         int v = data[i]; // 记录要插入的数据
  5.         int position = i;
  6.         // 如果下一个数左边已排序好的序列小,则依次向右边移动
  7.         while (position > 0 && data[position - 1] > v) {
  8.             data[position] = data[position-1];
  9.             position--;
  10.         }
  11.         data[position] = v;
  12.     }
  13. }

算法分析

1）插入排序是一种稳定排序算法（前后元素相对位置不变）

在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

2）插入排序平均时间复杂度为 O(n2)

如果要排序的数据已经是有序的，我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置，每次只需要比较一个数据就能确定插入的位置。所以这种情况下，最好是时间复杂度为 O(n)。注意，这里是从尾到头遍历已经有序的数据。如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，所以最坏情况时间复杂度为 O(n2)。还记得我们在数组中插入一个数据的平均时间复杂度是多少吗？没错，是 O(n)。所以，对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行 n 次插入操作，所以平均时间复杂度为 O(n2)。

3) 插入排序是原地排序算法，空间复杂度为O(1)

从实现过程可以很明显地看出，插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O(1)，也就是说，这是一个原地排序算法。

为什么插入排序比冒泡或选择排序有用？

插入排序有更少的元素交换次数，即有更少的代码执行时间，性能较好。