概要

归并排序，即合并排序，如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。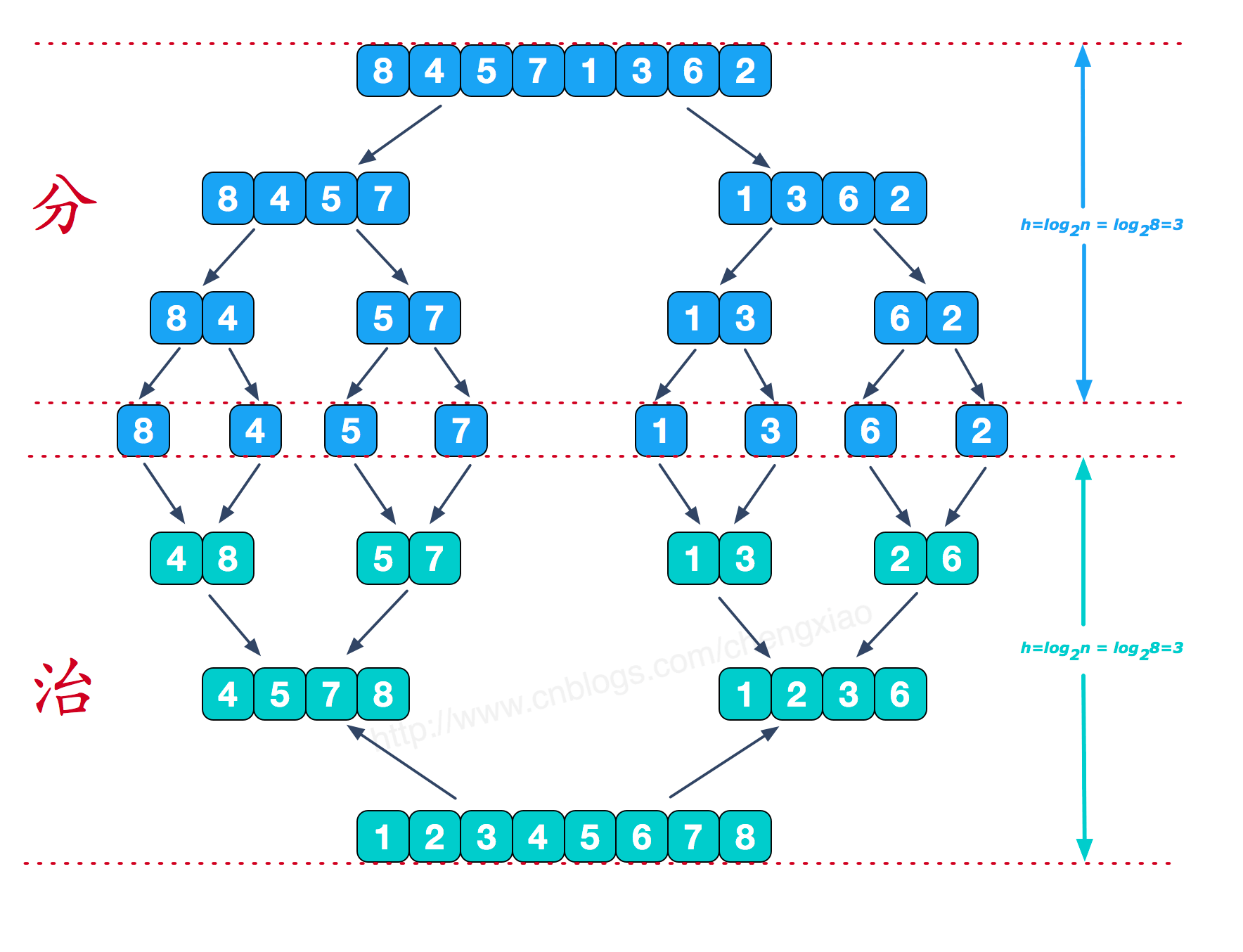
image.png

排序原理

归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。分治算法一般都是用递归来实现的。

注:分治是一种解决问题的处理思想，递归是一种编程技巧.

  1. 递推公式：
  2. merge_sort(left…right) = merge(merge_sort(left…mid), merge_sort(mid+1…right))
  4. 终止条件：
  5. left >= right 不用再继续分解

merge_sort(left…right) 表示，给下标从 left 到 right之间的数组排序。我们将这个排序问题转化为了两个子问题，merge_sort(left…mid) 和 merge_sort(mid+1…right)，其中下标 mid 等于 left 和 right 的中间位置，也就是 (left+right)/2。当下标从 left 到 mid 和从 mid+1 到 right这两个子数组都排好序之后，我们再将两个有序的子数组合并在一起，这样下标从 left 到 right 之间的数据就也排好序了。

  1. // 归并排序算法, a是数组
  2. static void mergeSort(int[] data) {
  3.     // 申请一个长度等于原数组长度的临时数组,递归分解完数组后，逐层合并时，不用重复申请空间（小优化)
  4.     int[] temp = new int[data.length];
  5.     doMergeSort(data, 0, data.length - 1, temp);
  6. }
  8. // 递归调用函数
  9. static void doMergeSort(int[] data, int left, int right, int[] temp) {
  10.     // 递归终止条件,逐层分解数组，当前分解到只有1个元素时终止递归(左下标与右下标相同)
  11.     if (left >= right) {
  12.          return;
  13.     }
  14.     // 取数组的中间位置下标mid
  15.     int mid = (left + right) / 2;
  16.     // 分治递归
  17.     doMergeSort(data, left, mid, temp); // 左边归并排序，结束后左边序列有序
  18.     doMergeSort(data, mid + 1, right, temp); // 右边归并排序，结束后右边序列有序
  19.     doMerge(data, left, mid, right, temp); // 将左右两边的子序列排序后合并
  20.   }

doMerge() 这个函数的作用就是，将已经有序的 A[left…mid]和 A[mid+1….right]合并成一个有序的数组，并且放入 A[left….right]。那这个过程具体该如何做呢？
合并相邻有序子序列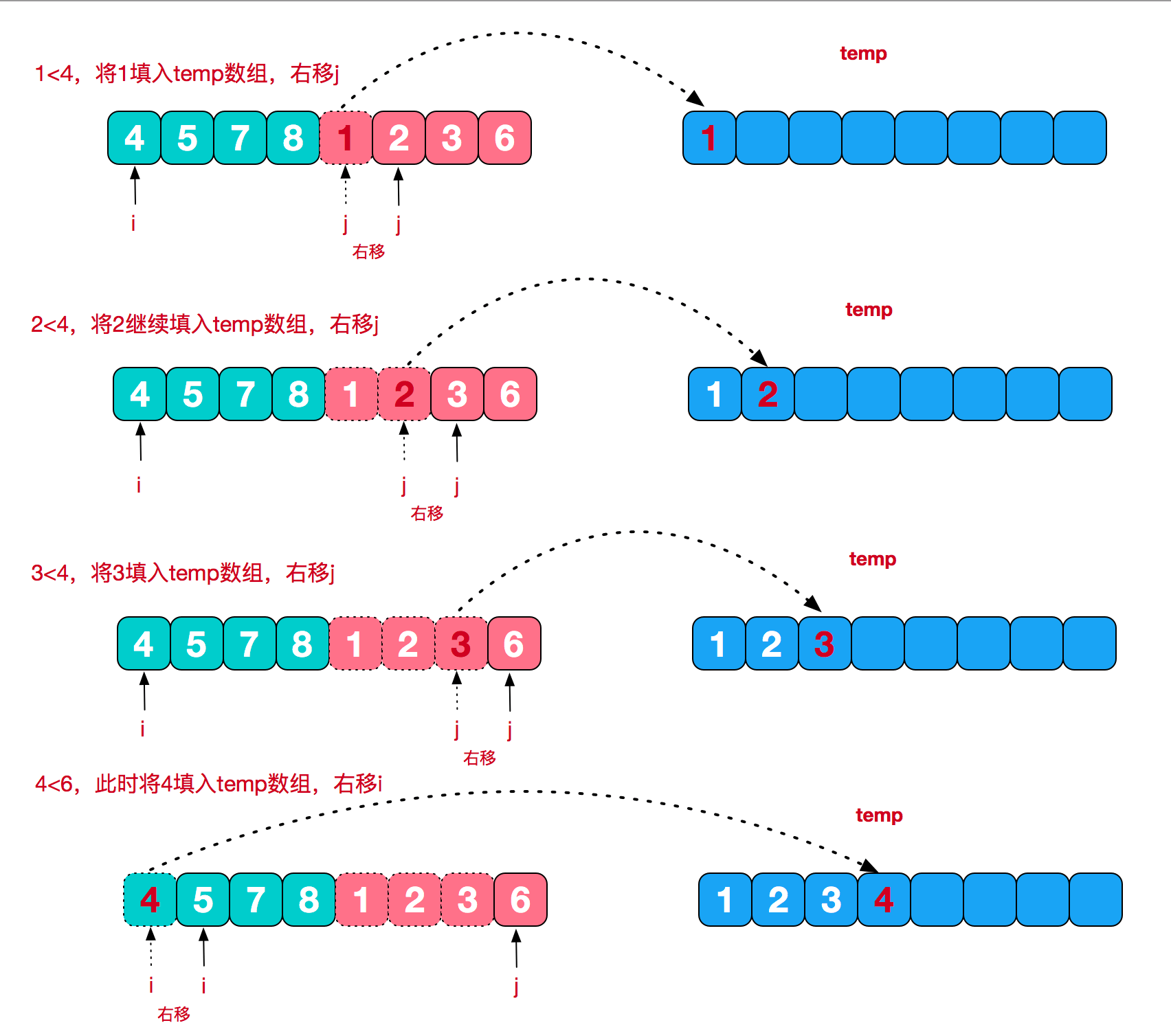
image.png
如图所示，我们申请一个临时数组 temp，大小与 A[left…right]相同。我们用两个游标 i 和 j，分别指向 A[left…mid]和 A[mid+1…right]的第一个元素。比较这两个元素 A[i]和 A[j]，如果 A[i]<=A[j]，我们就把 A[i]放入到临时数组 tmp，并且 i 后移一位，否则将 A[j]放入到数组 tmp，j 后移一位。继续上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾，这个时候，临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[left…right]中。

  1. /**
  2.      * 执行两个子数组的合并
  3.      * 通过递归逐层分解，当拆分数组只有1个元素后，递归结束
  4.      * 推算逻辑从最底层开始返回,此时左右数组序列只有1个元素,首次合并的场景为：
  5.      * 合并2个只有1个元素的数组
  6.      *
  7.      * @param data
  8.      * @param left
  9.      * @param mid
  10.      * @param right
  11.      * @param temp
  12.      */
  13.     static void doMerge(int[] data, int left, int mid, int right, int[] temp) {
  14.         int i = left; // 左序列下标
  15.         int j = mid + 1; // 右序列下标
  16.         int t = 0; // 临时数组下标
  17.         while (i <= mid && j <= right) {
  18.             if (data[i] <= data[j]) {
  19.                 temp[t++] = data[i++]; // t++，i++  先计算当前值，再做自增
  20.             } else {
  21.                 temp[t++] = data[j++];
  22.             }
  23.         }
  24.         // 检查哪个子数组中有剩余的数据
  25.         while (i <= mid) { // 如果i<=mid,表示左边数组还没取完,需要把左边剩余的数据拷贝到临时数组中
  26.             temp[t++] = data[i++];
  27.         }
  28.         while (j <= right) { // 如果j<=right,表示右边数组还没取完,需要把右边剩余的数据拷贝到临时数组中
  29.             temp[t++] = data[j++];
  30.         }
  31.         int k = 0;
  32.         while (left <= right) {
  33.             data[left++] = temp[k++];
  34.         }
  35.     }

当通过递归函数逐层分解到单个元素时，递归结束，此时最开始的合并只会针对单个元素，也就是最先合并【4,8】，具体逻辑则是：比较大小后，放入临时数组，最后拷贝回原数组，也就是原数组的前面2个元素已经排好序，然后继续执行其余的递归逻辑，随着左半边数组递归的退出，数组的左半边已有序，然后后半部的递归退出后，右半部分数组也已有序，最终执行左右部分的子数组排序合并。

说明

1）归并排序是稳定排序算法：在合并的过程中，如果 A[left…mid]和 A[mid+1…right]之间有值相同的元素，那我们可以像代码中那样，先把 A[left…right]中的元素放入 tmp 数组。这样就保证了值相同的元素，在合并前后的先后顺序不变。所以，归并排序是一个稳定的排序算法。
2）归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。
3）尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。

参考

https://www.runoob.com/w3cnote/merge-sort.html