单分类问题

image.png

  • Sigmoid()：将连续分布的值映射成“是”和“否”的回答

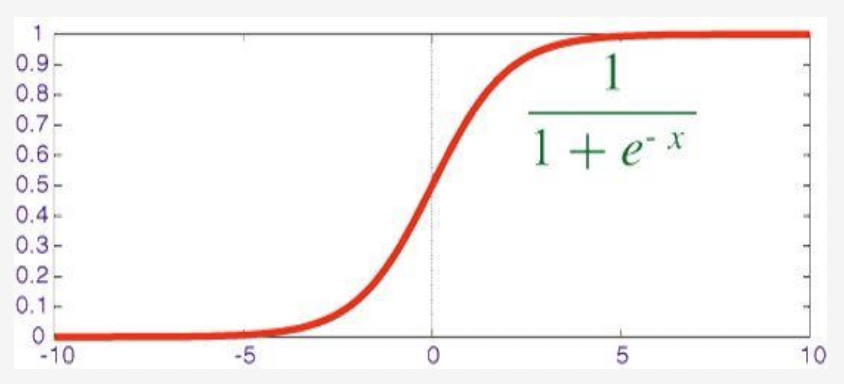
image.png

  • 损失函数：使用交叉熵损失函数。交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。

image.png
在keras里，我们使用 binary_crossentropy 来计算二元交叉熵。

  • 数据预处理

    • 独热编码
      1. x.loc[:, 'Embarked_S'] = (x.Embarked == 'S').astype('int')
      2. x.loc[:, 'Embarked_C'] = (x.Embarked == 'C').astype('int')
      3. x.loc[:, 'Embarked_Q'] = (x.Embarked == 'Q').astype('int')
      4. del x['Embarked'] # 删除原有Embarked列
      5. x
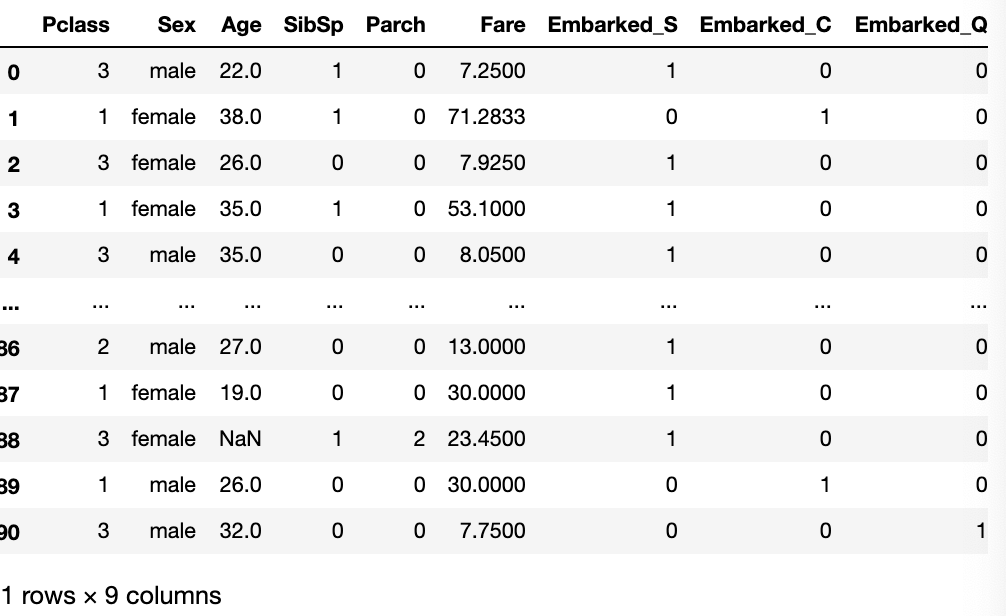
      image.png

  • 建模

    1. model = keras.Sequential() # 初始化顺序模型
    2. from keras import layers
    3. model.add(layers.Dense(1, input_dim=11, activation='sigmoid'))     
    4. #y_pre = (w1*x1 + w2*x2 + ... + w11*x11 + b)
    5. #sigmoid(y_pre) 变成概率值
    6. model.summary()

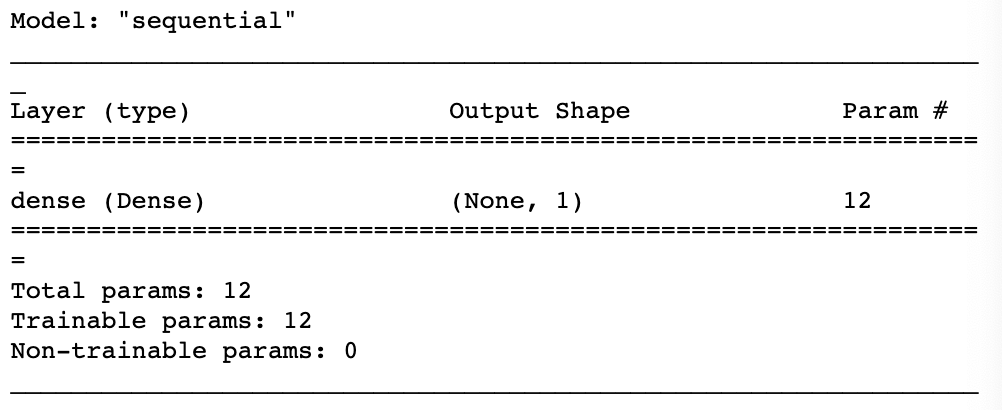
    image.png

  • 编译模型（给模型定义优化算法，以及优化的目标loss ）

    1. # 编译模型：
    2. #  优化函数：adam内置优化算法
    3. #  损失函数：二元交叉熵
    4. #  度量值：acc输出正确率
    5. model.compile(optimizer='adam',
    6.             loss='binary_crossentropy',
    7.             metrics=['acc']
    8. )

  • 训练模型

    1. # 训练模型
    2. history = model.fit(x, y, epochs=300)

  • 测试模型

    1. # 训练中保留的值
    2. history.history.keys()

    image.png

    1. import matplotlib.pyplot as plt
    2. %matplotlib inline
    3. plt.plot(range(300), history.history.get('loss'))

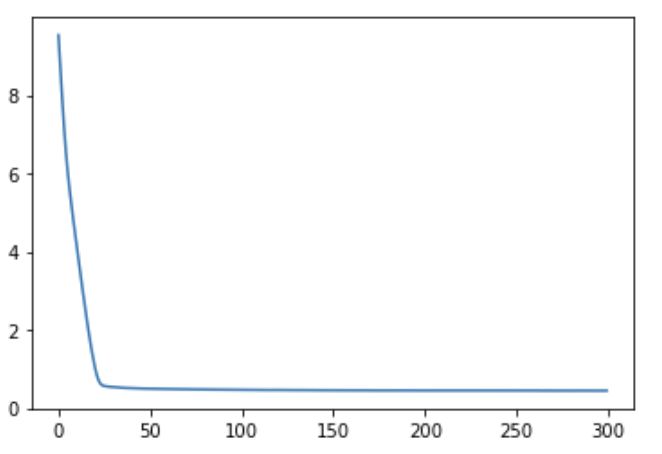
    image.png

    1. plt.plot(range(300), history.history.get('acc'))

    image.png

多分类问题

image.png
image.png
image.png

  • 损失函数：使用softmax交叉熵。

在keras里，对于多分类问题我们使用categorical_crossentropy（独热编码） 和 sparse_categorical_crossentropy（顺序编码）

  • 数据预处理

    • 独热编码

      1. data.Species.unique()

      image.png

      1. # pd.get_dummies()内置函数进行 独热编码
      2. data = data.join(pd.get_dummies(data.Species))
      3. del data['Species']
      4. data

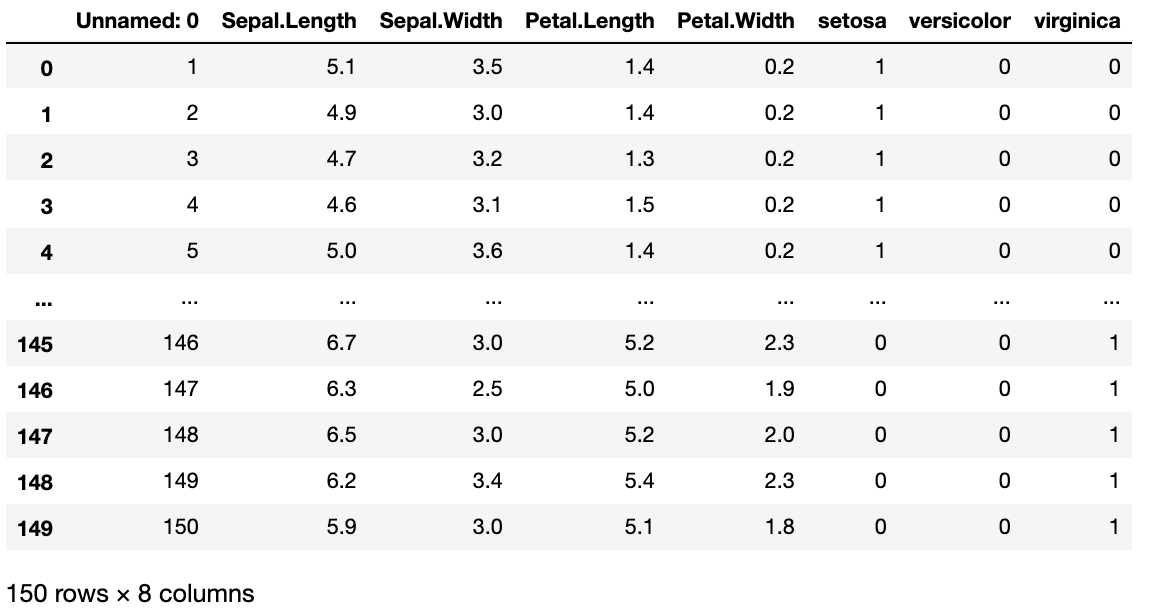
      image.png

      1. # 将data乱序，前面的同种花的数据都排在一起不利于训练
      2. index = np.random.permutation(len(data))
      3. data = data.iloc[index]

    • 顺序编码

      1. data.Species.unique()

      image.png

      1. spc_dic = {'setosa': 0, 'versicolor': 1, 'virginica': 2}
      2. data['Species'] = data.Species.map(spc_dic)
      3. data

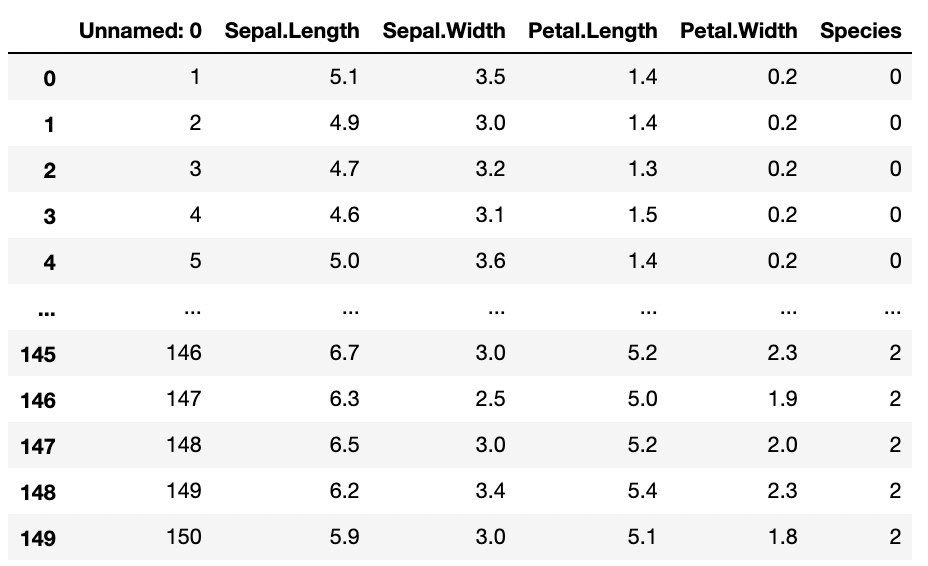
      image.png

  • 建模

    1. # 建立模型
    2. model1 = keras.Sequential()
    3. # 添加Dense层：
    4. #  输出维度：3
    5. #  输入维度：4
    6. #  激活函数：sortmax多分类，将输出值变为概率值 
    7. model1.add(layers.Dense(3, input_dim=4, activation='softmax'))
    8. # 注意这里的参数是15个，思考一下！
    9. model1.summary()

    image.png

  • 编译模型

    • 独热编码

      1. # 编译模型
      2. #  优化函数：adam内置优化算法
      3. #  损失函数：categorical_crossentropy（独热编码适用），来计算softmax交叉熵
      4. #  度量值：acc输出正确率
      5. model1.compile(optimizer='adam',
      6.          loss='categorical_crossentropy', 
      7.          metrics=['acc']
      8. )

    • 顺序编码

      1. # 编译模型
      2. #  优化函数：adam内置优化算法
      3. #  损失函数：sparse_categorical_crossentropy（顺序编码适用），来计算softmax交叉熵
      4. #  度量值：acc输出正确率
      5. model.compile(optimizer='adam',
      6.          loss='sparse_categorical_crossentropy', 
      7.          metrics=['acc']
      8. )

  • 训练模型

    1. # 训练模型
    2. history = model1.fit(x, y, epochs=100)