Regression（回归）

Machine Learning

那所谓的机器学习到底是什么呢？顾名思义，机器他具备有学习的能力，那些科普文章往往把机器学习这个东西吹得玄之又玄好像机器会学习以后，我们就有了人工智慧，有了人工智慧以后机器接下来就要统治人类了。那机器学习到底是什么呢？事实上，机器学习概括来说可以用一句话来描述机器学习这件事，**机器学习就是让机器具备找一个函式的能力**。<br />![](https://cdn.nlark.com/yuque/0/2021/png/1534487/1627460879422-efcc5da2-7689-4f13-ab33-60cfcced31dd.png#height=351&id=yJjRK&originHeight=418&originWidth=530&originalType=binary&ratio=1&size=0&status=done&style=none&width=445)

1. 假设你今天想要叫机器做语音辨识，机器听一段声音，产生这段声音对应的文字，那你需要的就是一个函式，这个函式的输入是声音讯号，输出是这段声音讯号的内容。那你可以想像说 这个可以把声音讯号，当作输入文字当作输出的函式，显然非常非常的复杂，他绝对不是，你可以用人手写出来的方程式，这个函式他非常非常的复杂，人类绝对没有能力把它写出来，所以我们期待凭借着机器的力量，把这个函式自动找出来，这件事情，就是机器学习。
2. 还有好多好多的任务，我们都需要找一个很复杂的函式，举例来说假设我们现在要做，影像辨识。那这个影像辨识，我们需要什么样的函式呢？这个函式的输入是一张图片，他的输出是什么呢？他是这个，图片里面有什么样的内容。
3. 或者是大家都知道的AlphaGo，其实也可以看作是一个函式，要让机器下围棋我们需要的，就是一个函式。这个函式的输入，是棋盘上黑子跟白子的位置，输出是机器下一步，应该落子的位置。假设你可以，找到一个函式。这个函式的输入，就是棋盘上黑子跟白子的位置，输出就是下一步应该落子的位置，那我们就可以让机器做自动下围棋，这件事就可以做一个AlphaGo。

Different types of Functions

1. 随著我们要找的函式不同，机器学习有不同的类别，第一个专有名词，叫作Regression。假设我们今天要找的函式，他的输出是一个数值，他的输出是一个 scalar，那这样子的机器学习的任务，我们称之为Regression。

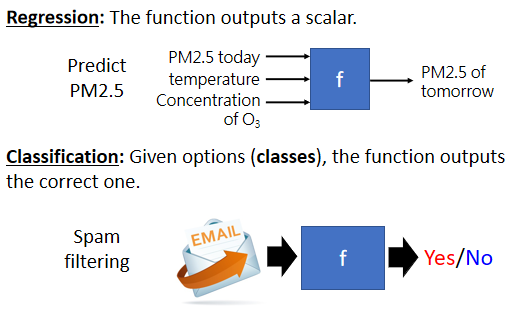
那这边举一个Regression的例子，假设我们今天要机器做的事情，是预测未来某一个时间的，PM2.5的数值。你要叫机器，做的事情是找一个函式，这个我们用f来表示，这个函式的输出，是明天中午的PM2.5的数值，他的输入可能是种种跟预测PM2.5，有关的指数包括今天的PM2.5的数值，今天的平均温度，今天平均的臭氧浓度等等，这一个函式可以拿这些数值当作输入，输出明天中午的PM2.5的数值，那这一个找这个函式的任务，叫作Regression。

1. 除了Regression以外，另外一个大家耳熟能详的任务，叫作Classification，这个任务要机器做的是选择题。我们人类，先准备好一些选项，那这些选项，又叫作类别又叫作classes，我们现在要找的函式它的输出，就是从我们设定好的选项里面，选择一个当作输出那这个问题，这个任务就叫作Classification。

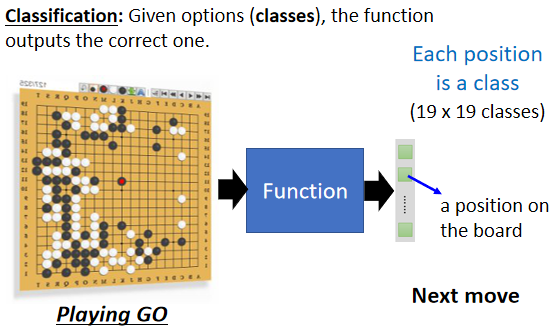
举例来说，现在每个人都有gmail account，那gmail account里面有一个函式，这个函式可以帮我们侦测一封邮件，是不是垃圾邮件，这个函式的输入是一封电子邮件，那他的输出是什么呢，你要先准备好你要机器选的选项，在侦测垃圾邮件这个问题里面，可能的选项就是两个，是垃圾邮件或不是垃圾邮件，Yes或者是No，那机器要从Yes跟No里面，选一个选项出来，这个问题叫作Classification，那Classification不一定只有两个选项，也可以有多个选项 。
举例来说，alpha go本身也是一个Classification的问题，那只是这个Classification，他的选项是比较多的，那如果要叫机器下围棋，你想做一个 alpha go的话，我们要给机器多少的选项呢，你就想想看 棋盘上有多少个位置，那我们知道棋盘上有19乘19个位置，那叫机器下围棋这个问题。其实，就是一个有19乘19个选项的选择题，你要叫机器做的就是找一个函式，这个函式的输入是棋盘上，黑子跟白子的位置，输出就是从19乘19个选项里面，选出一个正确的选项，从19乘19个可以落子的位置里面，选出下一步应该要落子的位置，那这个问题也是一个分类的问题。

⚠️其实很多教科书在讲机器学习的，种种不同类型的任务的时候，往往就讲到这边告诉你说，机器学习两大类任务，一个叫作Regression，一个叫作Classification，然后就结束了，但是假设你对机器学习的认知，只停留在机器学习就是两大类任务，Regression跟Classification，那就好像你以为说，这个世界只有五大洲一样。

你知道这个世界不是只有五大洲，这个世界外面是有一个黑暗大陆的。那在机器学习这个领域里面，所谓的黑暗大陆是什么呢，在于Regression跟Classification以外，大家往往害怕碰触的问题，叫作Structured Learning，也就是机器今天不只是要做选择题，不只是输出一个数字还要产生，一个有结构的物件。举例来说，机器画一张图写一篇文章，这种叫机器产生有结构的东西的问题，就叫作Structured Learning，那如果要讲得比较拟人化，比较潮一点，就是要叫机器学会创造这件事情。

Case Study

我们能不能够根据一个频道过往所有的资讯去预测，它明天有可能的观看的次数是多少呢，我们能不能够找一个函式，这个函式的输入是youtube后台我的资讯，输出就是某一天，隔天这个频道会有的总观看的次数.

机器学习找这个函式的过程，分成三个步骤，那我们就用Youtube频道，点阅人数预测这件事情，来跟大家说明这三个步骤，是怎么运作的。

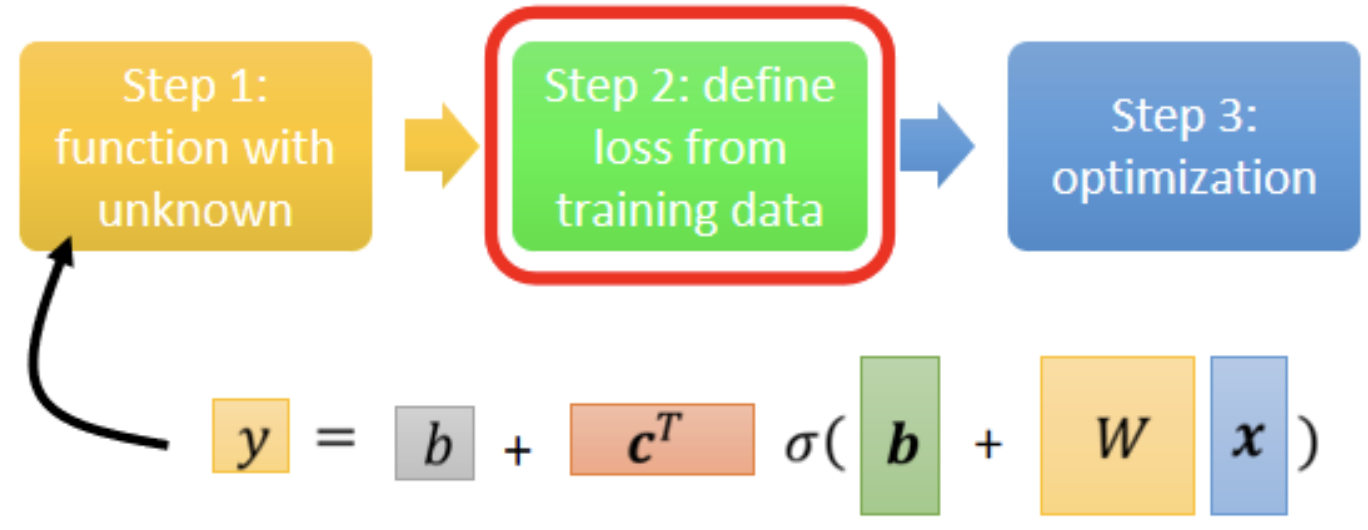
1. Function with Unknown Parameters

第一个步骤是我们要写出一个，带有未知参数的函式。简单来说就是我们先猜测一下这个函式，它的数学式到底长什么样子。举例来说，我们这边先做一个最初步的猜测，我们写成这个样子y=b+w∗xₗ

• y是我们准备要预测的东西，我们准备要预测的是今天这个频道总共观看的人数。
• xₗ是这个频道，前一天总共观看的人数，y跟xₗ都是数值。
• b、w是未知的参数，它是准备要透过资料去找出来的，我们还不知道w跟b应该是多少，我们只是隐约的猜测。

2. Define Loss from Training Data

第二个步骤，是我们要定义一个东西叫做Loss，Loss它也是一个Function，那这个Function它的输入，是我们Model里面的参数，我们的Model叫做y=b+w∗xₗ，而b、w是未知的，是我们准备要找出来的。Loss这个Function输出的值代表说，现在如果我们把这一组未知的参数，设定某一个数值的时候，这笔数值好还是不好。
那这样讲可能你觉得有点抽象，所以我们就举一个具体的例子，假设现在我们给未知的参数的设定是，这bias等于0.5k，这个呢直接等于1，那这个Loss怎么计算呢，如果我们b设0.5k，这个设1，那我们拿来预测，未来的点阅次数的函式 就变成，y等于0.5k加1倍的xₗ，那这样子的一个函式，这个0.5k跟1，他们所代表的这个函式，它有多少呢，这个东西就是Loss.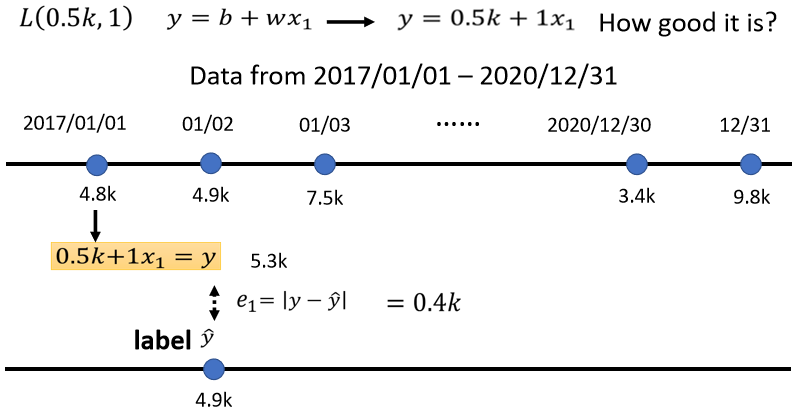




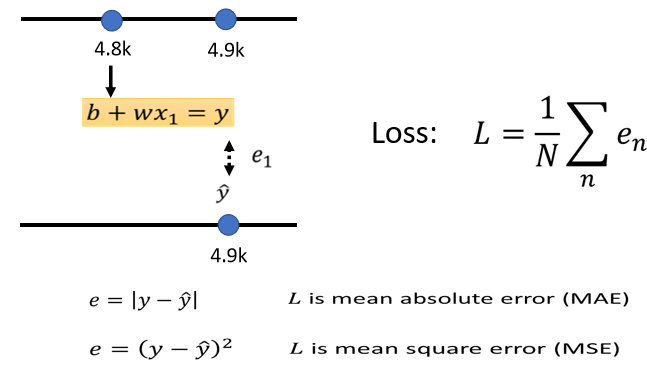
接下来我们就把每一天的误差，通通加起来，加起来然后取得平均，这个N代表我们的训验资料的个数，就是三年来的训练资料，就365乘以3，每年365天所以365乘以3，那我们算出一个L，我们算出一个L，这L是每一笔训练资料的误差，这个e相加以后的结果，这个L就是我们的Loss.L越大，代表我们现在这一组参数越不好，这个L越小，代表现在这一组参数越好。
估测的值跟实际的值之间的差距，其实有不同的计算方法。

• MAE（mean absolute error）：计算y跟ŷ之间绝对值的差距。
• MSE（mean square error）：计算y跟ŷ相减的平方。
• Cross-entropy：如果y和ŷ它都是机率的时候适用。

我们可以调整不同的w，我们可以调整不同的b，求取各种w，求取各种b，组合起来以后，我们可以为不同的w跟b的组合，都去计算它的Loss，然后就可以画出以下这一个等高线图。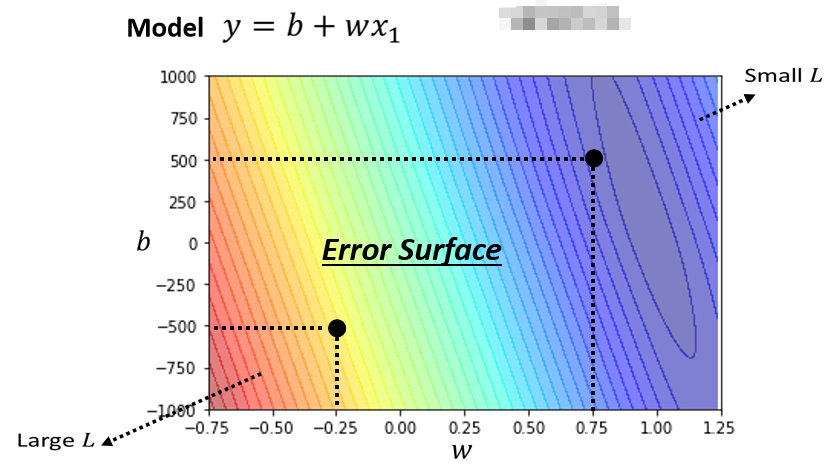

在这个等高线图上面，越偏红色系，代表计算出来的Loss越大，就代表这一组w跟b越差，如果越偏蓝色系，就代表Loss越小，就代表这一组w跟b越好。那像这样子的一个等高线图，就是你试了不同的参数，然后计算它的Loss，画出来的这个等高线图，叫做Error Surface。

3. Optimization

接下来我们进入机器学习的第三步，其实是解一个最佳化的问题，把未知的参数w和b，找一个数值出来，代那一个数值进去，可以让我们的Loss值最小，那个就是我们要找的w和b。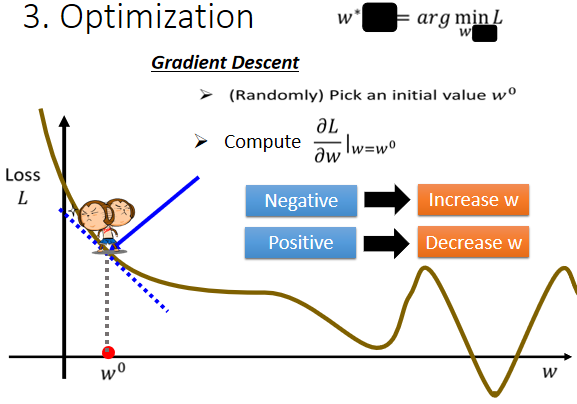

在这一门课里面我们唯一会用到的，Optimization的方法，叫做Gradient Descent。
那当我们w代不同的数值的时候，我们就会得到不同的Loss，这一条曲线就是error surface，只是刚才在前一个例子里面，我们看到的error surface，是二维的是2D的，那这边只有一个参数，所以我们看到的这个error surface，是1D的.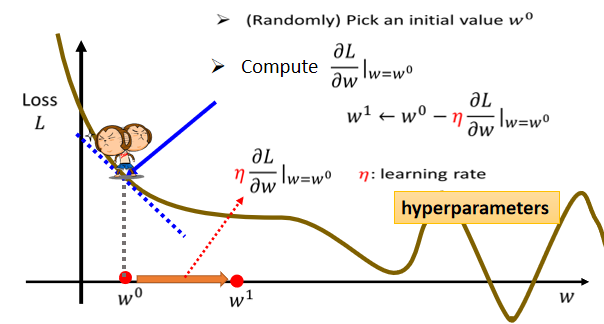

什么时候会停下来呢?

• 第一种状况是你失去耐心了，你一开始会设定说，我今天在调整我的参数的时候，我在计算我的微分的时候，我最多计算几次，那至于要更新几次，这个也是一个hyperparameter，这个是你自己决定的。
• 那还有另外一种理想上的，我们不断调整参数到一个地方，它的微分的值算出来正好是0，所以你的参数就不会再移动位置。

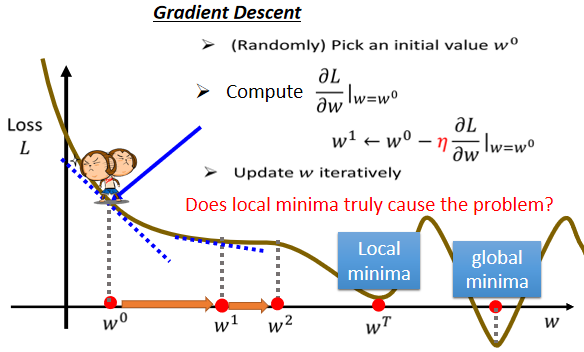
• 常常可能会听到有人讲到，Gradient Descent，不是个好方法，这个方法会有local minima的问题，没有办法真的找到global minima，但这个其实只是幻觉而已，local minima是一个假问题，并不需要我们过分考虑。

Piecewise Linear Curves

所以红色这个线，可以看作是一个常数，再加上一堆蓝色的 Function。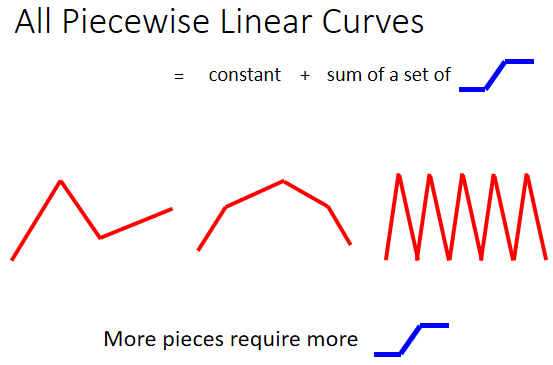

如果Piecewise Linear 的 Curves 越复杂，也就是这个转折的点越多，那需要的这个蓝色的 Function 就越多。
所以我们今天知道一件事情，你可以用 Piecewise Linear 的 Curves，去逼近任何的连续的曲线，而每一个 Piecewise Linear 的 Curves，又都可以用一大堆蓝色的 Function 组合起来，也就是说，我只要有足够的蓝色 Function 把它加起来，我也许就可以变成任何连续的曲线。

这一个蓝色 Function，它的式子应该要怎么把它写出来呢？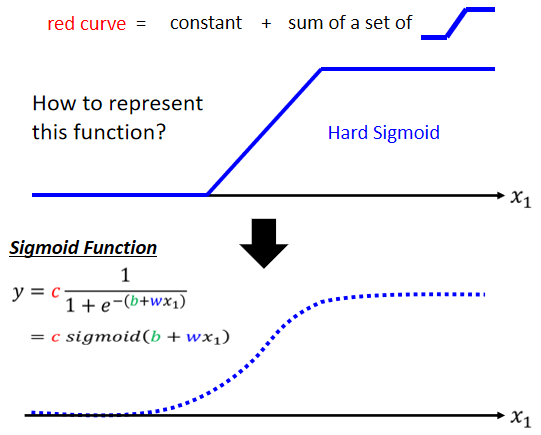

那我们需要各式各样不同的，蓝色的 Function，我们要组出各种不同的曲线，那我们就需要各式各样合适的蓝色的 Function，而这个合适的蓝色的 Function 怎么制造出来呢？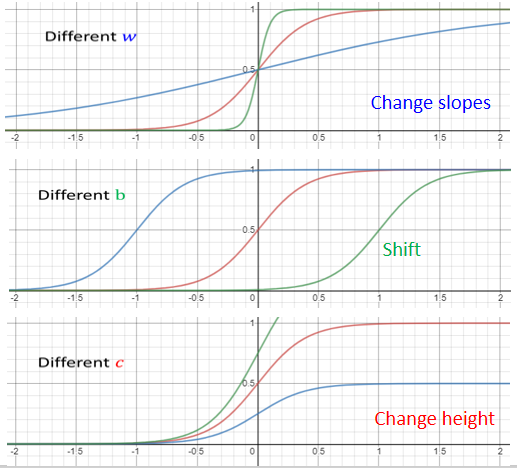

我们就需要调整这里的 b、w、c，你就可以制造各种不同形状的 Sigmoid Function，用各种不同形状的 Sigmoid Function，去逼近这个蓝色的 Function。

• w会改变斜率，改变斜坡的坡度。
• b可以把这一个 Sigmoid Function 左右移动。
• c可以改变它的高度。

所以你只要有不同的 w、b、c，就可以制造出不同的 **Sigmoid Function，把不同的 Sigmoid Function 叠起来以后，你就可以去逼近各种不同的Piecewise Linear 的 Function，然后 Piecewise Linear 的 Function，可以拿来近似各种不同的 Continuous 的 Function。**

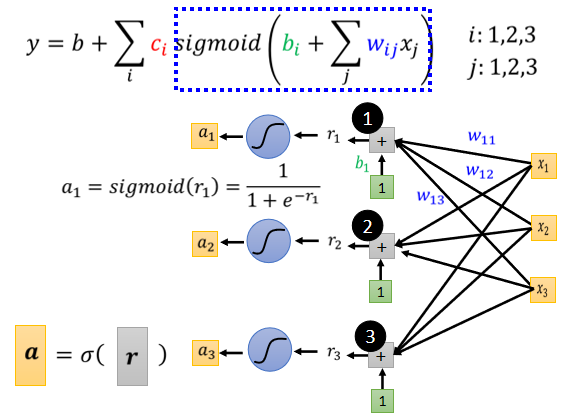
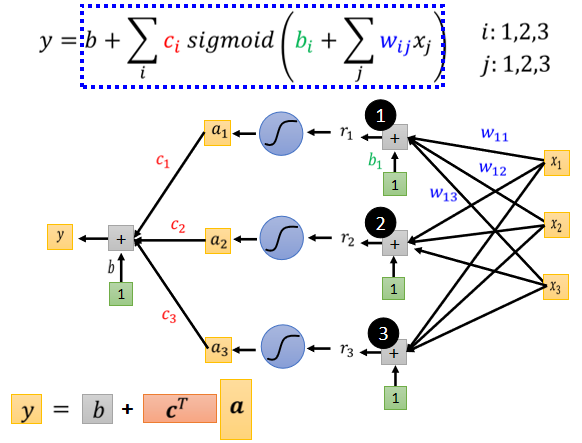
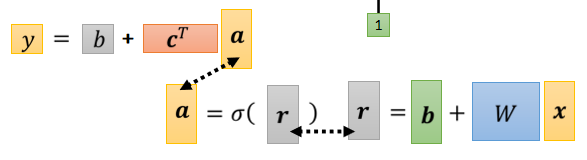
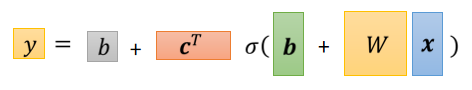
接下来，怎么把这些未知的参数找出来之前，我们先再稍微重新定义一下我们的符号，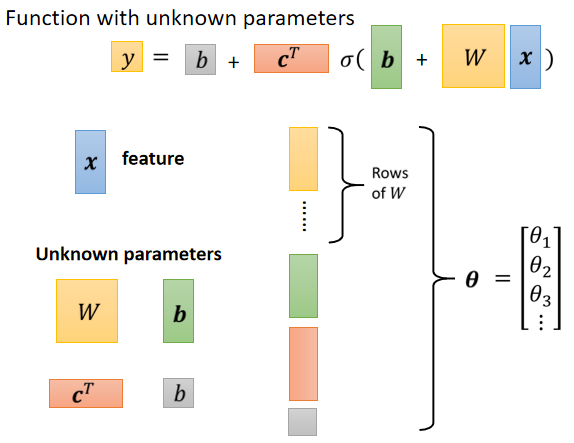

那我们把这些东西通通拉直，拼成一个很长的向量，我们直接用一个符号叫做θ来表示它。这个向量里面有一些数值是来自于这个矩阵，有些数值是来自于b，有些数值来自于c，那我们就不分了，反正它统称为我们所有的未知参数，我们就一律统称θ。

Back to ML

define loss from training data

那接下来进入第二步了，我们要定 Loss，有了新的这个 Model 以后，我们 Loss 没有什么不同，定义的方法是一样的，只是我们的符号改了一下，之前是 L ( w 跟 b )，因為 w 跟 b 是未知的，那我们现在接下来的未知的参数很多了，你再把它一个一个列出来，太累了，所以我们直接用 θ 来统设所有的参数，所以我们现在的 Loss Function 就变成。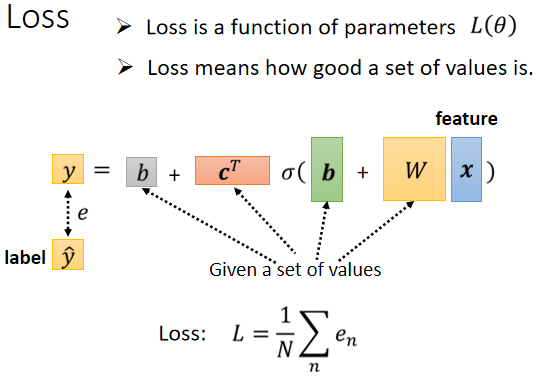

跟刚才只有两个参数的时候，其实是一模一样的。

Optimization

接下来下一步就是 Optimization跟前面讲的没有什么不同。<br />![](https://cdn.nlark.com/yuque/0/2021/png/1534487/1627463878011-34649928-5e76-447e-9e9b-7890f7e11c1e.png#height=344&id=QTtSi&originHeight=390&originWidth=552&originalType=binary&ratio=1&size=0&status=done&style=none&width=487)<br />我们现在的 **θ 它是一个很长的向量**，我们把它表示成 θ1 θ2 θ3……我们现在就是要**找一组 θ，可以让我们的 Loss 越小越好**，可以让 Loss 最小的那一组 θ，我们叫做 θ 的 Start 。

• 我们一开始要随机选一个初始的数值，这边叫做 θ0，我们现在先随机选就好。
• 接下来要计算微分，要对每一个未知的参数（这边用 θ1 θ2 θ3 来表示），都去计算它对 L 的微分，集合起来它就是一个向量，我们用 g 来表示它。这个向量有一个名字叫做 Gradient，把 L 前面放了一个倒三角形，这个就代表了 Gradient。

• 算出这个 g 以后，接下来我们 Update 参数。更新的方法跟刚才只有两个参数的状况是一模一样的。本来有一个参数叫 θ1，上标 0 代表它是一个随机选的起始的值，把这个 θ01减掉 η 乘上微分的值，得到 θ11，代表 θ1 更新过一次的结果，以此类推，就可以把其他参数统统都更新了。

  
  简写把这边所有的 θ 合起来当做一个向量，我们用 θ0来表示，把 η 提出来，那剩下每一个参数对 L 微分的部分，叫做 Gradient 叫做 g，所以 θ0 减掉 η 乘上 g，就得到 θ1。
  

  batch

  
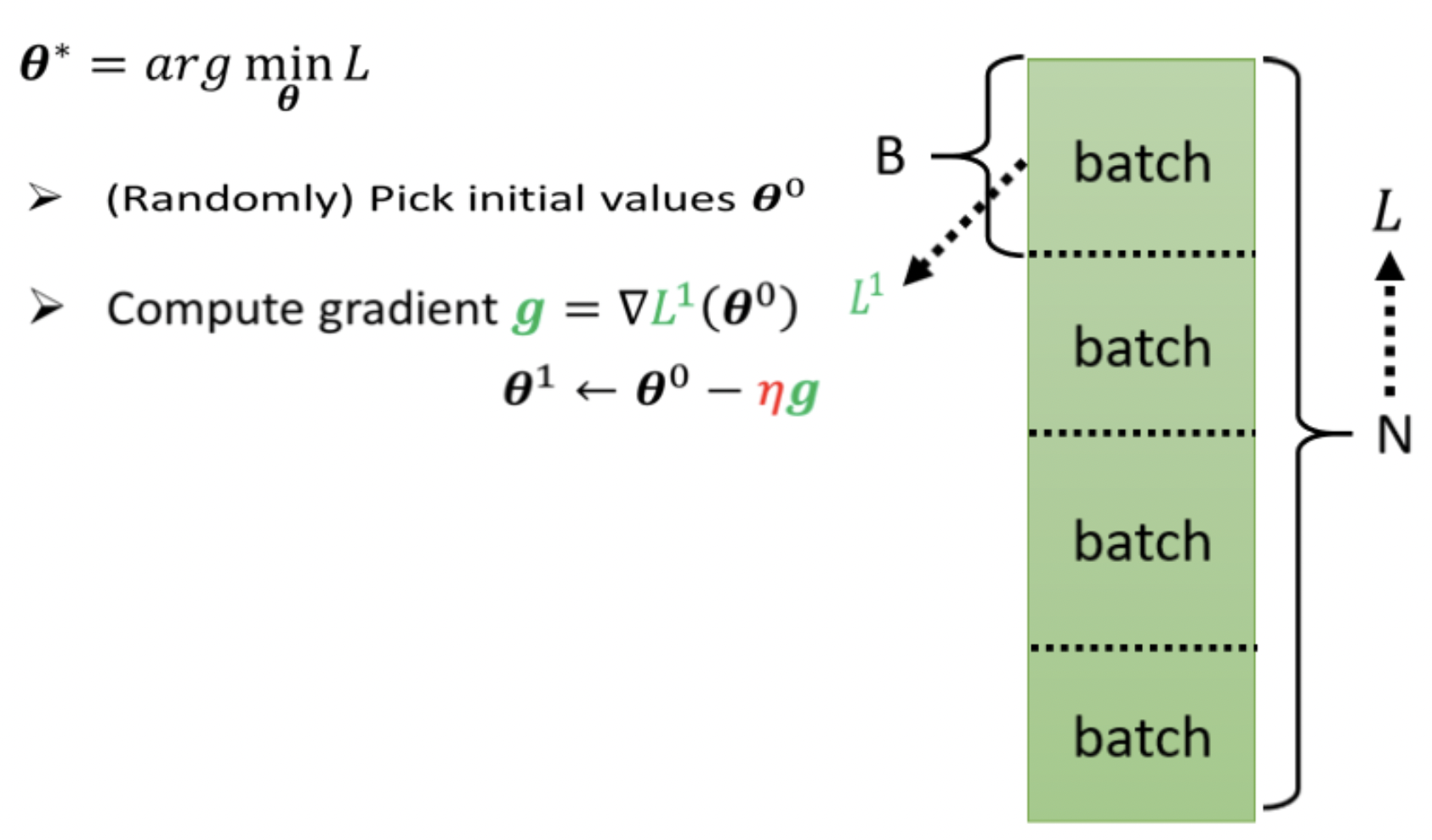
  我们这边有大 N 笔资料，我们会把这大 N 笔资料随机分成一个一个的 Batch。
  那本来我们是把所有的 Data 拿出来算一个 Loss，那现在我们只拿一个 Batch 里面的 Data出来算一个 Loss，我们这边把它叫 L1。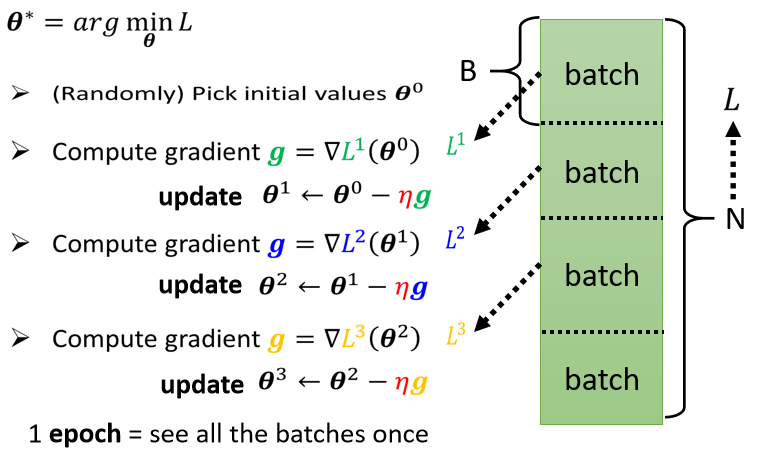
  
  但是你可以想像说假设这个 B 够大，也许 L 跟 L1 会很接近也说不定。所以实际上，每次我们会先选一个 Batch，用这个 Batch 来算 L1，根据这个 L1 来算 Gradient，用这个 Gradient 来更新参数，接下来再选下一个 Batch 算出 L2，根据 L2 算出 Gradient，然后再更新参数，再取下一个 Batch 算出 L3，根据 L3 算出 Gradient，再用 L3 算出来的 Gradient 来更新参数……
  所以我们并不是拿大 L 来算 Gradient，实际上我们是拿一个 Batch 算出来的 L1 L2 L3…，来计算 Gradient。那把所有的 Batch 都看过一次，叫做一个 **Epoch，每一次更新参数叫做**一次 Update， Update 跟 Epoch 是不一样的东西。
  
  所以做了一个 Epoch 的训练，你其实不知道它更新了几次参数，有可能 1000 次，也有可能 10 次，取决于它的 Batch Size 有多大。

  模型变型

  那我们其实还可以对模型做更多的变形，你确实可以不一定要换成 Soft 的 Sigmoid，有其他的做法，举例来说这个 Hard 的 Sigmoid，它可以看作是两个 Rectified Linear Unit 的加总。
  
  每条不同的 w b c，你就可以挪动它的位置，改变这条线的斜率，那这种线在机器学习里面，我们叫做 Rectified Linear Unit，它的缩写叫做 ReLU。
  
  那你把两个 ReLU 叠起来，就可以变成 Hard 的 Sigmoid，你想要用 ReLU 的话，就把 Sigmoid 的地方，换成。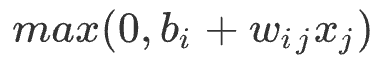
  你要 2 个 ReLU，才能够合成一个 Hard Sigmoid。表示那个蓝色的 Function 不是只有一种做法，你完全可以用其他的做法，这个 Sigmoid 或是 ReLU在机器学习里面，我们就叫它 Activation Function。

  好名字

  那我们现在还缺了一个东西，缺一个好名字，这些 Sigmoid 或 ReLU ，它们叫做 Neuron，我们这边有很多的 Neuron，很多的 Neuron 就叫做 Neural Network，Neuron 就是神经元（其实和人脑的神经元没有一点关系）。
  
  从Neural Network到Deep Learning就是起名字的艺术！