Optimization with Batch

实际上在算微分的时候，并不是真的对所有 Data 算出来的 L 作微分。你是把所有的 Data 分成一个一个的 Batch（有的人是叫Mini Batch ）。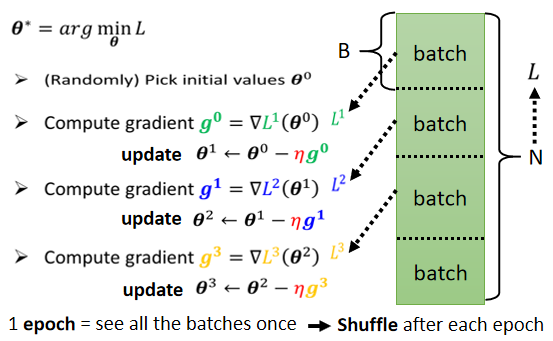
image.png
每一个 Batch 的大小呢，就是大B一笔的资料。我们每次在 Update 参数的时候，我们是拿大B一笔资料出来，算个 Loss，算个 Gradient，Update 参数；再拿另外B一笔资料，再算个 Loss，再算个 Gradient，再 Update 参数，以此类推。所以我们不会拿所有的资料一起去算出Loss，我们只会拿一个 Batch 的资料去算Loss。
在做这些 Batch 的时候，你会做一件事情叫做 Shuffle。一个常见的做法就是，在每一个 Epoch 开始之前，会分一次 Batch，然后每一个 Epoch 的 Batch 都不一样。

Small Batch v.s. Large Batch

image.png
我们来比较左右两边这两个最极端状况的 Case，那假设现在我们有20笔训练资料。

  • 左边的 Case 就是没有用 Batch，Batch Size直接设的跟训练资料一样多，这种状况叫做 Full Batch。
  • 右边的 Case 就是Batch Size 等于1。

在左边 Case 里面，我们必须要把所有20笔 Examples 都看完以后，我们的参数才能够 Update 一次。
在右边 Case 里面，如果今天总共有20笔资料的话，那在每一个 Epoch 里面，我们的参数会 Update 20次。所以我们今天 Update 的方向，你会发现它是曲曲折折的。

运算时间比较

实际上考虑并行运算的话，左边这个并不一定时间比较长。
GPU 虽然有平行运算的能力，但它平行运算能力终究是有个极限，所以你 Batch Size 真的很大的时候，时间还是会增加的。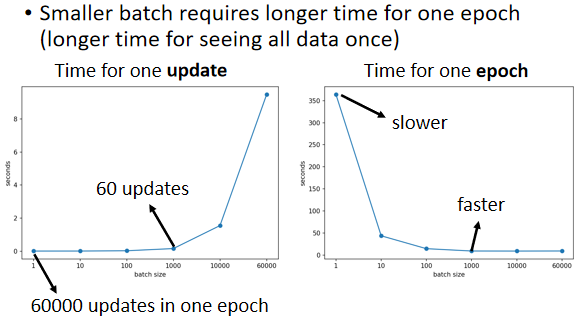
image.png
但是因为有平行运算的能力，实际上当你的 Batch Size 小的时候，你要跑完一个 Epoch，花的时间是比大的 Batch Size 还要多。

模型训练结果比较

如果你今天拿不同的 Batch 来训练你的模型，你可能会得到这样子的结果，左边是在 MNIST 上，右边是在 CIFAR-10 上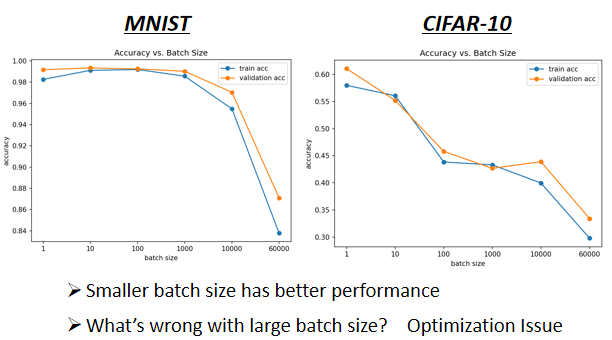
image.png
横轴代表的是 Batch Size，从左到右越来越大。纵轴代表的是正确率，越上面正确率越高，当然正确率越高越好。
神奇的事情是，大的 Batch Size，往往在 Training 的时候，会给你带来比较差的结果（尚待研究的问题）。

那这边就是比较了一下，大的 Batch 和小的 Batch。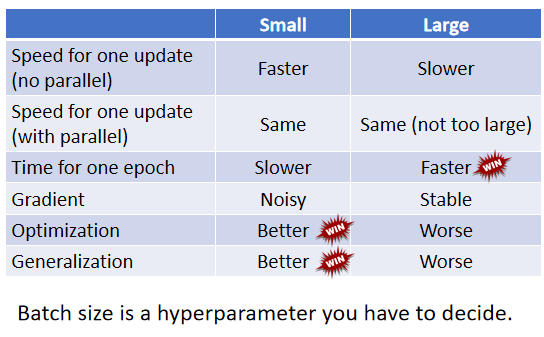
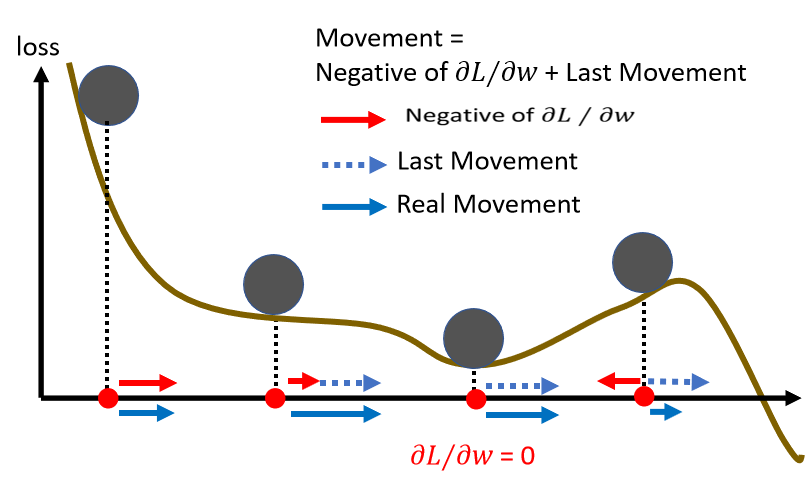
image.png

Momentum

Momentum动量，这也是另外一个有可能可以对抗 Saddle Point和Local Minima 的技术。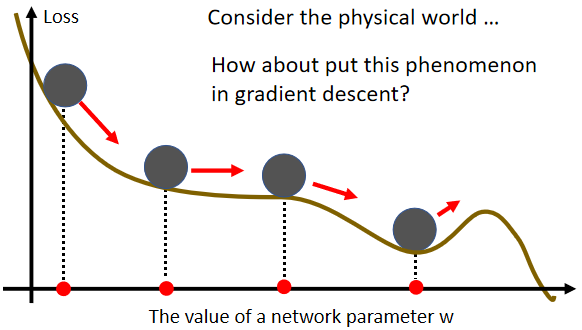
image.png
它的概念，你可以想像成在物理的世界里面，假设 Error Surface 就是真正的斜坡，而我们的参数是一个球，你把球从斜坡上滚下来，如果今天是 Gradient Descent，它走到 Local Minima 或 Saddle Point 就停住了。
但是在物理的世界里，一个球如果从高处滚下来，如果有惯性，就算滚到 Saddle Point 或 Local Minima，如果它的动量够大的话，它还是会继续往右走，甚至翻过这个小坡然后继续往右走。
当加上 Momentum 的时候，我们 Update 的方向，不是只考虑现在的 Gradient，而是考虑过去所有 Gradient 的总和。image.png