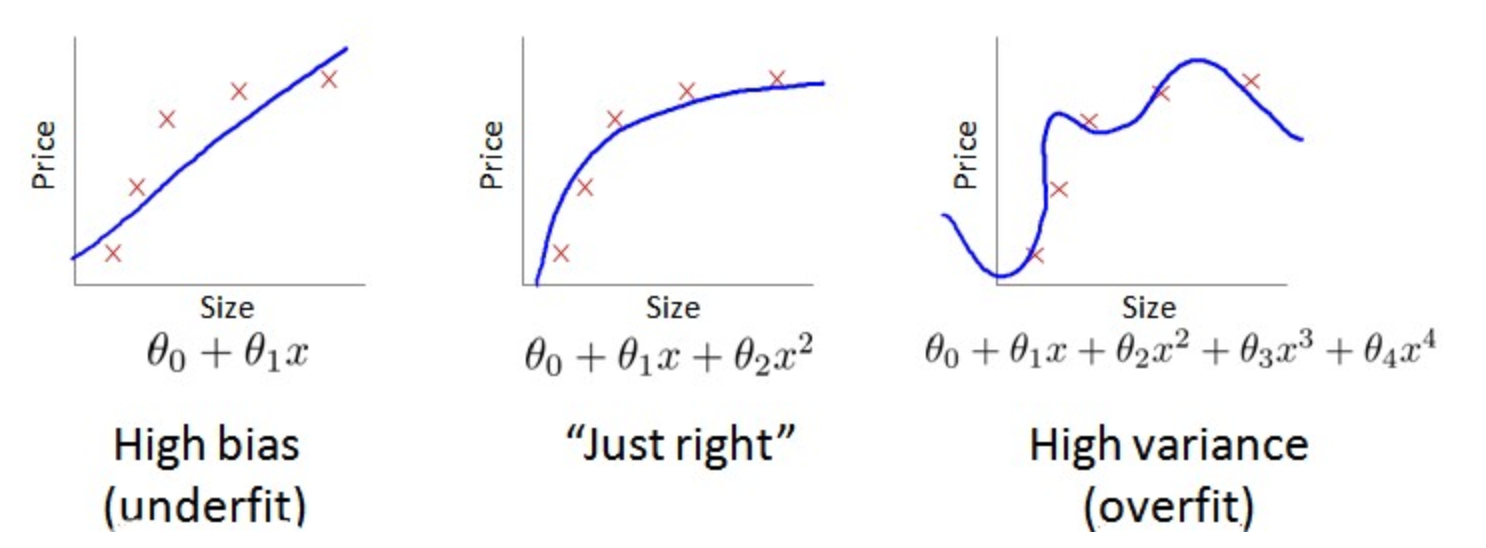
1. 模型选择
用测试集来选择合适的多项式模型后,仍用测试集来计算模型泛化误差,是不太可取的,如果你的数据集很大还勉强可以,但是最好的做法是:
- 用训练集训练模型
- 用(交叉)验证集选择模型
- 最后用测试集来计算误差(将这个误差看作是理想的对于新样本的泛化误差)
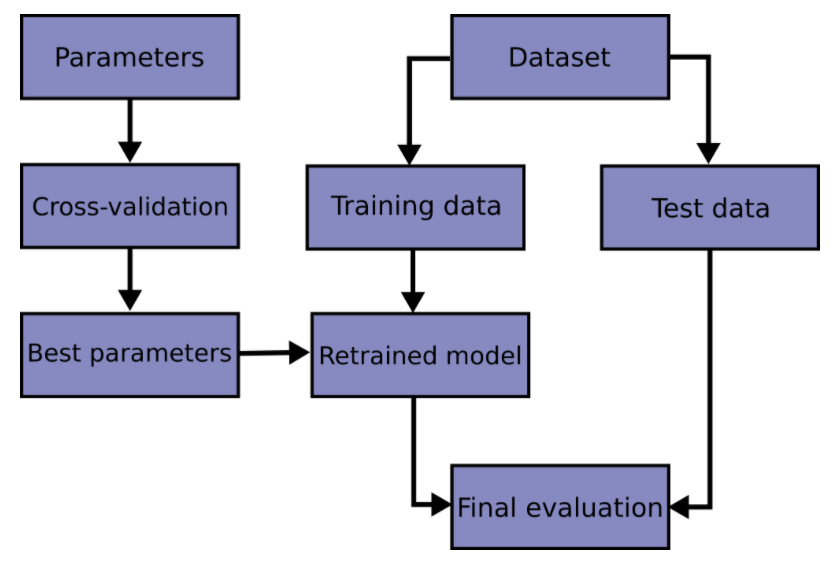
三种集合的划分比例一般为3:1:1。当然在验证集划分训练的时候还有一些小trick,因为我们的模型结果会很大程度上取决于训练集和验证集的划分情况,所以为解决这一问题,我们可以采用交叉验证(cross-validation)这一流程。
1.1 留一交叉验证(LOOCV, Leave-one-out cross-validation)
只用其中一个数据做为交叉验证集,其他全部数据作为训练集,重复N次。
1.2 K折交叉验证(K-fold Cross Validation)
把数据集分成K份,取其中的一份为验证集,其他部分为训练集,重复K次。
K的选取是一个Bias和Variance的trade-off。一般选为5/10。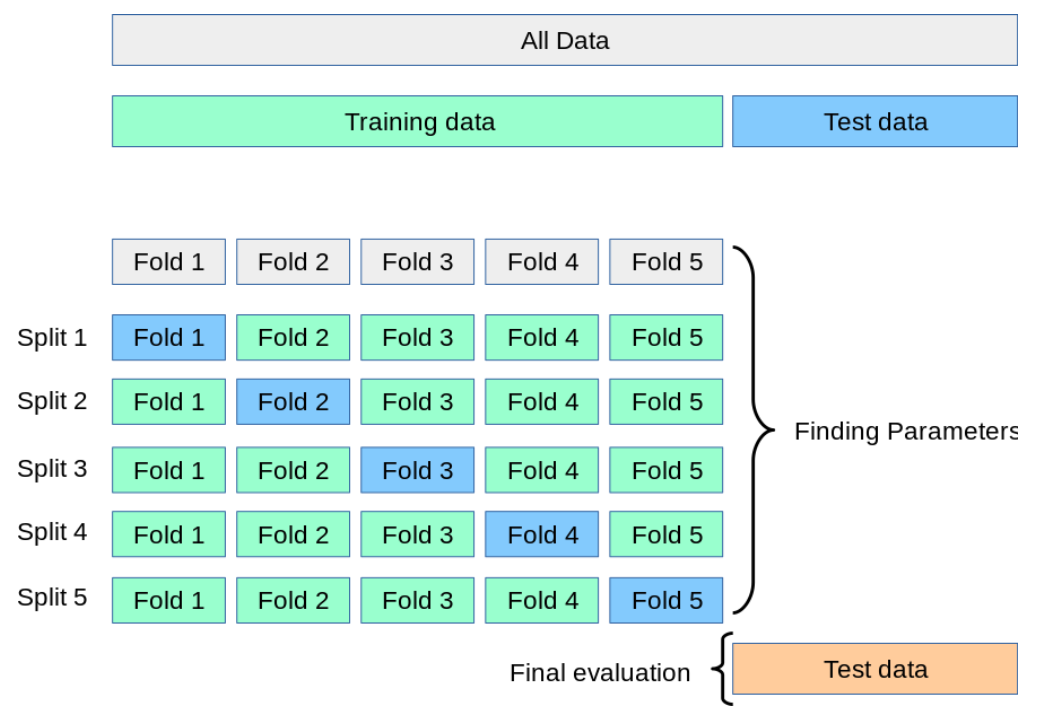
这种做法可能会耗费一些算力,所以在数据集较小的情况下,优势更明显。
2. 模型诊断
2.1 偏/方差的基本概念
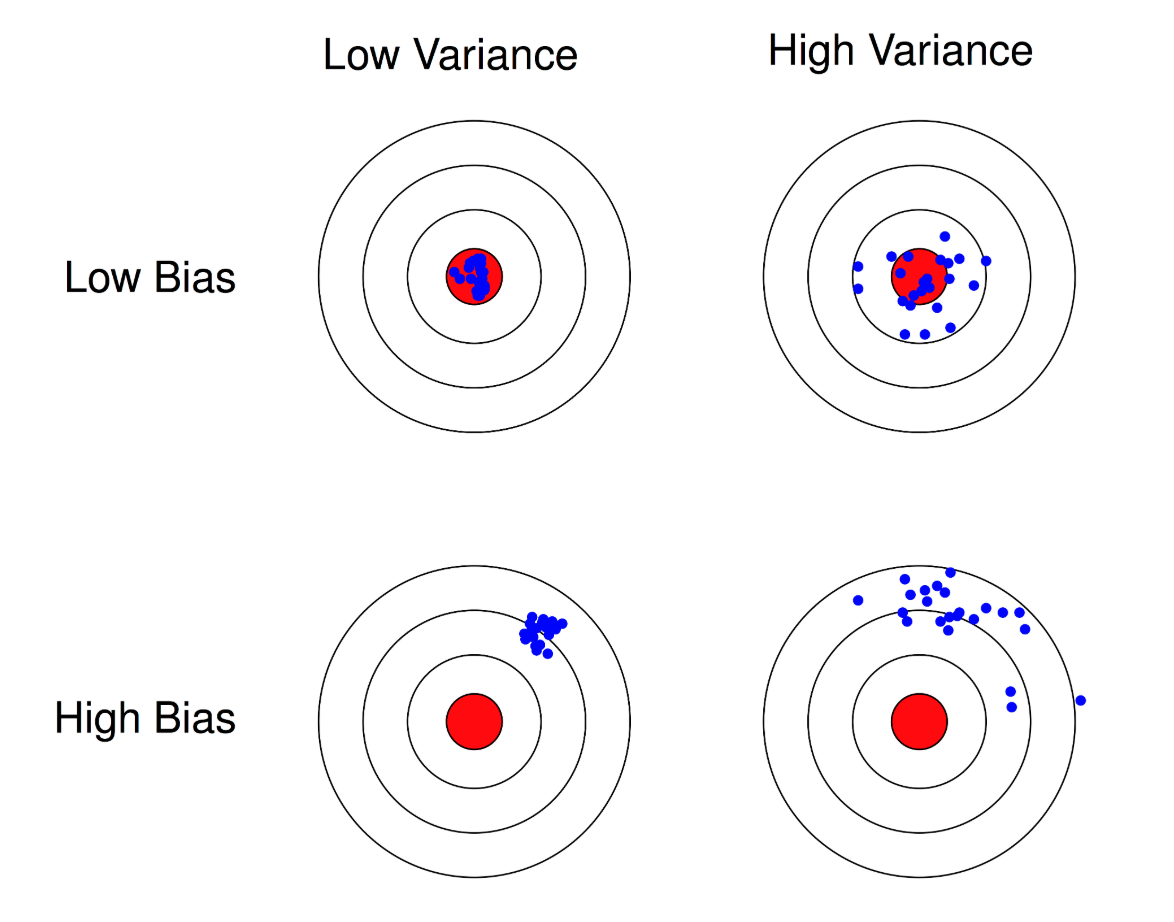
偏差(bias)
- 偏差,即预测值与真实值的差值(偏离程度)。
- 若模型有较高的偏差,我们常称为模型欠拟合(underfit)。
方差(variance)
- 方差,即随机变量在其期望值附近的波动程度,它衡量了模型的抗干扰能力,即泛化能力。
- 模型有较高的方差,我们常称为模型过拟合(overfit)。
2.2 正则化与偏/方差的关系
在我们在训练模型的过程中,一般会使用一些正则化方法来防止过拟合,但是往往正则化参数过大或者过小也会对模型产生影响: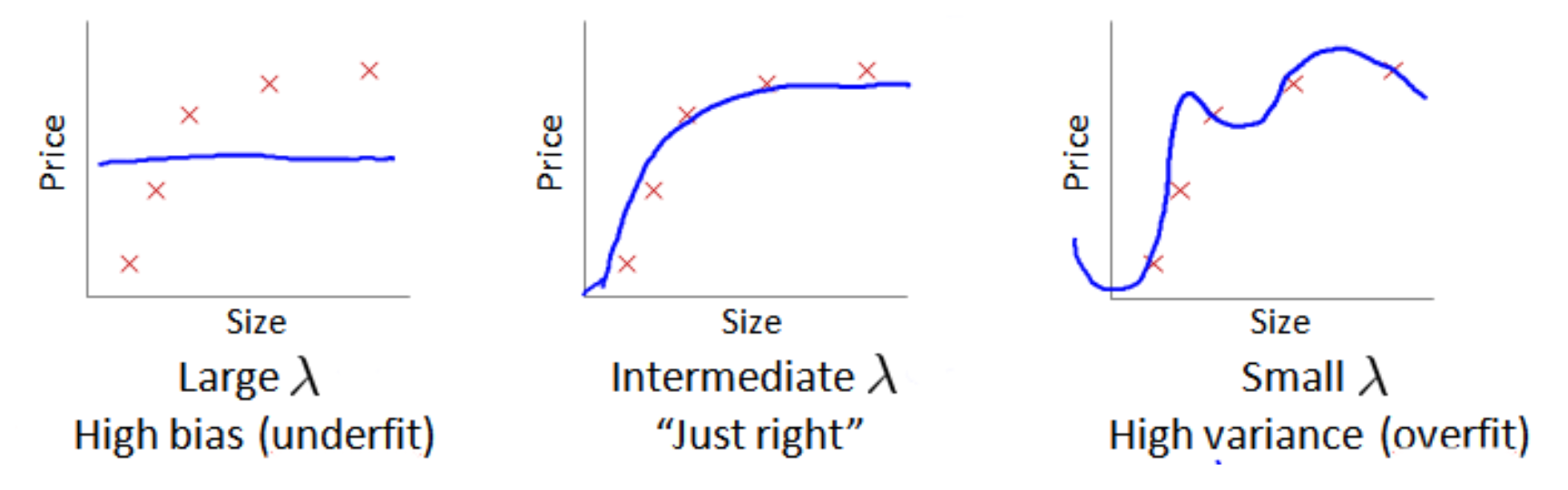

当
较小时,训练集误差较小(过拟合)而交叉验证集误差较大,随着
的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加。
2.3 利用学习曲线诊断模型
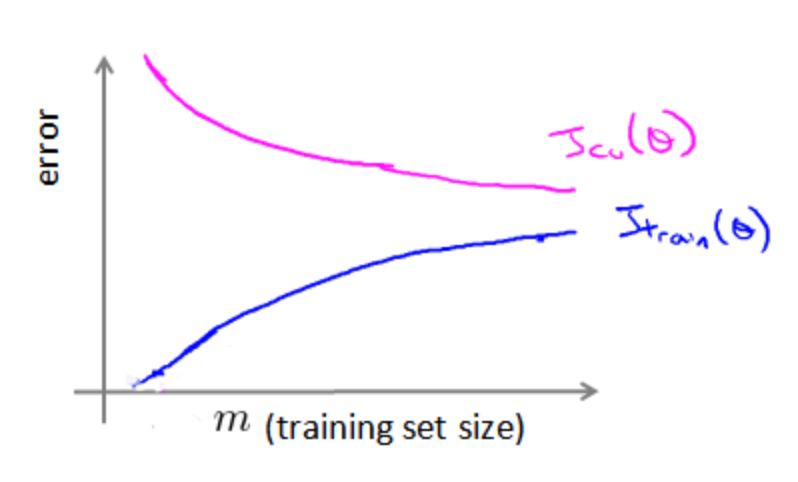
学习曲线就是一种很好的工具,我经常使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。学习曲线是学习算法的一个很好的合理检验(sanity check)。学习曲线是将训练集误差和交叉验证集误差作为训练集样本数量
的函数绘制的图表。 即,如果我们有100行数据,我们从1行数据开始,逐渐学习更多行的数据。思想是:当训练较少行数据的时候,训练的模型将能够非常完美地适应较少的训练数据,但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。
2.4 解决高偏/方差方法
高偏差(欠拟合)解决方法:
- 尝试获得更多的特征。
- 尝试增加多项式特征。
- 尝试减少正则化程度
。
高方差(过拟合)解决方法:
- 尝试增大数据集。训练的数据量太小或者训练数据占总数据的比例过小会导致模型过拟合,这时候就要进行数据扩充。
- 尝试减少特征的数量。
- 尝试增加正则化程度
。
- 采用集成模型。Bagging,Boosting等将多个弱学习器Bagging 一下效果会好很多,比如随机森林等。具体可以参考我的另一篇文章。
DNN中常用解决方法:
- 采用dropout方法。dropout方法是ImageNet中提出的一种方法,通俗一点讲就是dropout方法在训练的时候让神经元以一定的概率不工作。
- 早停策略。本质上是交叉验证策略,选择合适的训练次数,避免训练的网络过度拟合训练数据。
- BN。BN主要针对梯度弥散和数据分布不一致的问题,但原论文中也提到其能起到和dropout相同的正则化作用。具体可以参考我的另一篇文章。
3. 模型误差分析
3.1 回归模型评价指标
3.1.1 均方误差(Mean Squared Error,MSE)
观测值与真值偏差的平方和与观测次数的比值: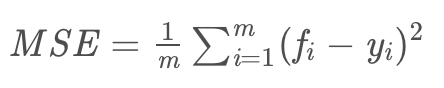
这就是线性回归中最常用的损失函数,线性回归过程中尽量让该损失函数最小。那么模型之间的对比也可以用它来比较。MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
3.1.2 均方根误差/标准误差(Root Mean Squard Error,RMSE)
标准差是方差的算术平方根;标准误差是均方误差的算术平方根。
标准差是用来衡量一组数自身的离散程度;而均方根误差是用来衡量观测值同真值之间的偏差。它们的研究对象和研究目的不同,但是计算过程类似。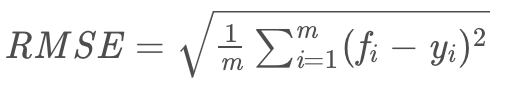
它的意义在于开个根号后,误差的结果就与数据是一个级别的,可以更好地来描述数据。标准误差对一组测量中的特大或特小误差反映非常敏感,所以,标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。
3.1.3 平均绝对误差(Mean Absolute Error,MAE)
平均绝对误差是绝对误差的平均值,平均绝对误差能更好地反映预测值误差的实际情况: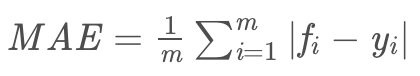
3.1.4 R-squared
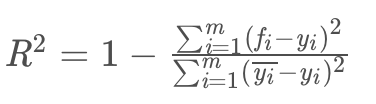
分子为模型预测的平方误差,分母为观测平均值的平方误差。如果结果是0,就说明我们的模型跟随机猜测差不多。
如果结果是1,就说明我们模型无错误。R^2介于0~1之间,越接近1,回归拟合效果越好,一般认为超过0.8的模型拟合优度比较高。
化简上面的公式,分子分母同时除以m,那么分子就变成了我们的均方误差MSE,下面分母就变成了方差。 
3.2 分类模型评价指标
3.2.1 accuracy、precison、recall(中文三个词实在太拗口,直接采用英文原词)、F值
先来个简单粗暴易懂的解释:
- 召回率:正样本有多少被预测对了(找出来),即召回了多少;
- 精确率:你认为的正样本,有多少猜对了(猜的精确性如何)。
由于偏斜类的存在,我们并不能直接通过算法的误差率来衡量算法效果。
以预测肿瘤良性/恶心为例,实际样本中,恶性肿瘤占比为0.5%,良性为99.5%,我们要用一个算法来预测肿瘤的良性/恶性情况。此时有两个算法模型:A.神经网络模型 B.一个错误的模型 在B模型中,每次预测都判断为良性,则对于真实样本来看,其误差在0.5%;A模型经过正常训练的神经网络模型,误差在1%,那么我们就不能仅仅依靠数字来比较算法模型的准确性。因为明显地B是一个错误的模型。
混淆矩阵: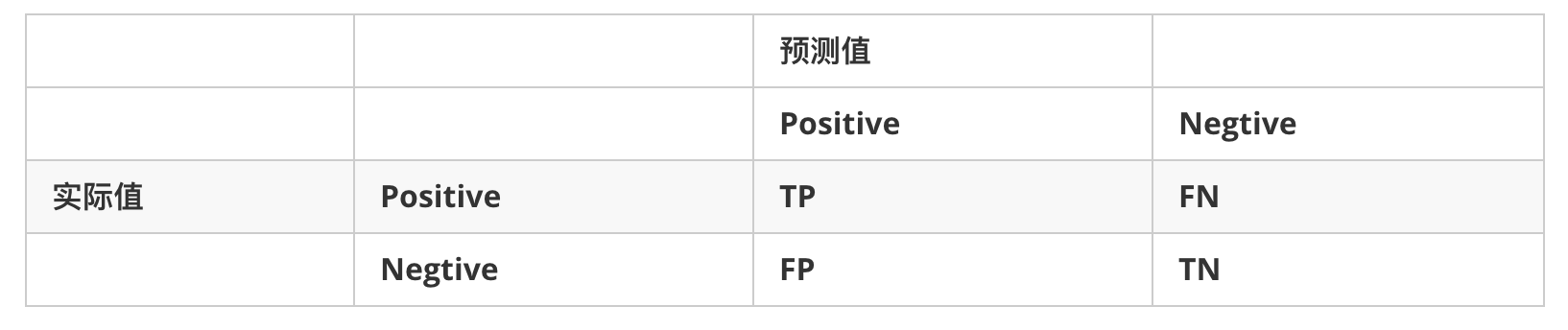
precision=TP/(TP+FP),即代表所有预测为正的样本中预测对的比例。
recall=TP/(TP+FN),即代表所有原本为正的样本中预测对的比例。
有时候单一的P或R并不能代表算法的效果,P和R的关系如下图所示: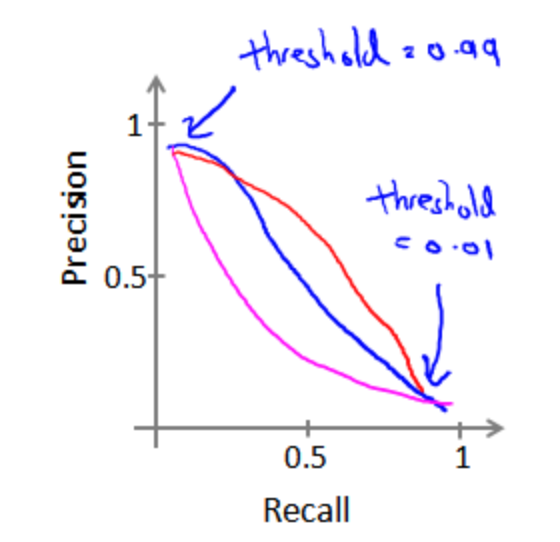
这时候我们要把他们综合考量:F1=2PR/(P+R),即代表P和R的调和平均值
有时候利用算术平均数无法理想的衡量出相关指标时,我们可以用调和平均数来进行改进(典型的统计学中的F值就是P和R的调和平均)。
三种F值计算方法:
micro-F1(微平均): “Micro”是通过先计算总体的TP, FP和FN的数量,然后计算PRF。即先将多个混淆矩阵的TP,FP,TN,FN对应的位置求平均,然后按照PRF值公式进行计算。
macro-F1(宏平均): “Macro”是分别计算每个类别的PRF,然后分别求平均得到PRF。即对多个混淆矩阵求PRF,然后求PRF的算术平均。
weighted-F1:weighted计算方法就是对于macro中的每一类的PRF给予不同的权重(在sklearn中是按样本数目加权平均每一类的F1)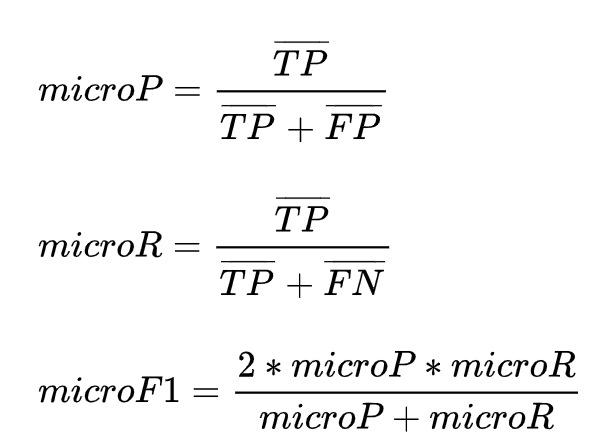
3.2.2 ROC曲线和AUC面积
ROC曲线:接收者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,roc曲线上每个点反映着对同一信号刺激的感受性。
ROC曲线上每个点对应一个分类选取的阈值。 横轴代表实际为负的样本中预测错误的比例。 纵轴代表实际为正的样本中预测正确的比例,即recall。
在一个二分类模型中,假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如0.6,概率大于等于0.6的为正类,小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。
AUC,即ROC曲线的下面积,它能够将ROC曲线衡量的效果量化,所以我们可以直接根据AUC大小来判断分类器的性能。
4. 大规模机器学习
4.1 批量梯度下降、随机梯度下降、mini-batch梯度下降
如果我们的训练集很大是,我们可以尝试使用随机梯度下降法来代替批量梯度下降法,SGD每次只根据单个样本的损失函数计算梯度来更新参数,注意运行SGD之前对数据进行shuffle来实现stochastic机制。
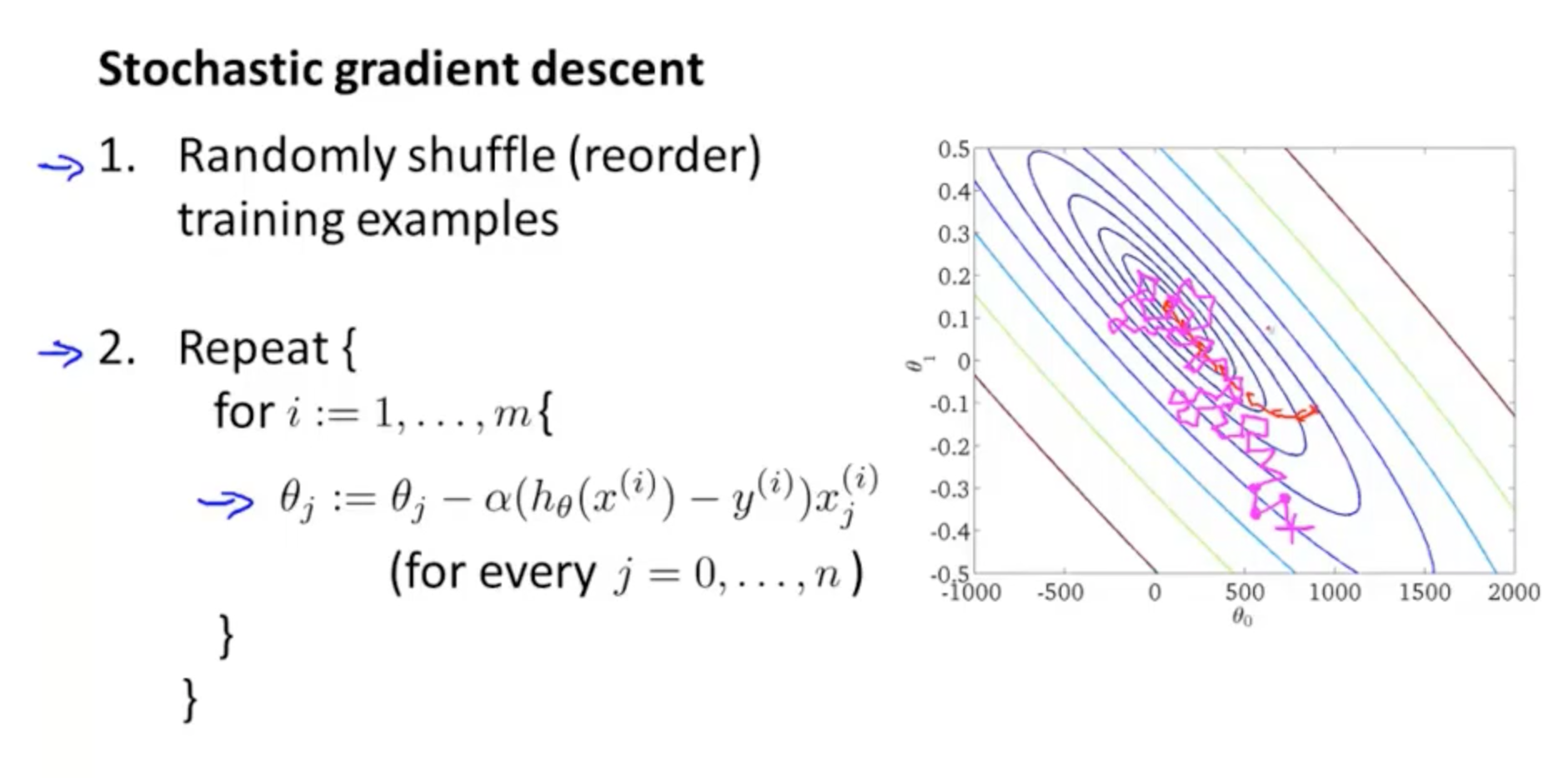
随机梯度下降算法在每一次计算之后便更新参数 ,而不需要首先将所有的训练集求和,在梯度下降算法还没有完成一次迭代时,随机梯度下降算法便已经走出了很远。但是这样的算法存在的问题是,不是每一步都是朝着”正确”的方向迈出的。因此算法虽然会逐渐走向全局最小值的位置,但是可能无法站到那个最小值的那一点,而是在最小值点附近徘徊。
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数b次训练实例,便更新一次参数
通常我们会令 在 2-100 之间。这样做的好处在于,我们可以用向量化的方式来循环 个训练实例,如果我们用的线性代数函数库比较好,能够支持平行处理,那么算法的总体表现将不受影响(甚至由于SGD)。
4.2 在线学习
即无需固定存储一个数据集,而是根据连续的数据流不断的调整算法模型的参数。
4.3 并行化操作
如果任何学习算法能够表达为,对训练集的函数的求和,那么便能将这个任务分配给多台计算机(或者同一台计算机的不同CPU 核心),以达到加速处理的目的。
例如,我们有400个训练实例,我们可以将批量梯度下降的求和任务分配给4台计算机进行处理:
很多高级的线性代数函数库已经能够利用多核CPU的多个核心来并行地处理矩阵运算,这也是算法的向量化实现如此重要的缘故(比调用循环快)。
5. iteration/batch-size/epoch
- iteration:表示1次迭代(也叫training step),每次迭代更新1次网络结构的参数;
- batch-size:1次迭代所使用的样本量;
- epoch:1个epoch表示过了1遍训练集中的所有样本。
值得注意的是,在深度学习领域中,常用带mini-batch的随机梯度下降算法(Stochastic Gradient Descent, SGD)训练深层结构,它有一个好处就是并不需要遍历全部的样本,当数据量非常大时十分有效。此时,可根据实际问题来定义epoch,例如定义10000次迭代为1个epoch,若每次迭代的batch-size设为256,那么1个epoch相当于过了2560000个训练样本。
batch_sizea大小对模型训练的影响
- batch size过小,花费时间多,同时梯度震荡严重,不利于收敛;batch size过大,不同batch的梯度方向没有任何变化,容易陷入局部极小值。
- 大batch是降低了梯度里的噪声,带来的影响就是sgd中随机的部分减弱了,具体表现为泛化变差和收敛变慢(同等epoch情况下),泛化差可以用增加训练epoch来弥补,但是这样就不符合分布式训练的初衷,所以一般采用的linear scale rule等效线性增加lr配合warmup来弥补收敛和泛化上的差距(之前也有人说是sqrt的,最近比较认可的是lr和batch是线性关系)