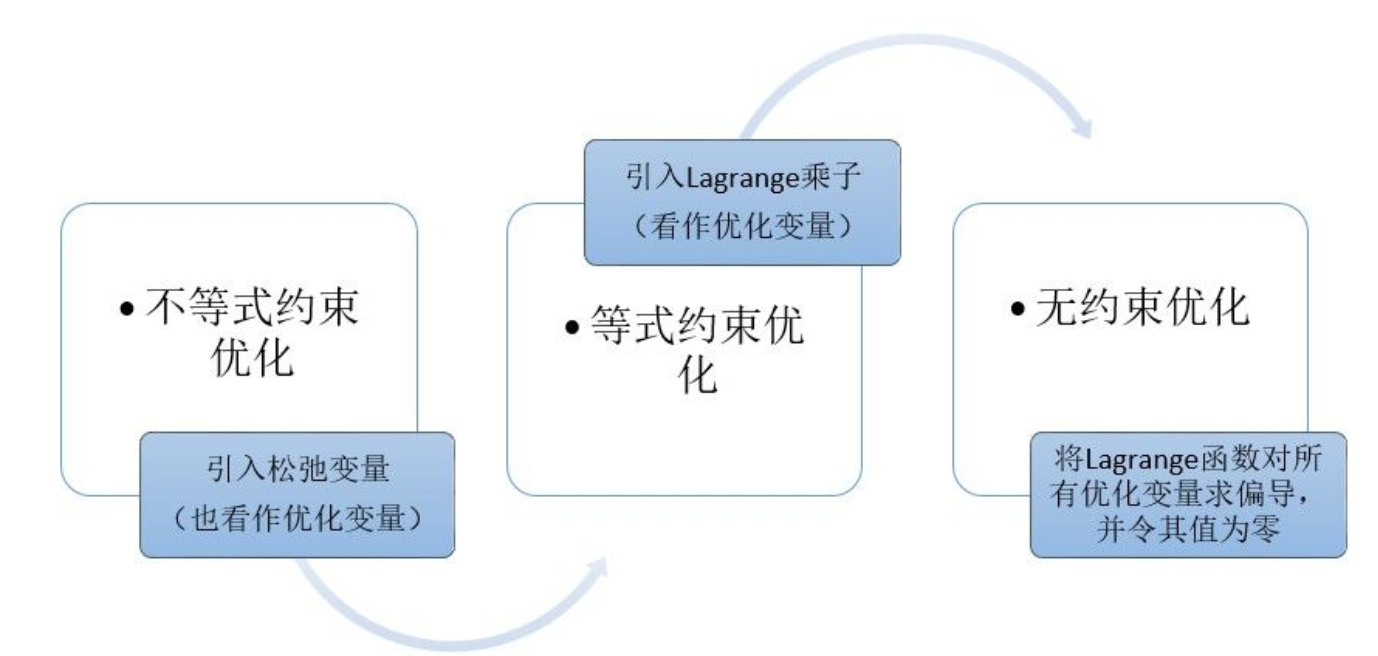
给定优化问题：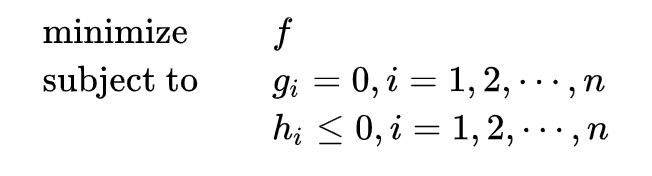
那么我们可以通过KKT条件求得该不等式优化问题的极值：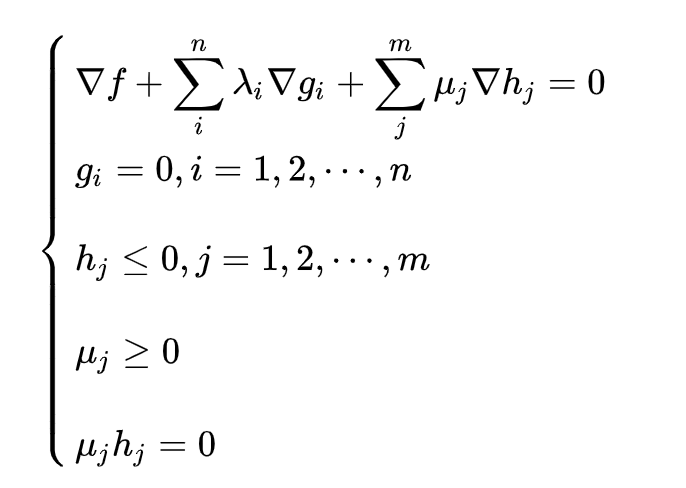
进一步解释一下KKT条件中的各个项的含义：
KKT条件是拉格朗日乘数法的推广，那么首先介绍一下拉格朗日乘数法
1. 拉格朗日乘数法
拉格朗日乘数法是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。
1.1 等式约束优化问题
1.2 不等式约束优化问题(KKT条件)
专业概念总结
要确保一下概念完全理解，你才能过关：
若有收获，就点个赞吧
0 人点赞
