1. 基础概念
正则化是为了防止模型过拟合、提高模型泛化能力的一种方法。
正则化后的目标函数变成了原始损失函数+额外项，常用的额外项一般有两种，英文称作ℓ1−𝑛𝑜𝑟𝑚和ℓ2−𝑛𝑜𝑟𝑚，中文称作L1正则化(Lasso回归)和L2正则化(Ridge岭回归)，或者L1范数和L2范数（实际是L2范数的平方）。
线性回归L1正则化损失函数：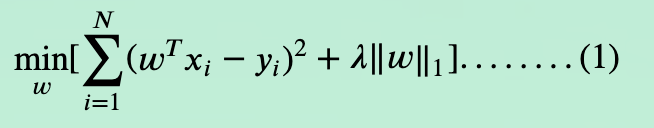
线性回归L2正则化损失函数：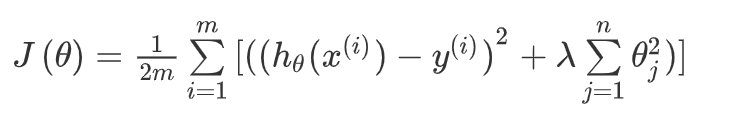
如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对进行正则化，所以梯度下降算法将分两种情形：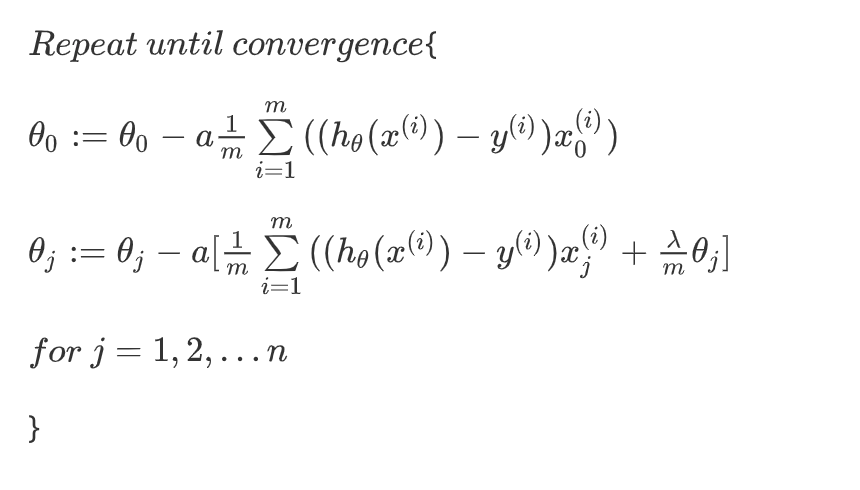
对上面的算法中
时的更新式子进行调整可得：
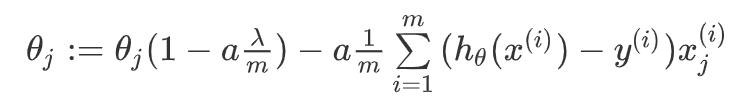
可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令
值减少了一个额外的值。
2. L1，L2正则化区别
- L1正则化是指权值向量𝑤中各个元素的绝对值之和，通常表示为‖𝑤‖1。
- L2正则化是指权值向量𝑤中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为‖𝑤‖22。
- L1正则化可以使得参数稀疏化，即得到的参数是一个稀疏矩阵，可以用于特征选择。
- L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合。
3. 原理解释
参考我的另一篇博文可知， “带正则项”和“带约束条件”是等价的。
为了约束w的可能取值空间从 而防止过拟合，我们为该最优化问题加上一个约束，就是w的L2范数的平方不能大于m：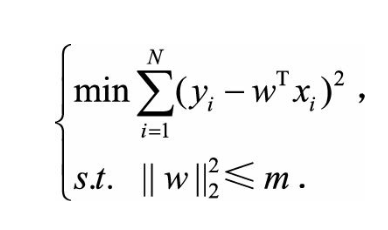
为了求解带约束条件的凸优化问题，根据拉格朗日乘数法可写出拉格朗日函数：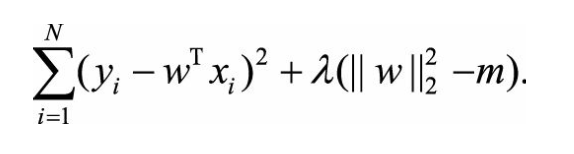
若w和λ分别是原问题和对偶问题的最优解，则根据KKT条件，它们应满足：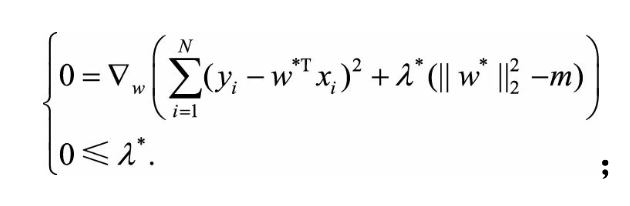
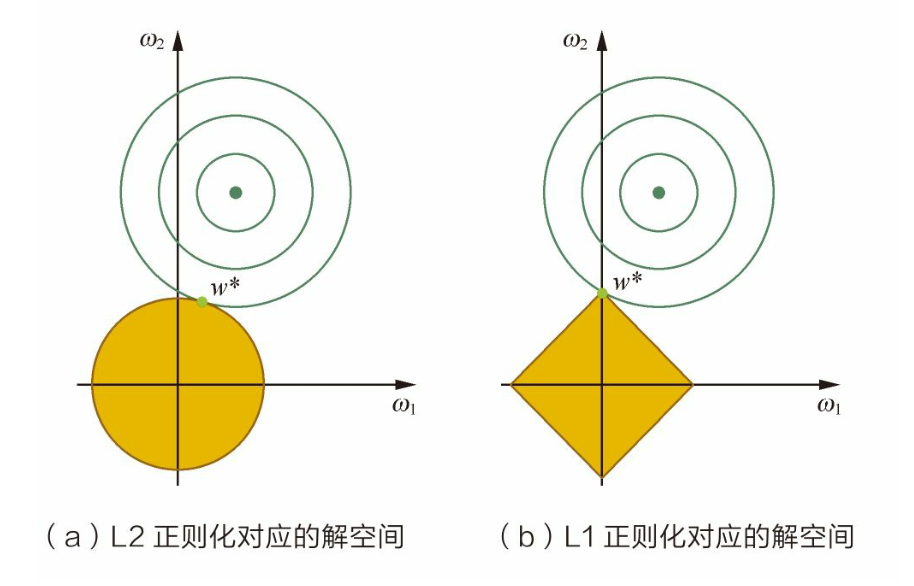
L2正则化相当于为参数定义了一个圆形 的解空间(因为必须保证L2范数不能大于m)，而L1正则化相当于为参数定义了 一个棱形的解空间。如果原问题目标函数的最优解不是恰好落在解空间内，那么约束条件下的最优解一定是在解空间的边界上，而L1“棱角分明”的解空间显然更 容易与目标函数等高线在角点碰撞，从而产生稀疏解。
参考文献
若有收获，就点个赞吧
0 人点赞
