1. LR
1.1 场景
逻辑回归（Logistic Regression）是机器学习中的一种分类模型，由于算法的简单和高效，在实际中应用非常广泛。先以二分类为例，训练形式数据如下：
为训练数据样本个数；
是一个m维向量，代表一个数据集样本有m个特征；
取值0或1，代表样本所属类别。
我们的问题可以简化为，如何找到这样一个决策函数
，它在
未知的数据集上能有足够好的表现(正确预测出
)。至于如何衡量一个二分类模型的好坏，我们可以用分类错误率这样的指标：
，也可以用准确率，召回率，AUC等指标来衡量。
值得一提的是，模型效果往往和所用特征密切相关。特征工程在任何一个实用的机器学习系统中都是必不可少的，具体的特征工程可参考我的另一篇博文。
1.2 sigmoid函数
sigmoid函数又叫Logistic函数，它在机器学习领域有极其重要的地位。
sigmoid函数公式：
函数图像：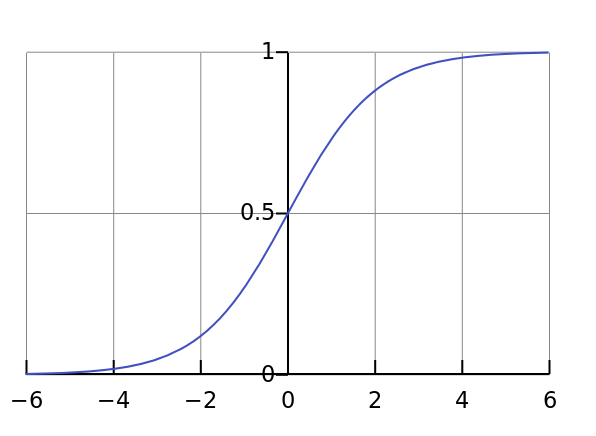
函数基本性质：
- 定义域
，值域
； - 在定义域内连续光滑递增；
- 在定义域内可导，且
最早Logistic函数是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。广义Logistic曲线可以模仿一些情况人口增长（P）的 S 形曲线。起初阶段大致是指数增长；然后随着开始变得饱和，增加变慢,最后，达到成熟时增加停止.
sigmoid函数在机器学习中最常用的就是LR模型中了。
1.3 为什么选择sigmoid函数？
基础不好的同学可以选择跳过这一小节。
sigmoid函数和跃阶函数比较像，但可导，所以其良好的性质适合LR任务。 可以参考这篇比较靠谱的答案。 大致意思是：
- 由于sigmoid函数有很好的性质，但这只能说明sigmoid函数可用，不是为什么要用它，因为其他函数比如tanh函数也具有相同的性质和效果。
- 这个其实才是为什么使用sigmoid函数的原因（数学背后原理证明）。LR前提是假设样本服从伯努利分布，数学证明伯努利分布的指数簇形式就是sigmoid函数的形式，而指数簇满足最大熵思想，也就是说对于经验分布利用最大熵原理导出的分布就是指数族分布。
1.3 LR决策函数
一个机器学习的模型，实际上是把决策函数限定在某一组条件下，这组限定条件就决定了模型的假设空间。当然，我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是：
这里的
就是上面提到的sigmoid函数，相应的决策函数为：
选择0.5作为阈值是一个一般的做法，实际应用时特定的情况可以选择不同阈值，如果对正例的判别准确性要求高，可以选择阈值大一些，对正例的召回要求高，则可以选择阈值小一些。
1.4 参数求解
模型的数学形式确定后，剩下就是如何去求解模型中的参数。统计学中常用的一种方法是最大似然估计，即找到一组参数，使得在这组参数下，我们的数据的似然度（概率）越大。在逻辑回归模型中，似然度可表示为：
取对数可以得到对数似然度：
另一方面，在机器学习领域，我们更经常遇到的是损失函数的概念，其衡量的是模型预测错误的程度。常用的损失函数有0-1损失，log损失，hinge损失等，关于损失函数种类的细节可以参考我的另一篇文章。其中log损失在单个数据点上的定义为
如果取整个数据集上的平均log损失，我们可以得到：
即在逻辑回归模型中，我们最大化似然函数和最小化log损失函数实际上是等价的。对于该优化问题，存在多种求解方法，具体优化算法可以参考我的另一篇博文，这里以梯度下降的为例说明，其中根据LR损失函数计算其梯度可得到：
沿梯度负方向选择一个较小的步长可以保证损失函数是减小的，另一方面，逻辑回归的损失函数是凸函数（加入正则项后是严格凸函数），可以保证我们找到的局部最优值同时是全局最优。此外，常用的凸优化的方法都可以用于求解该问题。例如共轭梯度下降，牛顿法，LBFGS等，这些高级优化算法是大型机器学习常用到的，具体细节可以参考我的另一篇文章。
1.5 分类边界
逻辑回归本质上是一个线性模型，但是，这不意味着只有线性可分的数据能通过LR求解，实际上，我们可以通过特征变换的方式把低维空间转换到高维空间，而在低维空间不可分的数据，到高维空间中线性可分的几率会高一些。下面两个图的对比说明了线性分类曲线和非线性分类曲线（通过特征映射）：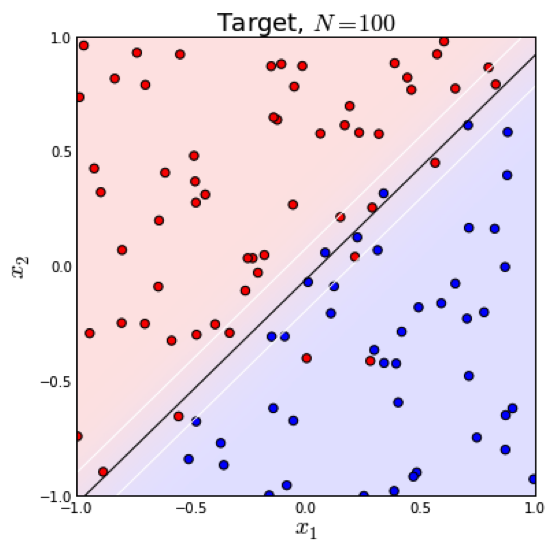
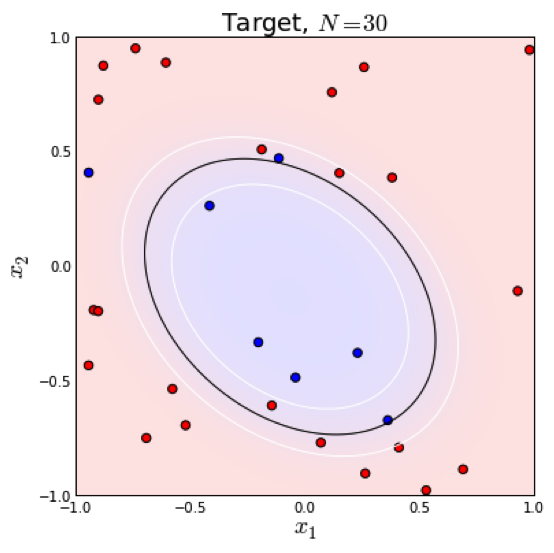
左图是一个线性可分的数据集，右图在原始空间中线性不可分，但是在特征转换
后的空间是线性可分的，对应的原始空间中分类边界为一条类椭圆曲线。
1.6 正则化
当模型的参数过多时，很容易遇到过拟合的问题。这时就需要有一种方法来控制模型的复杂度，典型的做法在优化目标中加入正则项，通过惩罚过大的参数来防止过拟合：
一般情况下，取p=1或p=2，分别对应L1，L2正则化，L1正则化（左图）倾向于使较多的参数变为0，因此能产生稀疏解，而L2正则化则将全部参数都趋近于0，但不等于0。
实际应用时，由于我们数据的维度可能非常高，L1正则化因为能产生稀疏解，使用的更为广泛一些。 关于L1，L2正则化的细节可以参考我的另一篇文章。
由于LR模型的简单高效，易于实现，可以为后续模型优化提供一个不错的baseline。
1.7 延伸
1.8 细节问题
LR分类模型为什么用交叉熵损失函数，而不用MSE?
首先说一下交叉熵，其实LR的损失函数
这一形式从信息论的角度来讲就是交叉熵的形式，具体有关各种熵的讲解可参考我的另一篇博文。
为什么不是用MSE即线性模型使用的均方误差损失函数而使用这种交叉熵的形式呢：
这里的本质原因还是线性模型和分类模型的假设函数不同造成的，分类模型就在线性模型的基础上外套了一层sigmoid函数(二分类)或者softmax函数(多分类)，这就导致了如果分类还是用MSE做损失函数的话，其函数图像并不是像线性模型那样的凸函数，而是如下所示：
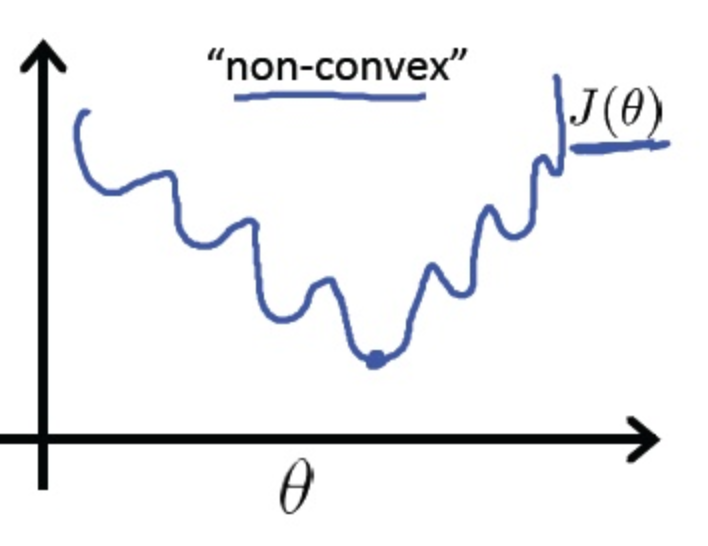而我们在利用梯度下降或者其他优化算法时，一旦函数非凸那么容易陷入局部最优，无法到达全局最优，用梯度下降求解时，凸优化问题有很好的收敛特性，所以我们应尽量使我们的损失函数为凸函数，使参数的优化问题化为凸优化问题，而交叉熵损失函数就能够达到这一目的。LR为什么用离散特征
在工业界，很少直接将连续值作为特征喂给逻辑回归模型，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：
- 异常值鲁棒性强，不容易过拟合。针对于年龄这个特征，如果不分段，出现300会对模型带来很大的扰动行，而如果离散化后，大于30的统一编码为1，从而减少异常值对模型的扰动，增强模型鲁棒性。
- 提升表达能力。一个特征离散化为多个特征后，原来的单特征对应单权重，而离散化后的每段分别对应一个权重，这种分段的能力为模型带来类似折线的非线性拟合能力。
LR为什么如何解决非线性题
- LR是广义的线性模型，但后面通过接入sigmoid函数引入非线性，所以是非线性模型。
- 进一步可以通过人工特征组合引入非线性能力。
为什么LR的参数可以初始化为0，而NN中不能
由实际的参数更新公式就可以看出，LR的参数更新公式如下：
可看出，参数w在更新时，会随着x的不同而不同，所以w初始化为0或者任何形式都可以。而神经网络的参数的更新公式如下：
可看出，神经网络中参数的更新依然该参数前一次的数值，若初始化为0则参数会一直为0，不进行更新（当然最后一层除外）。
其实，NN中的最后一层的一个节点就相当于LR的变体，区别就是NN是多层互相关联的，LR只是NN中的最后一层的一个节点而已。
2. 从LR到FM和FFM
FM英文全称是“Factorization Machine”，简称FM模型，中文名“因子分解机”，2010年由Rendle提出。
2.1 从LR到SVM再到FM模型
LR模型具有简单方便易解释容易上规模等诸多好处，但是，LR模型最大的缺陷就是人工特征工程，耗时费力费人力资源，那么能否将特征组合的能力体现在模型层面呢？
在计算公式里加入二阶特征组合即可，任意两个特征进行组合，可以将这个组合出的特征看作一个新特征，融入线性模型中。而组合特征的权重可以用来表示，和一阶特征权重一样，这个组合特征权重在训练阶段学习获得。其实这种二阶特征组合的使用方式，和多项式核SVM是等价的。虽然这个模型看上去貌似解决了二阶特征组合问题了，但是它有个潜在的问题：它对组合特征建模，泛化能力比较弱(具体为什么看下一段落)，尤其是在大规模稀疏特征存在的场景下，这个毛病尤其突出，比如CTR预估和推荐排序，这些场景的最大特点就是特征的大规模稀疏。所以上述模型并未在工业界广泛采用。那么，有什么办法能够解决这个问题吗？
于是，FM模型此刻可以闪亮登场了。如上图所示，FM模型也直接引入任意两个特征的二阶特征组合，和SVM模型最大的不同，在于特征组合权重的计算方法。FM对于每个特征，学习一个大小为k的一维向量，于是，两个特征
和
的特征组合的权重值，通过特征对应的向量
和
的内积
来表示。这本质上是在对特征进行embedding化表征，和目前非常常见的各种实体embedding本质思想是一脉相承的，但是很明显在FM这么做的年代（2010年），还没有现在能看到的各种眼花缭乱的embedding的形式与概念。所以FM作为特征embedding，可以看作当前深度学习里各种embedding方法的老前辈。
那么为什么说FM的这种特征embedding模式，在大规模稀疏特征应用环境下比较好用？为什么说它的泛化能力强呢？参考上图说明。即使在训练数据里两个特征并未同时在训练实例里见到过，意味着
一起出现的次数为0，如果换做SVM的模式，是无法学会这个特征组合的权重的。但是因为FM是学习单个特征的embedding，并不依赖某个特定的特征组合是否出现过，所以只要特征
和其它任意特征组合出现过，那么就可以学习自己对应的embedding向量。于是，尽管
这个特征组合没有看到过，但是在预测的时候，如果看到这个新的特征组合，因为
和
都能学会自己对应的embedding，所以可以通过内积算出这个新特征组合的权重。这是为何说FM模型泛化能力强的根本原因。
其实本质上，这也是目前很多花样的embedding的最核心特点，就是从0/1这种二值硬核匹配，切换为向量软匹配，使得原先匹配不上的，现在能在一定程度上算密切程度了，具备很好的泛化性能。
2.2 从MF到FM模型
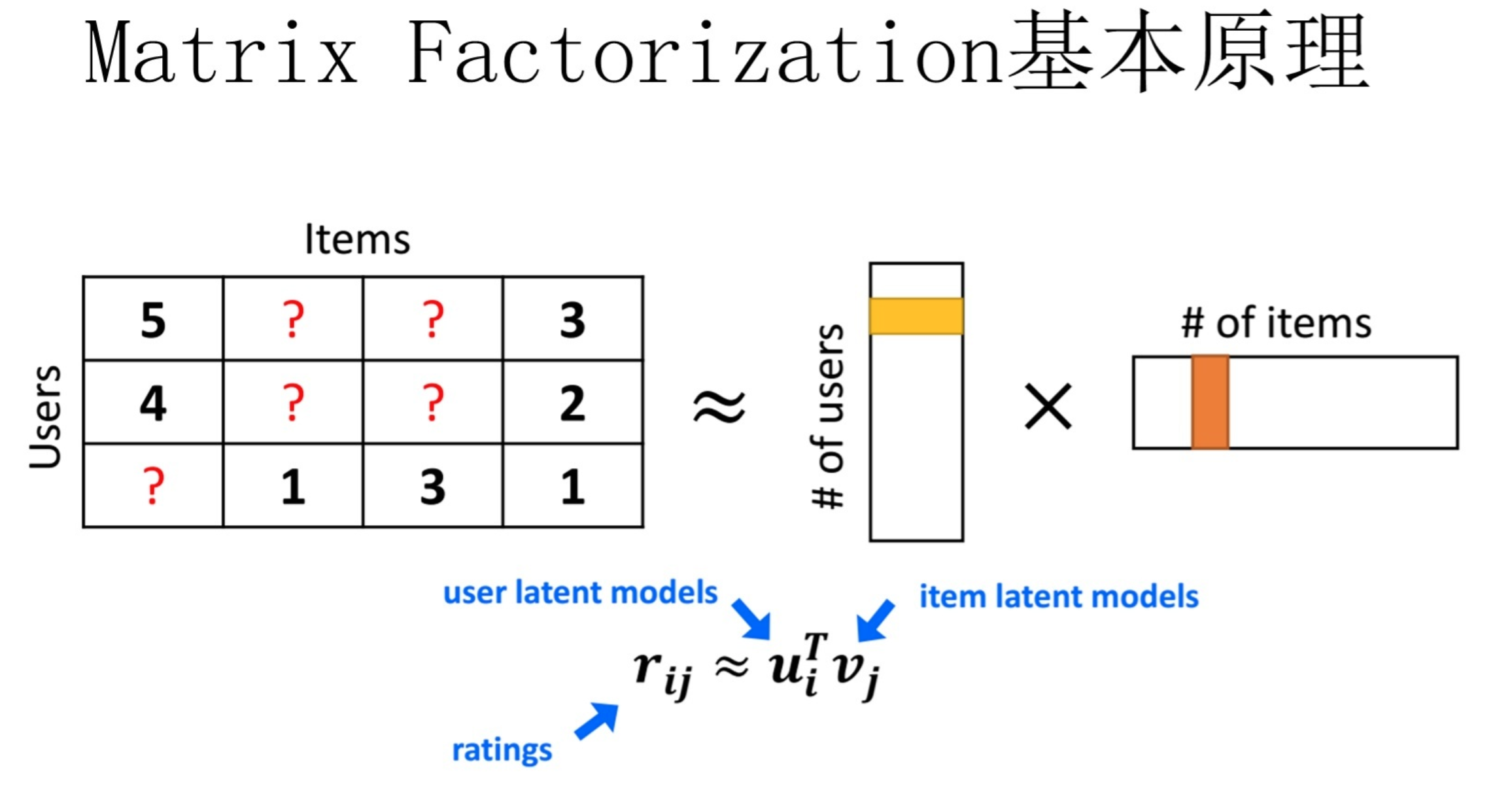
MF（Matrix Factorization，矩阵分解）模型是个在推荐系统领域里资格很深的老前辈协同过滤模型了。核心思想是通过两个低维小矩阵（一个代表用户embedding矩阵，一个代表物品embedding矩阵）的乘积计算，来模拟真实用户点击或评分产生的大的协同信息稀疏矩阵，本质上是编码了用户和物品协同信息的降维模型。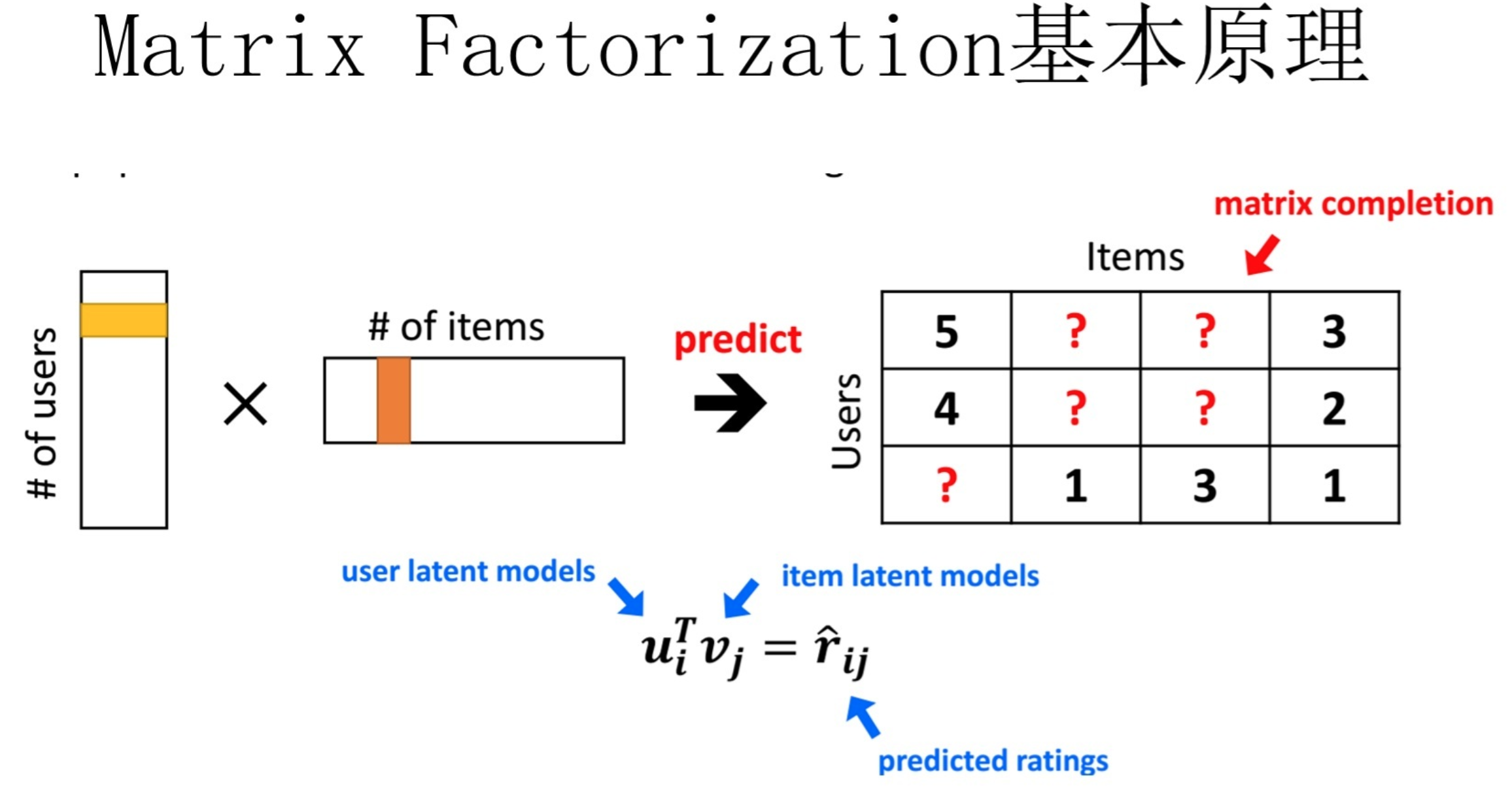
MF和FM不仅在名字简称上看着有点像，其实他们本质思想上也有很多相同点。本质上，MF模型是FM模型的特例，MF可以被认为是只有User ID 和Item ID这两个特征Fields的FM模型，MF将这两类特征通过矩阵分解，来达到将这两类特征embedding化表达的目的。而FM则可以看作是MF模型的进一步拓展，除了User ID和Item ID这两类特征外，很多其它类型的特征，都可以进一步融入FM模型里，它将所有这些特征转化为embedding低维向量表达，并计算任意两个特征embedding的内积，就是特征组合的权重。
2.3 FM算法时间复杂度
FM如今被广泛采用并成功替代LR模型的一个关键所在是：它可以通过数学公式改写，把表面貌似是
的复杂度降低到
，其中n是特征数量，k是特征的embedding size，这样就将FM模型改成了和LR类似和特征数量n成线性规模的时间复杂度了。
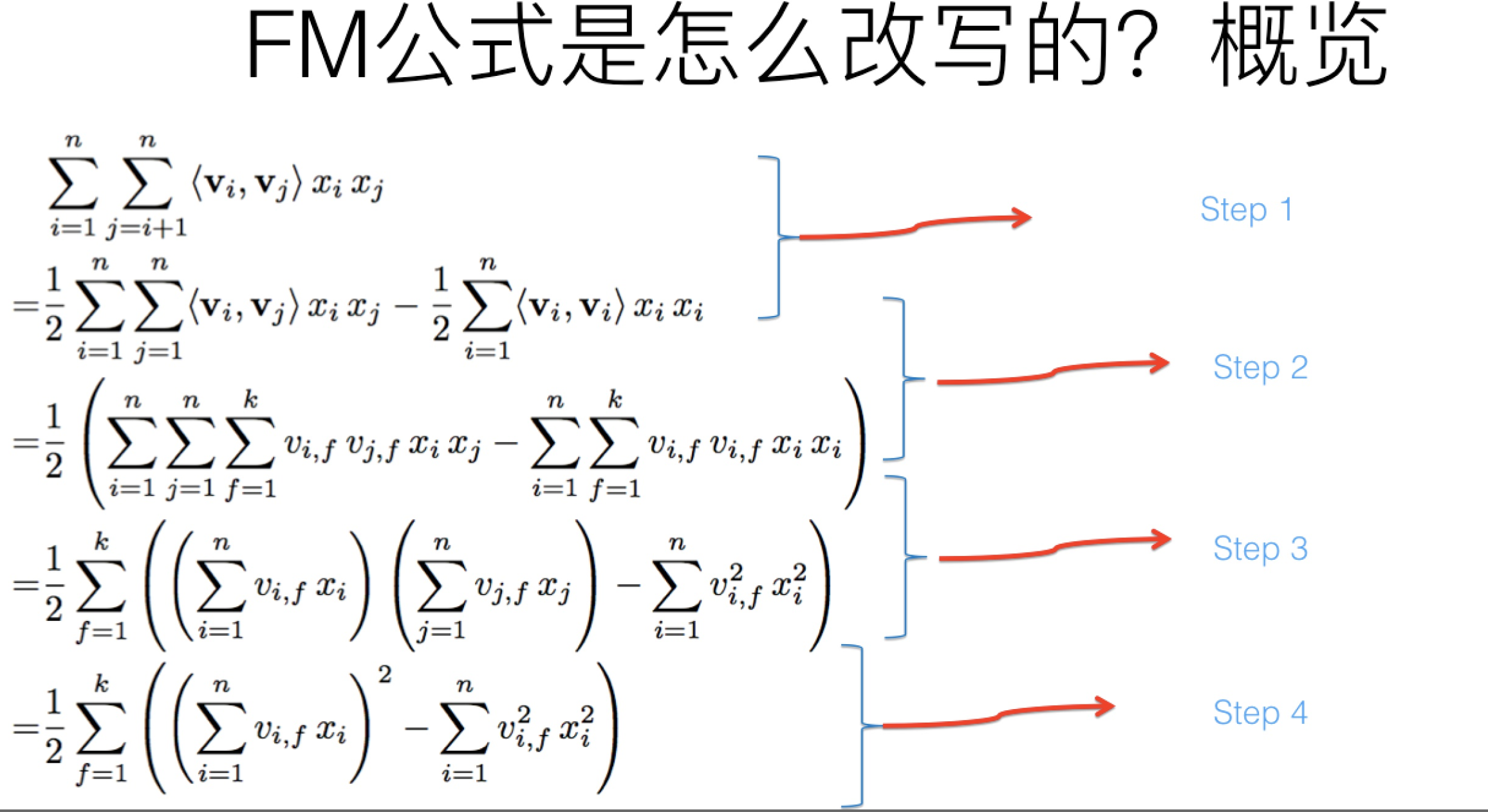
这里展开说一下step3，其他步都好理解：
其实吧，如果把k维特征向量内积求和公式抽到最外边后，公式就转成了上图这个公式了（不考虑最外边k维求和过程的情况下）。它有两层循环，内循环其实就是指定某个特征的第f位（这个f是由最外层那个k指定的）后，和其它任意特征对应向量的第f位值相乘求和；而外循环则是遍历每个的第f位做循环求和。这样就完成了指定某个特征位f后的特征组合计算过程。最外层的k维循环则依此轮循第f位，于是就算完了步骤三的特征组合。
对上一页公式图片展示过程用公式方式，再一次改写（参考上图），其实就是两次提取公共因子而已。虽说看上去n还有点大，但是其实真实的推荐数据的特征值是极为稀疏的，就是说大量xi其实取值是0，意味着真正需要计算的特征数n是远远小于总特征数目n的，无疑这会进一步极大加快FM的运算效率。
FFM在FM的基础上引入的field领域的概念，FM在每个特征embedding向量与其他特征做内积时用的是同一个向量，即共享向量
3. 从LR到NN(神经网络)
其实NN和LR有着千丝万缕的联系，具体细节可以参考我的另一篇博文。
4.wide&Deep
wide&deep实际上就是将LR与DNN模型融合在一下。
Wide侧记住的是历史数据中那些常见、高频的模式，是推荐系统中的“红海”，实际上，Wide侧没有发现新的模式，只是学习到这些模式之间的权重，做一些模式的筛选。正因为Wide侧不能发现新模式，因此我们需要根据人工经验、业务背景，将我们认为有价值的、显而易见的特征及特征组合，喂入Wide侧。
而Deep侧，通过embedding+深层交互，通过embedding将tag向量化，变tag的精确匹配，为tag向量的模糊查找，使自己具备了良好的“扩展”能力。
5. DeepFM与DeepFFM
DeepFM其实就是将wide&deep模型中的wide侧由LR替换为FM，从而在Wide侧能够自动学习二阶交叉特征。
参考文献
若有收获，就点个赞吧
0 人点赞
