review 统计概率：丰富多彩的概率分布

0. 先验/后验/似然的基本概念

1. 概率分布到底是啥，有啥用？

2. 几个重要概念的科普

2.0 离散变量和连续变量

• 如果随机变量的值可以都可以逐个列举出来，则为离散型随机变量，比如抛硬币。

• 如果随机变量X的取值无法逐个列举则为连续型变量，比如时间。

  2.1 概率分布函数和概率密度函数

  如果微积分是研究变量的数学，那么概率论与数理统计是研究随机变量的数学。 研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何。

• 概率密度函数只是针对连续性变量而言，而概率分布函数是对所有随机变量取值的概率的讨论，包括连续性和离散型。

• 从数学上看，分布函数F(x)=P(X

  2.2 期望

1. 定义

   设P(x)是一个离散概率分布函数，自变量的取值范围为{x1,x2,⋯,xn}。其期望被定义为： 设p(x)是一个连续概率密度函数。其期望为：

2. 性质

   设C为一个常数，X和Y是两个随机变量。以下是数学期望的重要性质：

   1. ，即一个常数的均值仍是他本身
   2. 
   3. 
   4. 当X和Y相互独立时，

3. 统计学意义

   即自变量取值的均值。

2.3 方差

1. 定义

   方差是一种特殊的期望，被定义为： 反复利用期望的线性性质，可以算出方差的另一种表示形式：

2. 性质

   1. 设C是常数，则，即常用无波动。
   2. 设X是随机变量，C是常数，则有，
   3. 设 X 与 Y 是两个随机变量，则，其中，即协方差，咱们再下一小节讨论。
   4. 如果两个变量X和Y相互独立，则

3. 统计学意义

   方差和标准差是测算离散趋势最重要、最常用的指标。方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程度的最重要的方法。标准差为方差的算术平方根，用S表示。标准差与方差不同的是，标准差和变量的计算单位相同，比方差清楚，因此很多时候我们分析的时候更多的使用的是标准差。

2.4 协方差

1. 定义

   两个随机变量的协方差被定义为： 进一步利用期望的性质：

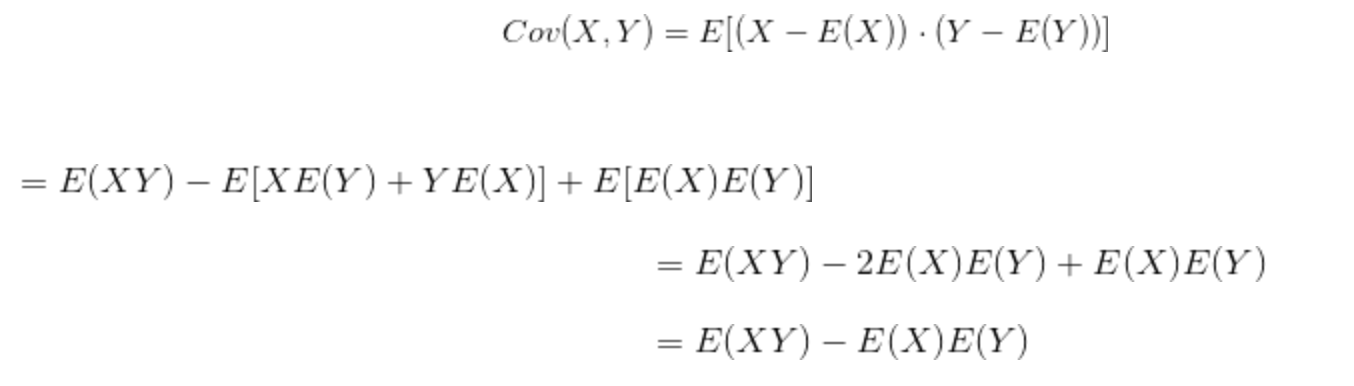
   因此方差是一种特殊的协方差。当x=y时，

2. 性质

   

3. 统计学意义

   从直观上来看，协方差表示的是两个变量总体误差的期望。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。 如果X与Y是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足E[XY]=E[X]E[Y]。 但是，反过来并不成立。即如果X与Y的协方差为0，二者并不一定是统计独立的。

2.5 相关系数

3. 几种常见的概率分布

3.0 伯努利分布

1. 定义：

   伯努利分布又称为两点分布或0-1分布。如果随机变量X只取0和1两个值，并且相应的概率为，则称随机变量X服从参数为p的伯努利分布。

2. 概率函数

   ,

3. 性质：

   ，

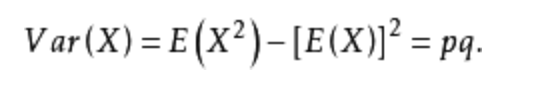
3.1 二项分布

1. 定义

   二项分布是由伯努利提出的概念，指的是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

2. 概率函数

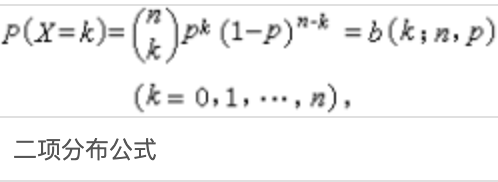
1. 性质

3.2 泊松分布(poisson)

1. 定义

   泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。

2. 概率函数

1. 性质

更形象化的解释可以参考这篇文章

3.3 几何分布

1. 定义

   几何分布（Geometric distribution）是离散型概率分布。其中一种定义为：在n次伯努利试验中，试验k次才得到第一次成功的机率。详细地说，是：前k-1次皆失败，第k次成功的概率。

2. 概率函数

1. 性质

   3.4 正态分布

2. 定义

   

3. 概率函数

4. 性质