0. 基础前提
1. 曼哈顿距离
为投影到各个维度上的距离和，二维表示即为两点的直角边距离和(如下图中红色表示)：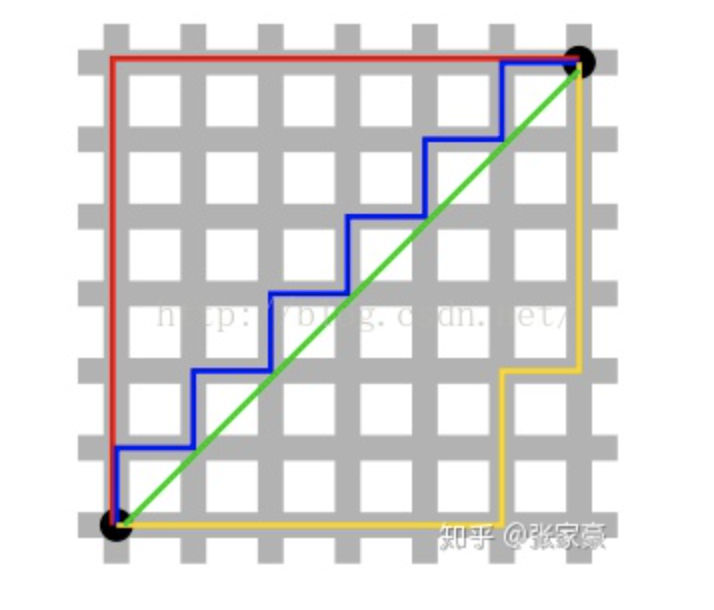
2. 欧式距离
两点之间的真实距离，二维表示即为两点的直线距离(如上图中的绿色表示)
4. 余弦距离
余弦相似度：两个向量间的夹角的余弦值，取值范围为[-1, 1]
余弦距离则为1-余弦相似度，取值范围[0,2]
余弦距离和欧式距离的转换：
在将向量x和y归一化后
此时余弦相似度为为
，余弦距离为
欧式距离为
可以看出在向量归一化后，欧式距离和余弦距离几乎等价
5. 马氏距离
马氏距离(Mahalanobis Distance)可以看作是欧氏距离的一种修正，修正了欧式距离中各个维度尺度不一致且相关的问题。它可以表示点与一个分布之间的距离。
6. 杂
严格定义的距离
需要满足三个特性：正定性，对称性，三角不等式
正定性：
对称性：
三角不等式：
余弦相似度就不是严格定义的距离，因为不满足三角不等式，比如
欧氏距离和余弦距离的应用场景
总体来说，欧氏距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异。
例如，统计两部剧的用户观看行为，用户A的观看向量为(0,1)，用户B为 (1,0)；此时二者的余弦距离很大，而欧氏距离很小；我们分析两个用户对于不同 视频的偏好，更关注相对差异，显然应当使用余弦距离。而当我们分析用户活跃 度，以登陆次数(单位：次)和平均观看时长(单位：分钟)作为特征时，余弦距离会 认为(1,10)、(10,100)两个用户距离很近；但显然这两个用户活跃度是有着极大差异 的，此时我们更关注数值绝对差异，应当使用欧氏距离。
正定性，
这对称性，三角不等式
若有收获，就点个赞吧
0 人点赞
