1. 统计整体信息
df.head()df.describe()df.info()df['A'].value_counts()
2. 缺失值填充
| 缺失比例 | 缺失比例过高 | 缺失比例适中 | 缺失比例较少 | |
|---|---|---|---|---|
| 特征类型 | 离散特征 | 连续特征 | ||
| 处理方法 | 可以舍弃该特征 |
可选择把NaN作为一个新类别,加到特征中去 |
可选择给定一个步长离散化后,将NaN作为一个type加入到属性类目中 | 可选择根据已有数据拟合填充 (默认/固定值、均值、中位数、众数、插值法、KNN填充、把缺失值作为label预测填充等) |
| 代码示例 | df.drop([‘a’, ‘b’]) | df.loc[df.fea.isnull(), ’fea’] = ‘Yes’ df.loc[df.fea.notnull(), ’fea’] = ‘No’ |
pd.fillna(0, inplace=True) pd.fillna(pd.mean(),inplace=True) pd.fillna(pd.mean(),inplace=True) pd.fillna(pd.median(),inplace=True) pd.fillna(pd.mode(),inplace=True) |
3. 异常值处理
3.1 异常值检测
3.1.1 3∂原则
如果数据服从正态分布,在3∂原则下,异常值为一组测定值中与平均值的偏差超过3倍标准差的值。如果数据服从正态分布,距离平均值3∂之外的值出现的概率为P(|x-u| > 3∂) <= 0.003,属于极个别的小概率事件。如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。
3.1.2 箱型图分析
利用数据中的五个统计量:最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法,它也可以粗略地看出数据是否具有有对称性,分布的分散程度等信息。
第一四分位数(Q1):表示全部观察值中有四分之一的数据取值比它小. 第三四分位数(Q3),表示全部观察值中有四分之一的数据取值比它大;
IQR为四分位数间距,是上四分位数QU与下四分位数QL的差值,包含了全部观察值的一半。
如下图(来自百度经验)所示,如果值小于Q1-1.5IQR, 或者大于Q3 + 1.5IQR,认为数据为异常值。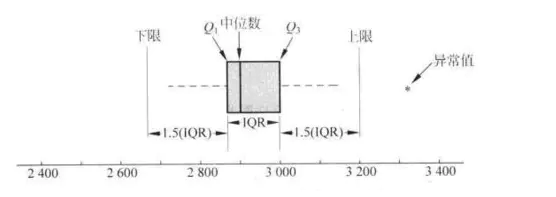
3.1.3 Z-score
Z-score又称为标准分数(Standard Score), 可用来帮助识别异常值。Z-score的值求取如下: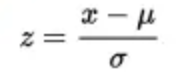
建议将Z分数低于-3或高于3的数据看成是异常值。这些数据的准确性要复查,以决定它是否属于该数据集。计算Z值时需要“母体”的平均值和标准差,而不是“样本”的平均值和标准差。因此需要了解母体的统计数据资料。但是要确实了解母体真正的标准差往往是不切实际的。
3.1.4 基于距离
利用聚类的思想,对数据进行聚类,排除距离中心最远的n个点,一般算法:kmeans,knn等
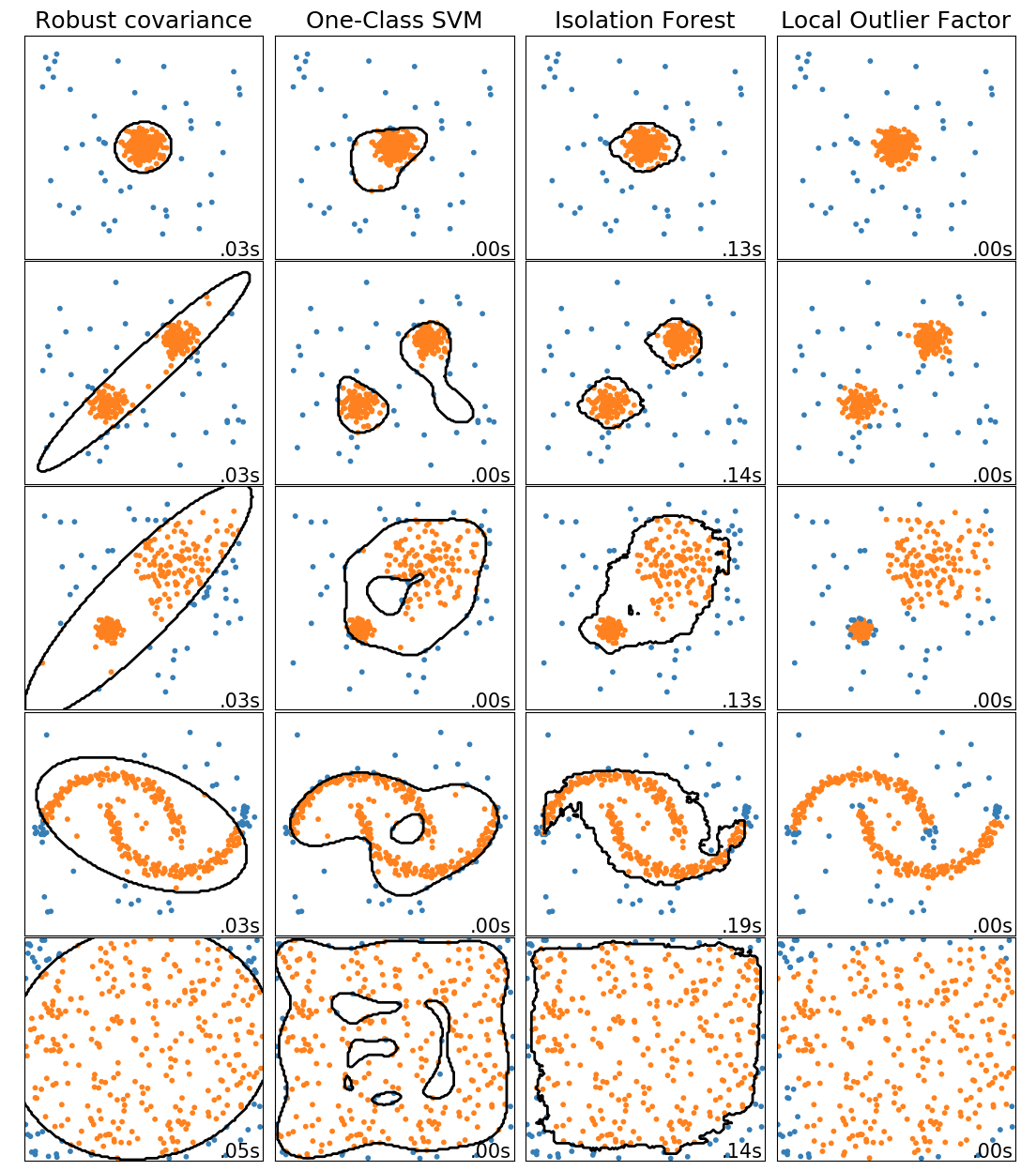
sklearn中用到了LOF(LocalOutlierFactor),即局部离群因子;Isolation Forest(孤立森林)等方法。各种算法效果如下:
3.2 异常值处理
离群值的处理和缺失值方式类似,可以把离群值当成缺失值处理。
1.删除 2.中位值或者均值 3.差值法 4.相似样本
4. 特征编码 (离散化)
我们在使用LR、FM等模型时,往往偏向于将许多特征离散化处理,那么为什么要离散化,有什么意义和益处呢?
离散化后的特征对异常数据有很强的鲁棒性,模型会更稳定;
比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰; 比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问,很多时候涉及到业务知识层面的东西;
特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险;
连续特征实际上意味着更多的离散值。分箱进一步降低了变量取值的数量,起到了简化模型的作用。 当使用连续特征时,一个特征对应于一个权重,那么,如果这个特征权重较大,模型就会很依赖于这个特征,这个特征的一个微小变化可能会导致最终结果产生很大的变化,这样子的模型很危险,当遇到新样本的时候很可能因为对这个特征过分敏感而得到错误的分类结果,也就是泛化能力差,容易过拟合。而使用离散特征的时候,一个特征变成了多个,权重也变为多个,那么之前连续特征对模型的影响力就被分散弱化了,从而降低了过拟合的风险。
离散化后通过one-hot可以引入非线性。此外可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
离散化在onehot展开之后还可以进行特征交叉(与FM模型类似),这一系列增大特征维度的方法都可以增强逻辑回归这种线性模型的非线性表达能力,根据计算学习理论的covar定理可得,一般来说特征维度越高则线性可分或线性可拟合的概率越高,当然过拟合的概率也越大。 下面从直观角度给出解释: 我们假设决策面为y=x^2,且模型是只具有一维特征x的线性模型,即模型的表达形式为:y=kx+b,如下图所示:
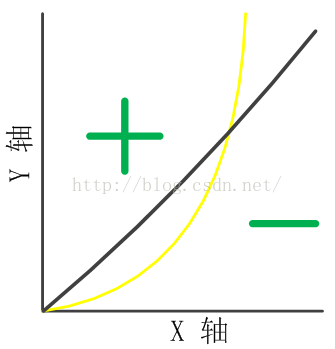 显然,模型不能很好地拟合决策面,那么,假如将x离散化成多个0/1特征(one-hot编码):
显然,模型不能很好地拟合决策面,那么,假如将x离散化成多个0/1特征(one-hot编码):

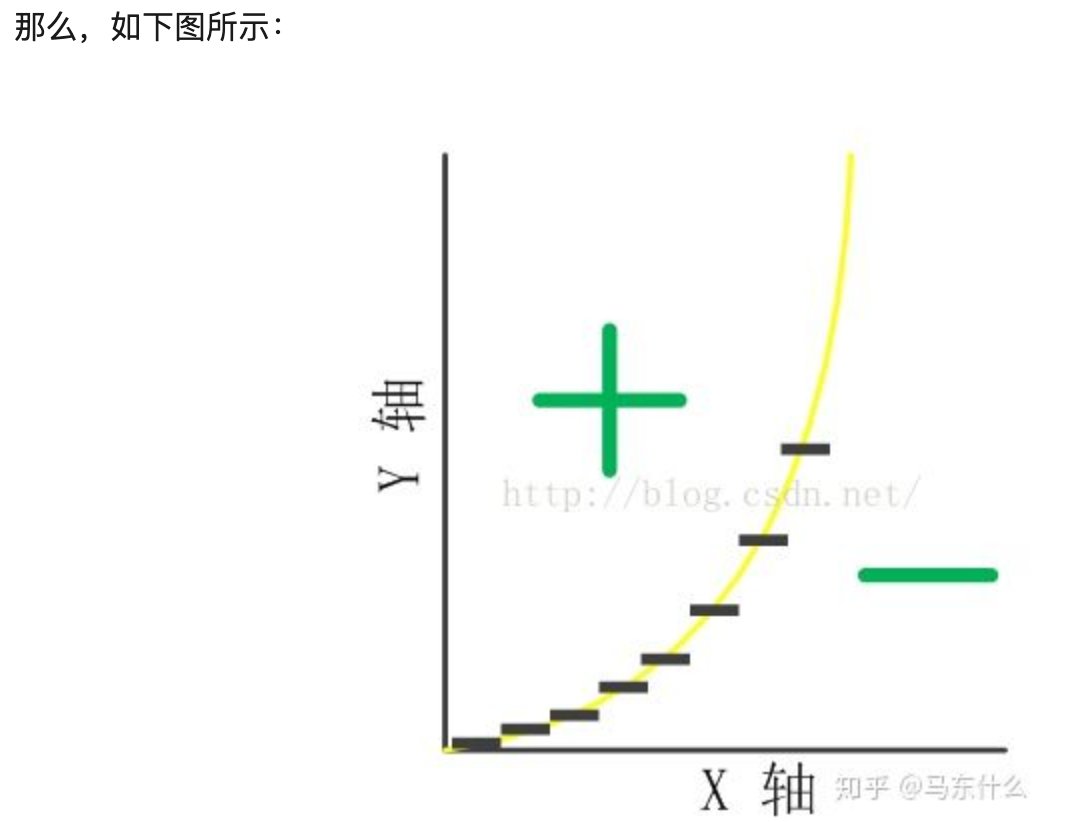 这也能够直观显示出离散化进一步引入非线性的能力。
这也能够直观显示出离散化进一步引入非线性的能力。离散特征的增加和减少都很容易,易于模型的快速迭代;(???)
比如说我们当前训练集的年龄是20~30岁,假设在20~30之间分了5个箱子离散化然后onehot展开,下一次训练的时候如果出现超过30岁的特征,那么直接增加一列0-1特征用来表示用户是否超过30岁即可; (离散特征的增加和减少,模型也不需要调整,重新训练是必须的,相比贝叶斯推断方法或者树模型方法迭代快)
稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
稀疏矩阵可以使用稀疏矩阵的存储方式,比如python中的csr_matrix模块,通过稀疏矩阵的存储方式对原始数据进行了压缩。
总之用李沐大神的一句话概括一下:
模型是使用离散特征还是连续特征,其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型,也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说,前者容易,而且可以n个人一起并行做,有成功经验;后者目前看很赞,能走多远还须拭目以待。
具体的离散化方法又是另一很大的领域问题,常用到的方法有等频分箱、等宽分箱和优化分箱。
最优离散化问题已经被证明是一个NP-hard问题
等宽分箱:将连续型变量的取值范围均匀划成n等份,每份的间距相等。
等频分箱:它把观察点均匀分为n等份,每份内包含的观察点数相同。
等频分箱将原有变量的分布转变成了均匀分布。而等宽分箱可以保持数据原有的分布,分箱数越多对数据原貌保持得越好。
优化分箱:我们需要引入一个评价标准来判断什么样的宽度是合适的,什么样频率是合适的。评价标准可以是IV值,熵或者互信息系数,它衡量了该变量与目标变量之间的相关关系。如果我们选择了IV值作为评价标准,那么在多次划分中,都要计算分箱后的变量与目标变量之间的IV值,最后选择IV值最大的划分作为最优的划分方式。
sklearn中常用到
preprocessing.KBinsDiscretizer模块进行离散化处理,其中strategy的参数取uniform时为等宽分箱,quantile为等频分箱,kmeans为聚类分箱。
5. 特征归一/标准化 (连续化)
这里说明一点,大家不要纠结于归一化和标准化到底啥区别,其实二者都属于对特征数值进行缩放的方法。
第一种对应sklearn中的
preprocessing.MinMaxScaler()模块; 第一种对应sklearn中的preprocessing.StandardScaler()模块;