review 最优化算法: 从GD(梯度下降)到Adam

0. 数学基础

0.1 导数

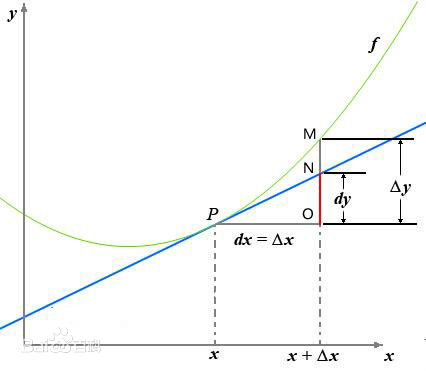
定义：
反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。

0.2 偏导数

定义：一个多变量的函数的偏导数(partial derivative)是它关于其中一个变量的导数。
可以看到，导数与偏导数本质是一致的，都是当自变量的变化量趋于0时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。区别在于：

导数，指的是一元函数中，函数在某一点处沿x轴正方向的变化率； 偏导数指的是多元函数中，函数在某一点处沿某一坐标轴（x1,x2,…,xn）正方向的变化率。

0.3 方向导数

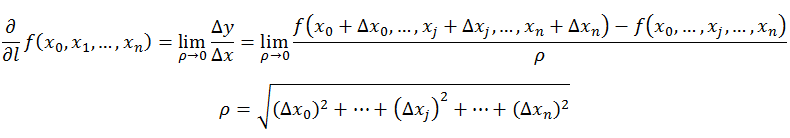
定义：在函数定义域的内点，对某一方向求导得到的导数。
在前面导数和偏导数的定义中，均是沿坐标轴正方向讨论函数的变化率。那么当我们讨论函数沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一趋近方向上的导数值。
　通俗的解释是，我们不仅要知道函数在坐标轴正方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。

0.4 梯度

定义：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

1. GD梯度下降family

梯度下降优化法经历了 SGD→SGDM→NAG→AdaGrad→AdaDelta→Adam→Nadam 这样的发展历程。之所以会不断地提出更加优化的方法，究其原因，是引入了动量（Momentum）这个概念。最初，人们引入一阶动量来给梯度下降法加入惯性（即，越陡的坡可以允许跑得更快些）。后来，在引入二阶动量之后，才真正意味着“自适应学习率”优化算法时代的到来。
其实，所有梯度下降法都遵循一个基本框架通式，掌握这个通式，其他的就容易多了。首先给出一些基本符号的定义：

• 待优化参数：
• 目标函数：
• 学习率：

下面开始介绍通用框架：
对于每个epoch t，进行如下迭代：

1. 计算目标函数关于当前参数的梯度：
2. 根据历史梯度计算一阶和二阶动量(之后会详细讲述如何计算)：

1. 更新参数：，其中为平滑项，防止分母为零，通常取 1e-8。

以下所有算法全部是基于这个通用框架的。

2. SGD

SGD (Stochastic Gradient Descent) ，即随机梯度下降，最为简单，它没有动量的概念，或者可以说是，(单位矩阵，相当于一维运算中的1)，。所以SGD的参数更新公式为：

SGD的缺点是收敛过慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点。

3. SGDM

为了抑制 SGD 的震荡，SGDM(Momentum)引入了惯性，即一阶动量。如果发现是陡坡，就用惯性跑得快一些。此时，，二阶动量依旧未引入，即，。我们把这个式子递归一下就可以看出，一阶动量其实是各个时刻梯度方向的指数移动平均值，约等于最近个时刻的梯度向量和的平均值。所以SGDM的参数更新公式为：

的经验值为 0.9 ，也就是每次下降时更偏向于此前累积的下降方向，并稍微偏向于当前下降方向，这使得参数中那些梯度方向变化不大的维度可以加速更新，并减少梯度方向变化较大的维度上的更新幅度。由此产生了加速收敛和减小震荡的效果。

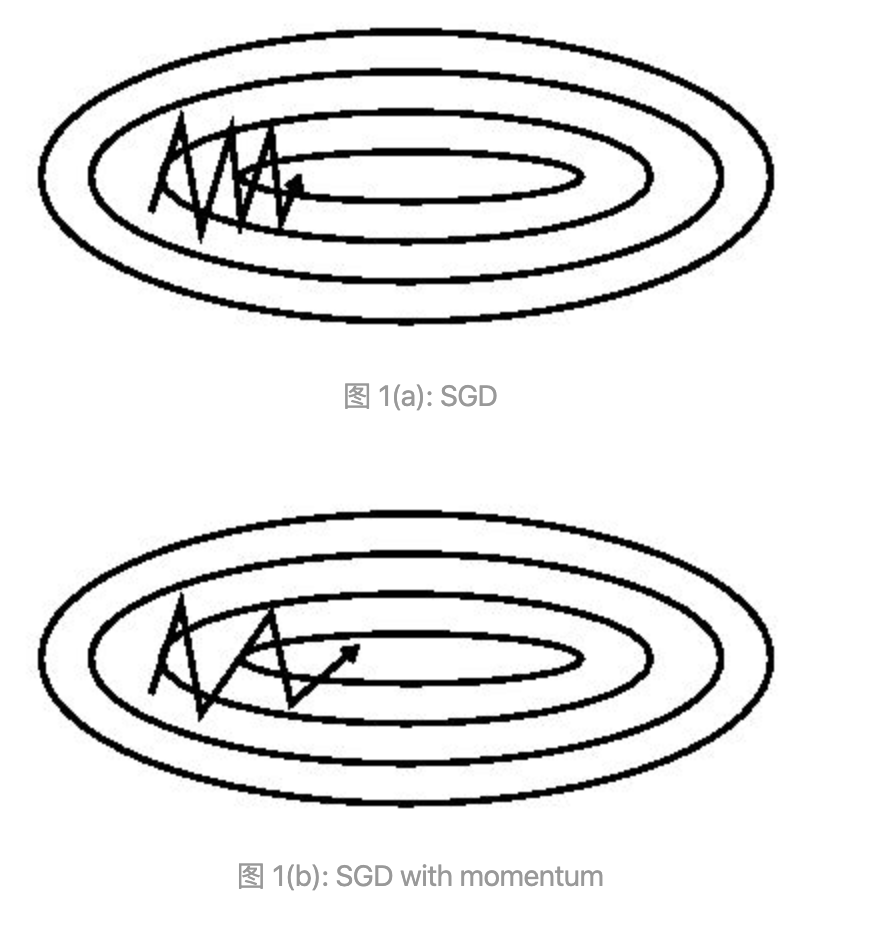
可以看出，SGDM加速了梯度下降收敛过程

4. NAG

在SGDM基础上，Nesterov Accelerated Gradient提出了一个方法是既然我们有了动量，那么我们可以在步骤 1 中先不考虑当前的梯度。每次决定下降方向的时候先按照一阶动量的方向走一步试试，然后在考虑这个新地方的梯度方向。此时的梯度就变成了：。我们用这个梯度带入 SGDM 中计算 mt 的式子里去，然后再计算当前时刻应有的梯度并更新这一次的参数。所以NAG的参数更新公式为：

5. AdaGrad

到这里，终于引入了二阶动量，涉及到了自适应学习率的优化算法。SGD、SGDM 和 NAG 均是以相同的学习率去更新的各个分量。而深度学习模型中往往涉及大量的参数，不同参数的更新频率往往有所区别。对于更新不频繁的参数（典型例子：更新 word embedding 中的低频词），我们希望单次步长更大，多学习一些知识；对于更新频繁的参数，我们则希望步长较小，使得学习到的参数更稳定，不至于被单个样本影响太多。
那么怎么样去度量历史更新频率呢？采用二阶动量——该维度上，所有梯度值的平方和：，我们发现引入二阶动量的意义实际是给了学习率一个缩放比例，从而达到了自适应学习率的效果（Ada = Adaptive）。（一般为了防止分母为 0 ，会对二阶动量做一个平滑。），对于此前频繁更新过的参数，其二阶动量的对应分量较大，学习率就较小，这一方法在稀疏数据的场景下表现很好。所以，AdaGrad的参数更新公式为：

但其仍存在一个问题，因为二阶动量是单调递增的，所以学习率会很快减至 0 ，这样可能会使训练过程提前结束。

6. AdaDelta/RMSProp

由于 AdaGrad 的学习率单调递减太快，我们考虑改变二阶动量的计算策略：不累计全部梯度，只关注过去某一窗口内的梯度。这个就是名字里 Delta 的来历。修改的思路很直接，前面我们说过，指数移动平均值大约是过去一段时间的平均值，因此我们用这个方法来计算二阶累积动量：，所以AdaBelta的参数更新公式为：

7. Adam/Nadam

讲到这，Adam和Nadam就很自然了： Adam = Adaptive + MomentumNadam = Nesterov + Adam 所以Adam的参数更新公式为：

Nadam的参数更新公式为：

其中有一个问题，Adam配合L2正则化的效果实际往往不如SGD，是因为二者实际上是相互冲突的。具体看下面带有L2正则化的Adam公式：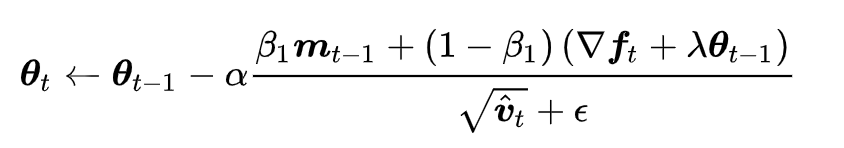

当二阶动量vt很大时，即梯度快速变化时，在这个方向上参数被正则化的很小，这是不合理的。即，Adam和L2正则是各项异性的，导致正则起不到作用，最终效果不好。于是产生了Adamw，bert就是采用Adamw方法优化参数，对除了layernorm，bias项之外的模型参数做weight decay。

上图，紫色对应Adam+L2，绿色对应Adamw。通过将红色项调整至绿色项，即在计算一阶二阶动量时加正则项，变为在实际参数更新时加正则项，以此来不让正则项被二阶动量所调整，完成快速梯度下降和L2权重衰减的解耦，保持各项同性，从而达到更好的效果。

8. SGD和Adam对比

1. 学术界在发论文时还有很多大牛只使用 SGD。(应用是应用，学术是学术)
2. Adam算法速度太快，有时不收敛，有时不能达到最优解。
3. SGD 虽然不那么“聪明”，但是它“单纯”。所有的控制都在你自己手中，用它才不会影响你对其它因素的研究。

   9. 可视化

   

   10. 高级优化算法

   10.1 线性回归模型求解方法

   虽说SGD是我们经常听说的优化方法，但实际工程中(sklearn)，常常会用另一种方法对线性回归模型进行求解，就是正规方程(normal equation)法，正规方程方法往往是更好的解决方案，他的具体做法是通过矩阵运算直接求得最优解，不再需要一次次迭代了：

   对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。

SGD与NE的优缺点比较：
梯度下降需要提前对各个特征进行特征缩放(归一化)，正规方程不需要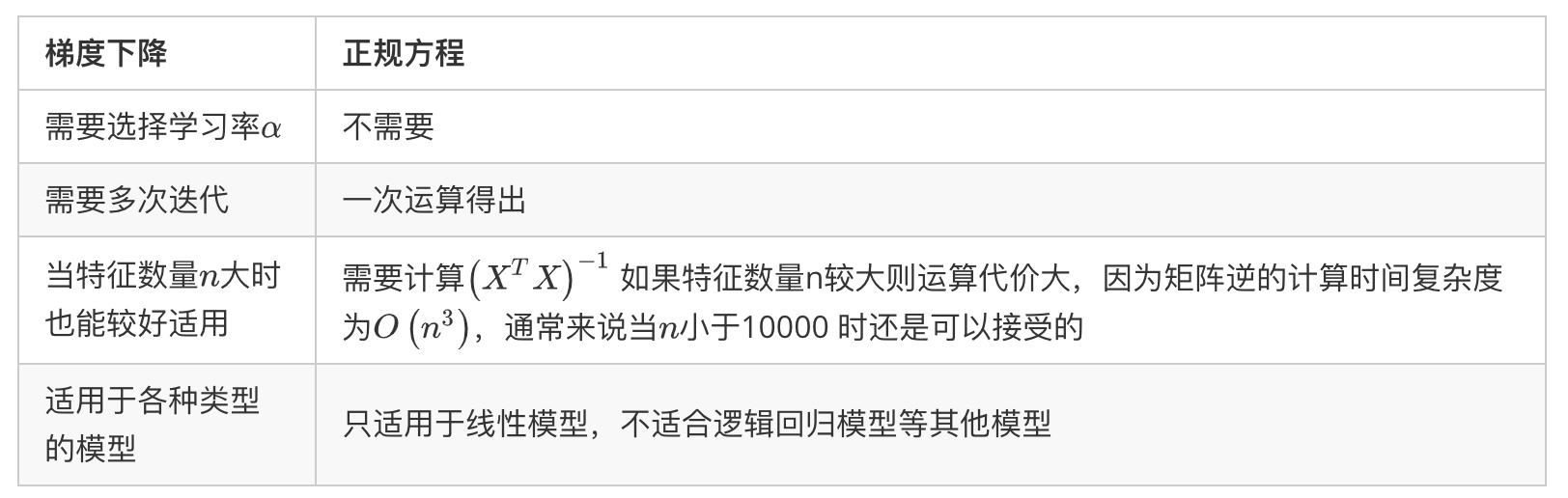

正规方程的python实现：

import numpy as np
def normalEqn(X, y): 
   theta = np.linalg.inv(X.T@X)@X.T@y     #X.T@X等价于X.T.dot(X)
   return theta

10.2 其他凸优化算法

共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法，它们需要有一种方法来计算，以及需要一种方法计算导数项，然后使用比梯度下降更复杂的算法来最小化代价函数。这些算法比较复杂，咱们直接跳过细节，看看他们的特性：

1. 不需要手动调节学习率，比梯度下降收敛得快得多。

   于这些算法的一种思路是，给出计算导数项和代价函数的方法，你可以认为算法有一个智能的内部循环，而且，事实上，他们确实有一个智能的内部循环，称为线性搜索(line search)算法，它可以自动尝试不同的学习速率 ，并自动选择一个好的学习速率 ，因此它甚至可以为每次迭代选择不同的学习速率，那么你就不需要自己选择。这些算法实际上在做更复杂的事情，不仅仅是选择一个好的学习速率，所以它们往往最终比梯度下降收敛得快多了，

2. 过于复杂。

   如果说这些算法有缺点的话，那么我想说主要缺点是它们比梯度下降法复杂多了，特别是你最好不要使用 L-BGFS、BFGS这些算法，除非你是数值计算方面的专家。 实际上大多数的论文都会使用梯度下降家族的算法，因为它更普世。

参考文献

1. 梯度下降法家族
2. 从 SGD 到 Adam —— 深度学习优化算法概览(一)
3. Adam 究竟还有什么问题 —— 深度学习优化算法概览(二)
4. 机器学习札记
5. 高等数学 第六版 上下册 —— 同济大学数学系编 高等教育出版社
6. 移动平均：你知道的与你不知道的