">
0. 从LR推演出NN的基础框架
我在另一篇博文中详细讲述了LR的相关细节，纯从计算顺序上来说，逻辑回归预测类别的顺序即：
- 输入样本
与模型参数
作内积，结果记为
；
- 将中间结果
输入到Sigmoid函数，输出为0到1之间的一个数
（在之前已经证明了这个
即其中一个类的后验概率）
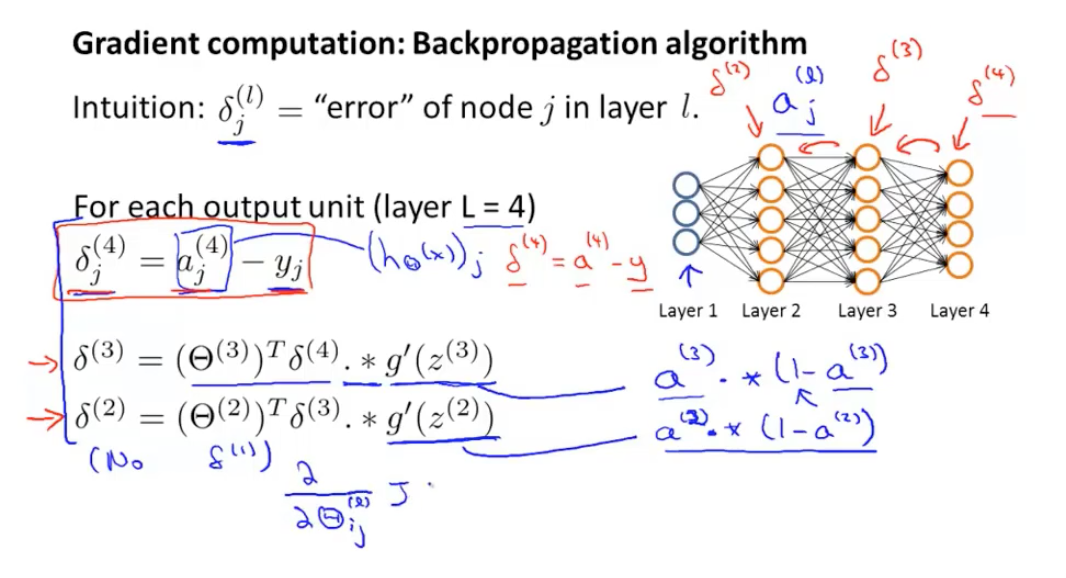
咱们把它想象的画出来一下(注意下面的图文均省略了偏置项没但这并不代表它不重要！)：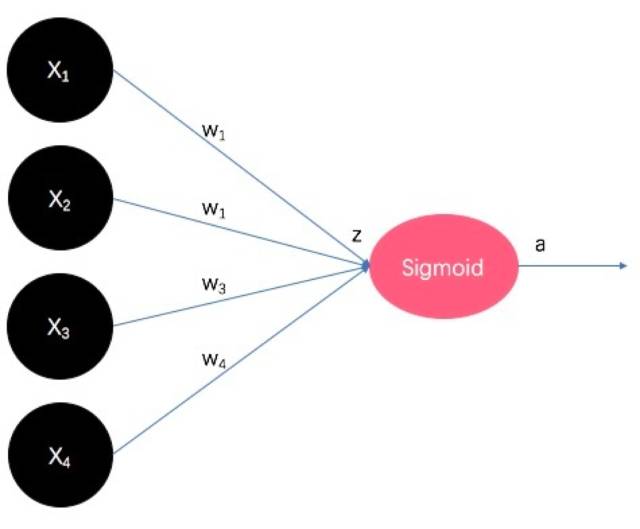
黑色圈圈代表原始的输入，即4维的特征向量。连接边代表模型参数
，图片里用
表示，代表weight，即特征向量每一维度的权重。权重的末端即
与
的内积结果
，也是Sigmoid函数的输入。输入
经过Sigmoid函数非线性映射后生成
，即某一类别的后验概率。看出来了么，这其实就是最早的可以看作为只有输入和输出，没有隐藏层的神经网络啊！
咱们再发展一下思维，对于二分类任务，我们如果将多个逻辑回归分类器的输出，作为另一个逻辑回归分类器的输入，并让这个逻辑回归分类器负责输出分类任务的类别。比如我们用3个逻辑回归分类器的输出作为另1个逻辑回归分类器的输入：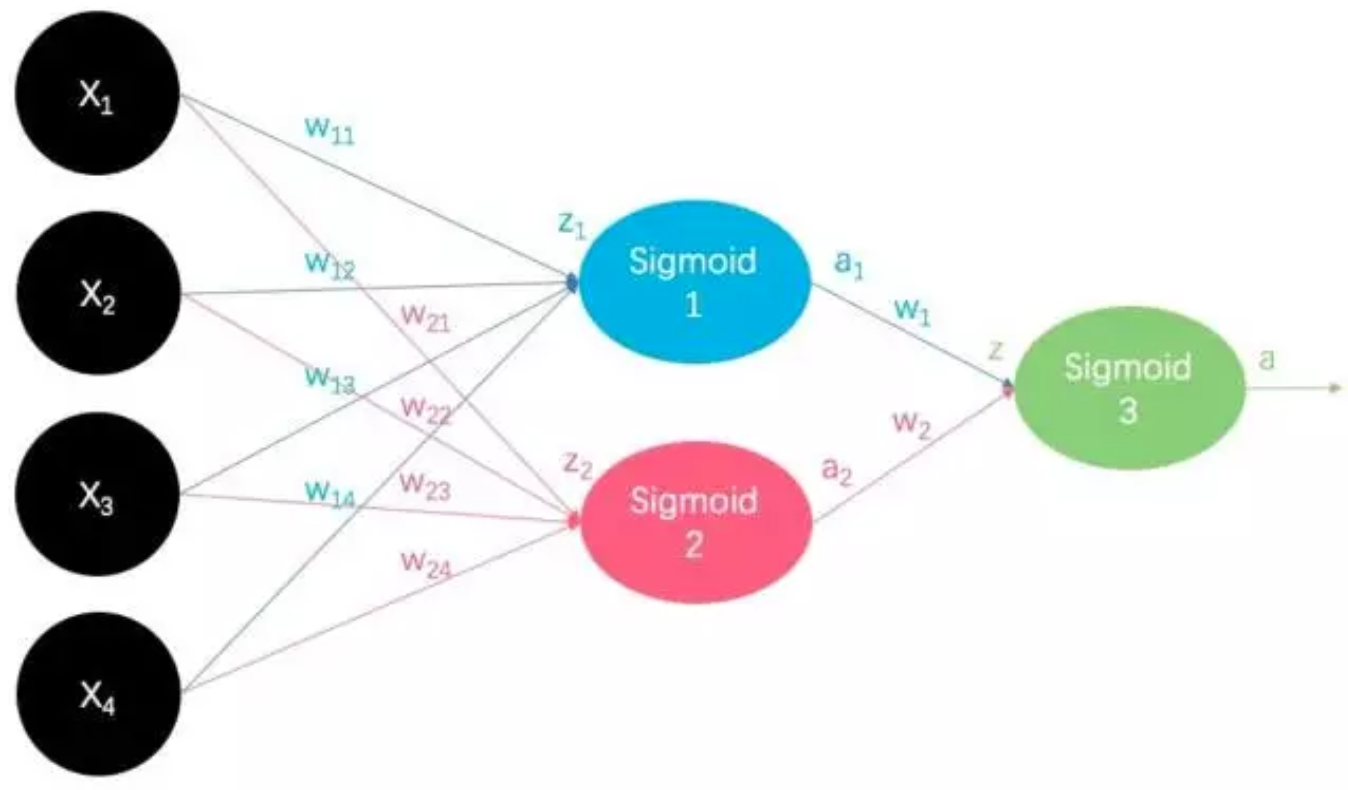
这不就是神经网络嘛！所以说，神经网络其实也是将LR模型多来叠加几层，只不过在非线性映射激活函数的选取上更多变了一些，仅此而已。中间的这两个所谓的LR模型就是神经网络中的隐藏层，至于他们输出的到底代表了什么，至今未解，这就是大名鼎鼎的NN黑盒，虽然里面黑(难以经过严格数学解释其输出)，但其最终的输出分类效果还是很好的。
问题来了，为什么使用这种结构？
对于单个LR分类器来说，它只能解决线性可分的数据集，而且不同的LR模型学到的决策面是不同的：
如果咱们采用神经网络结构，即将这两个LR结果合起来再作为一个LR模型的输入，进行输出：
这时候我们就相当于变相的把原来线性不可分的数据映射到另一个坐标维度上，而在那个维度上是线性可分的，从而最终在二维上显示的就是我们很好地把数据分隔开了！
好了，说完了，这就是LR和NN的密切联系，归根到底它们基础的思想是几乎一样的。
下面大致回顾一下NN的发展历程：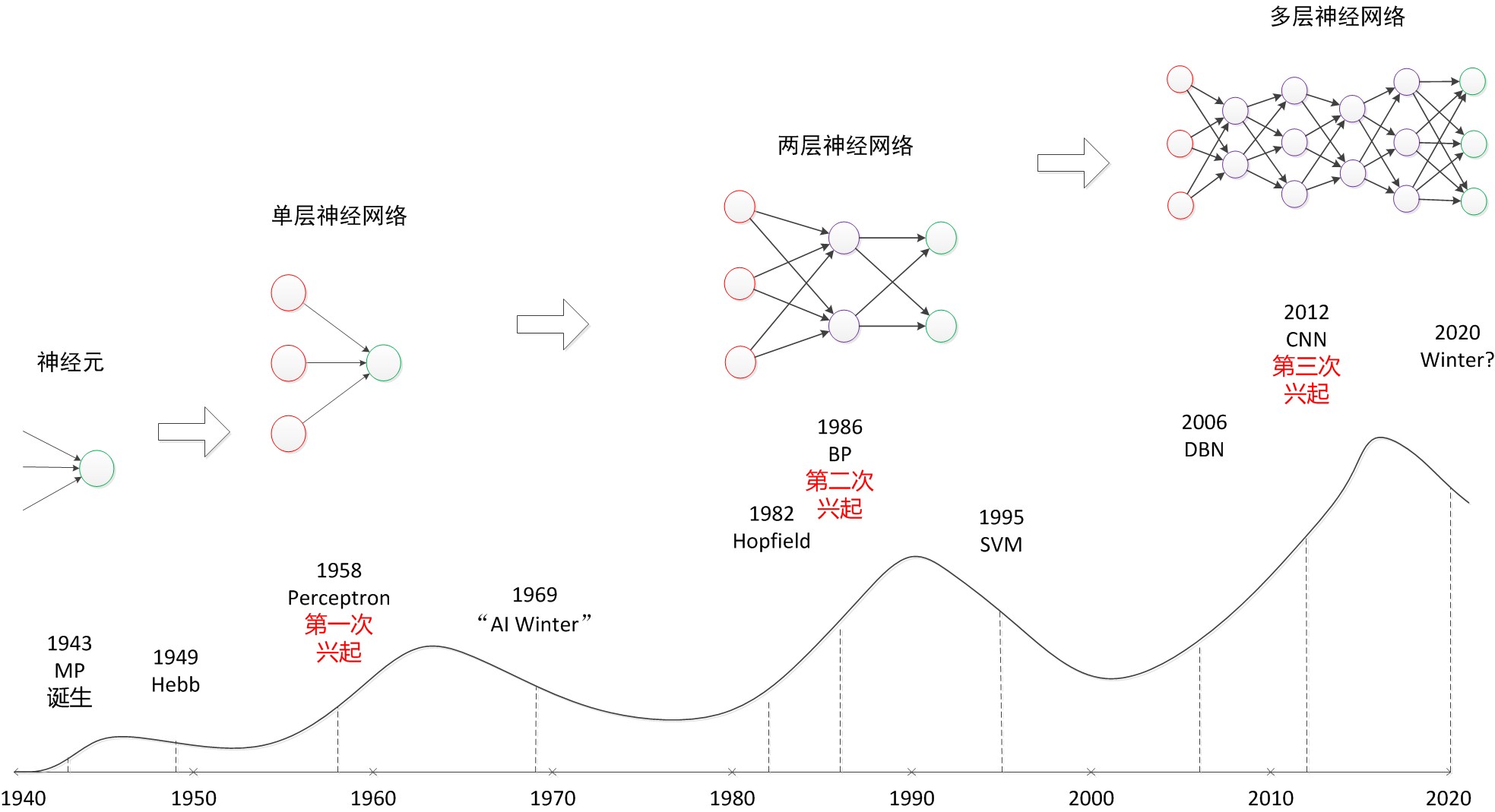
历史总是惊人的相似，NN同样经历过不同的低估和兴起，目前刚好它应该属于最顶峰的时刻。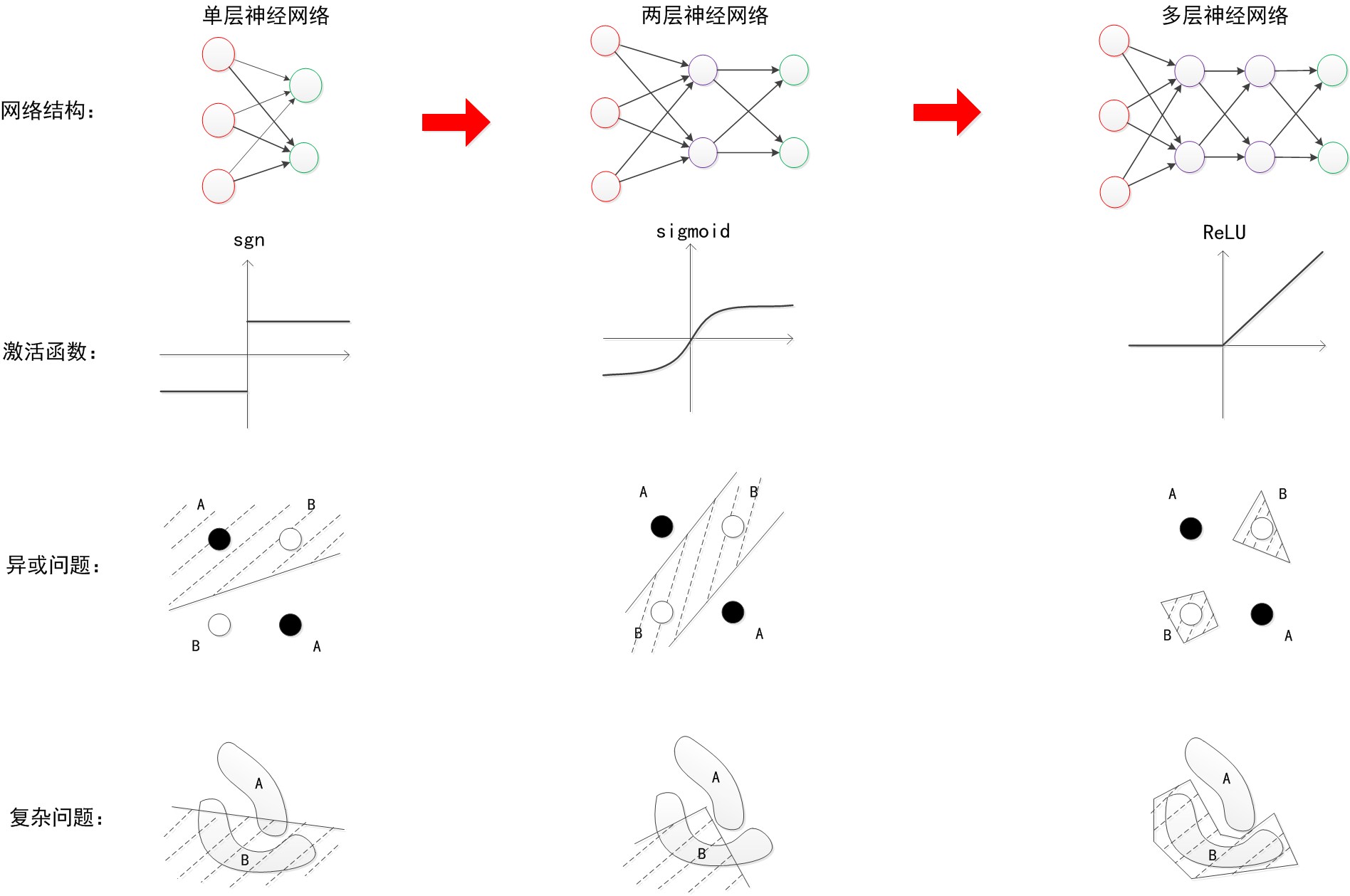
可以看出，随着层数增加，其非线性分界拟合能力不断增强。图中的分界线并不代表真实训练出的效果，更多的是示意效果。神经网络的研究与应用之所以能够不断地火热发展下去，与其强大的函数拟合能力是分不开关系的。
1. NN中的偏置项
上述阐述过程中均忽略的偏置项，但它其实是非常重要的，很多人不明白为什么要在神经网络、逻辑回归中要在样本X的最前面加一个1，使得 X=[x1,x2,…,xn] 变成 X=[1,x1,x2,…,xn] 。因此可能会犯各种错误，比如漏了这个1，或者错误的将这个1加到W·X的结果上，导致模型出各种bug甚至无法收敛。究其原因，还是没有理解这个偏置项的作用
我们知道，逻辑回归模型本质上就是用 y=WX+b 这个函数画决策面，其中W就是模型参数，也就是函数的斜率（回顾一下初中数学的 y=ax+b ），b就是函数的截距。如果没有这个偏置项b，那么我们就只能在空间里画过原点的直线/平面/超平面。这时对于绝大部分情况，比如下图，要求决策面过原点的话简直是灾难。
因此，对于逻辑回归来说，必须要加上这个偏置项b，配合其中的斜率，才能保证我们的分类器可以在空间的任何位置画决策面。当然前面说了，神经网络本质就是一层层的多个相当于LR分类器的模型，所以偏置的作用也大同小异了，不过有一点需要注意。如何为不同分类器(隐节点)分配不同的b呢？或者说如果让模型在训练的过程中，动态的调整不同分类器的b以画出各自最佳的决策面呢？
那就是先在X的前面加个1，作为偏置项的基底，（此时X就从n维向量变成了n+1维向量，即变成 [1, x1,x2…] ），然后，让每个分类器去训练自己的偏置项权重，所以每个分类器的权重就也变成了n+1维，即[w0,w1,…]，其中，w0就是偏置项的权重，所以1*w0就是本分类器的偏置/截距啦。这样，就让截距b这个看似与斜率W不同的参数，都统一到了一个框架下，使得模型在训练的过程中不断调整参数w0，从而达到调整b的目的。 注意NN里面涉及到两个偏置，一个是某一层的偏置项，另一个是节点内部的偏置项(相当于LR模型中的偏置项)。
2. NN的训练和BP
2.1 BP原理
所谓神经网络的训练或者是学习，其主要目的在于通过学习算法得到神经网络解决指定问题所需的参数，这里的参数包括各层神经元之间的连接权重以及偏置等。因为作为算法的设计者（我们），我们通常是根据实际问题来构造出网络结构，参数的确定则需要神经网络通过训练样本和学习算法来迭代找到最优参数组。
神经网络的学习算法中最杰出成功的代表当属误差逆传播（error BackPropagation，简称BP）算法，BP学习算法通常用在最为广泛使用的多层前馈神经网络中。
BP算法其实并不是一个独立的优化算法，它的本质其实是能够更快更有效的计算损失函数关于不同参数的梯度(偏导)
首先咱们先普及一下导数的链式法则(chain rule)：
咱们一步一步来，首先计算损失函数
关于某项参数
的梯度(偏导)如下：
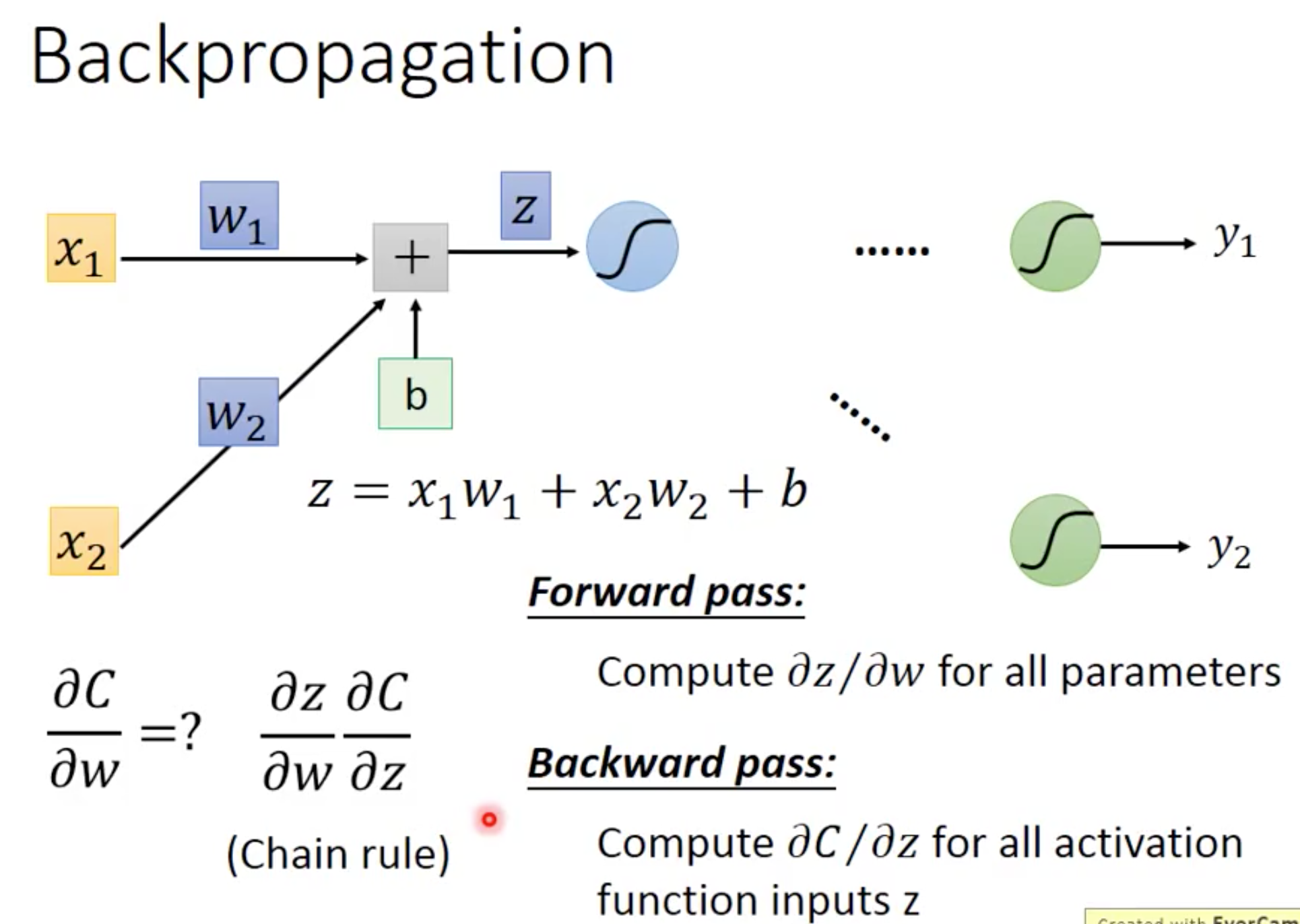
接着继续展开forward 和 backward pass部分：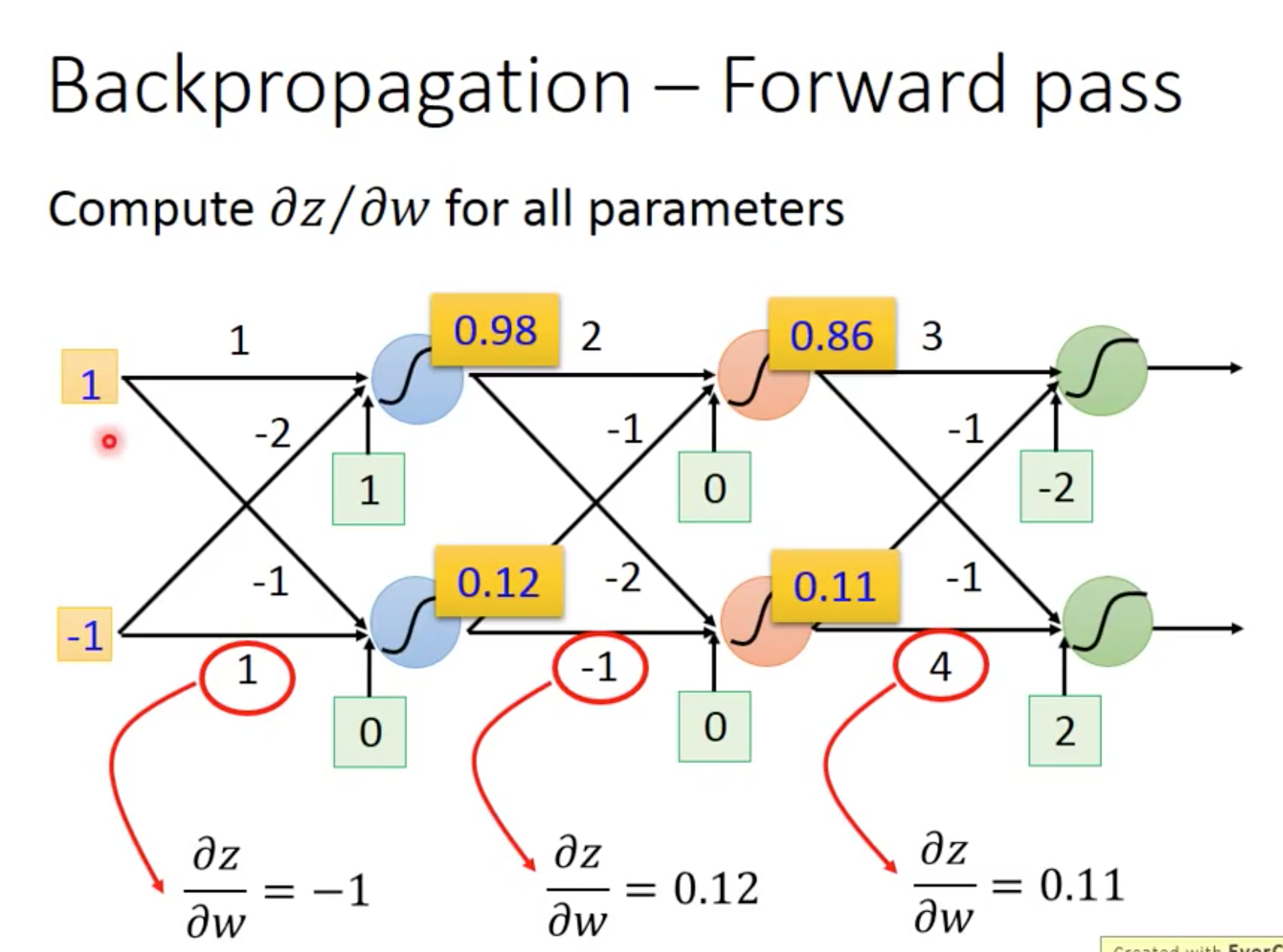
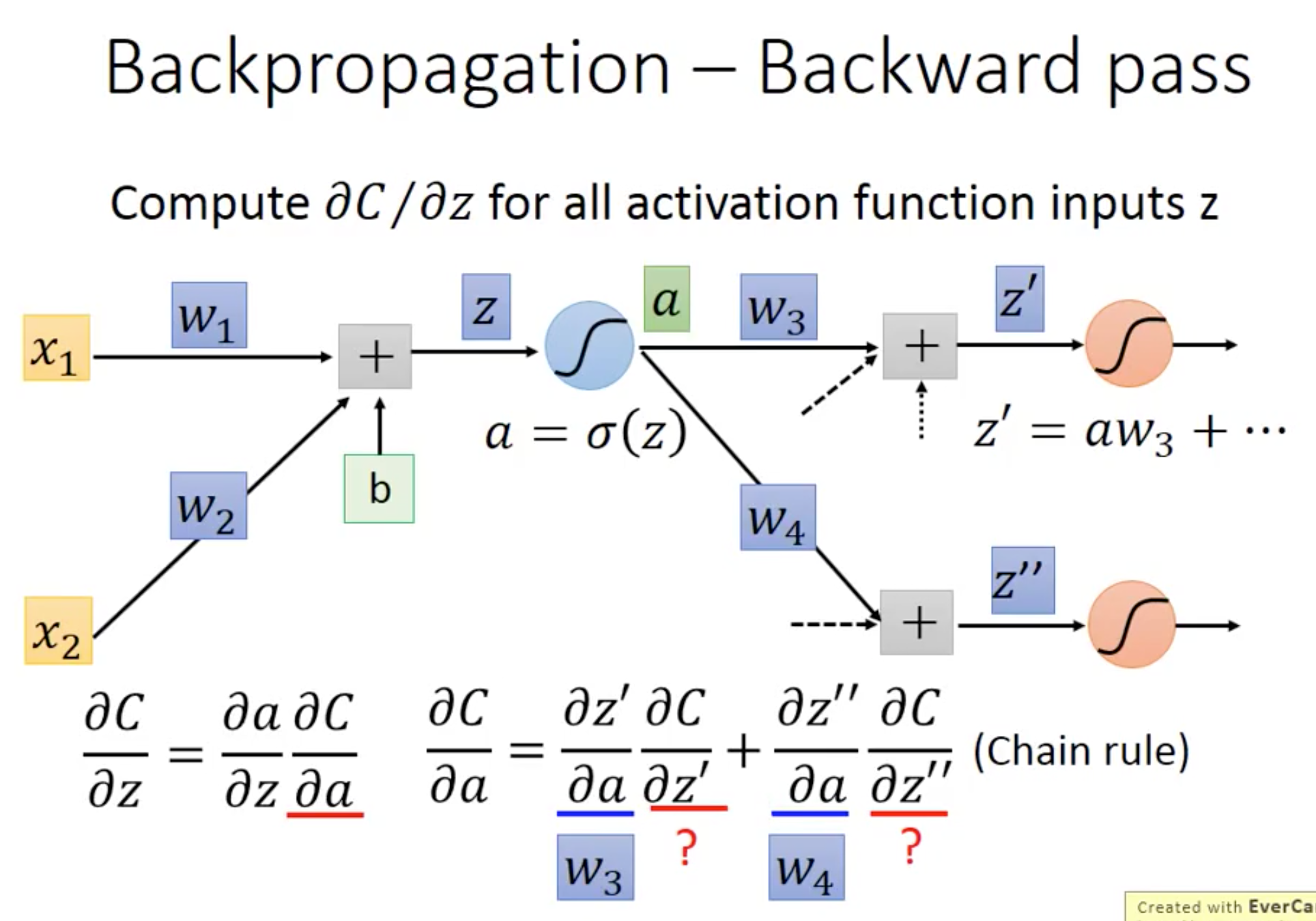
其中backward pass中对
的计算是重中之重，也是BP算法的真正由来：
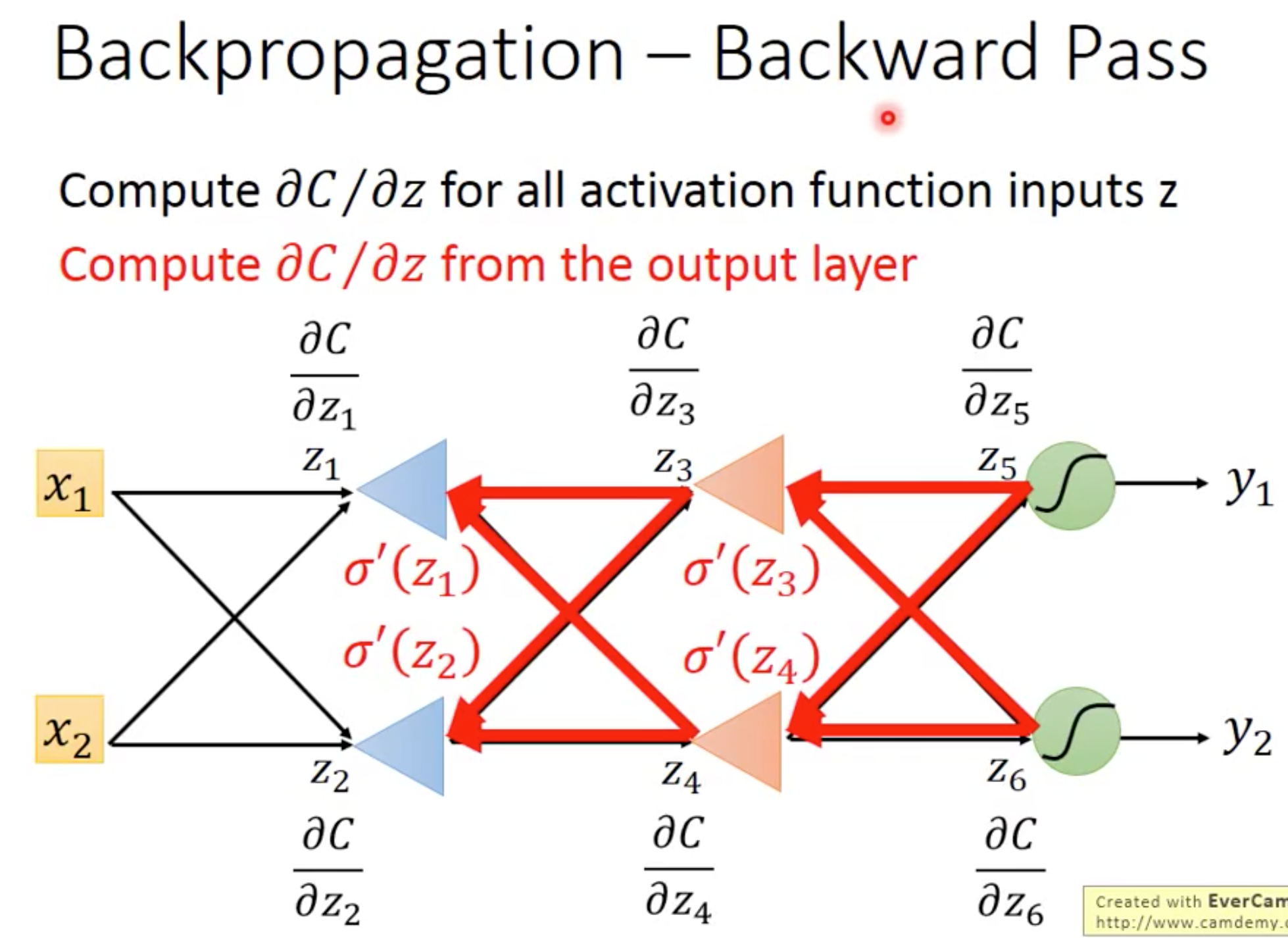
我们对前一层某个
的计算需要知道后面一层全部的
，这就和斐波那契数列本质相同，我们利用自底向上的动态规划方法来优化这种运算，就和BP步骤一模一样了。
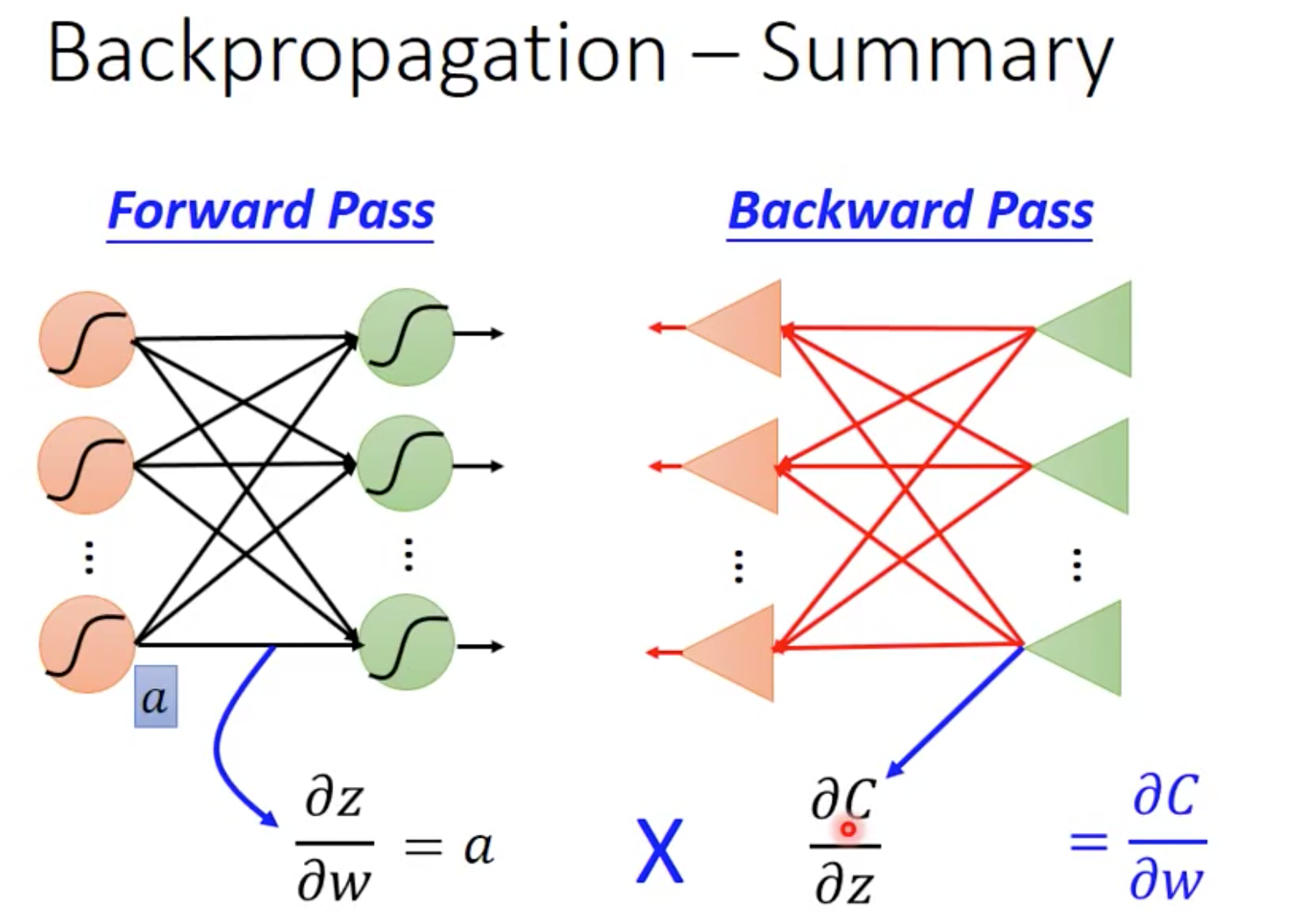
这样就明了多了，整合一下咱们的BP算法具体流程：
2.2 梯度数值检测(Numerical Gradient Checking)
当我们对一个较为复杂的模型（例如神经网络）使用梯度下降算法时，可能会存在一些不容易察觉的错误，意味着，虽然代价看上去在不断减小，但最终的结果可能并不是最优解。
为了避免这样的问题，我们采取一种叫做梯度的数值检验（Numerical Gradient Checking）方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。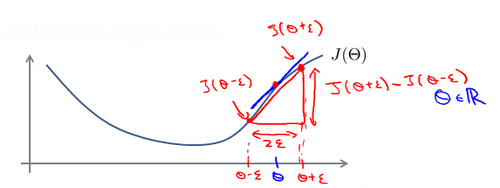
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的
，我们计算出在
处和
的代价值（是一个非常小的值，通常选取
），然后求两个代价的平均，用以估计在
处的代价值。
当是
一个向量时，我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对一个参数的改变进行检验，最后我们还需要对通过反向传播方法计算出的偏导数进行检验。根据上面的算法，计算出的偏导数存储在
矩阵中，检验时，我们要将该矩阵展开成为向量，同时我们也将
矩阵展开为向量，我们针对每一个
都计算一个近似的梯度值，将这些值存储于一个近似梯度矩阵中，最终将得出的这个矩阵同
进行比较。
2.3 随机初始化
任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0，这样的初始方法对于逻辑回归来说是可行的，但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0，这将意味着我们第二层的所有激活单元都会有相同的值。同理，如果我们初始所有的参数都为一个非0的数，结果也是一样的。
所以在NN中的参数初始化一定是随机的，但是LR模型中则不必，可以随机初始化为0。因为之前我在这篇博文中也讲过了LR和NN的关系：
逻辑回归可以看作是只有n个神经元的单层神经网络，神经网络就是一组神经元连接在一起的网络，隐藏层可以有多个神经元，每个神经元本身就对应着一个逻辑回归过程。
Logistic回归没有隐藏层，如果将权重初始化为零，则Logistic回归中的第一个示例x将输出零，但Logistic回归的导数取决于不是零的输入x（因为没有隐藏层）。 因此，在第二次迭代（迭代发生在w和b值的更新中，即梯度下降）中，如果x不是常量向量，则权值遵循x的分布并且彼此不同。这也是我在另一篇博文z中提到的BN的的重要思想来源(输入数据的分布一致性)。
2.4 完整训练过程
把之前的零散重点全部顺序整合在一起，NN的训练过程如下：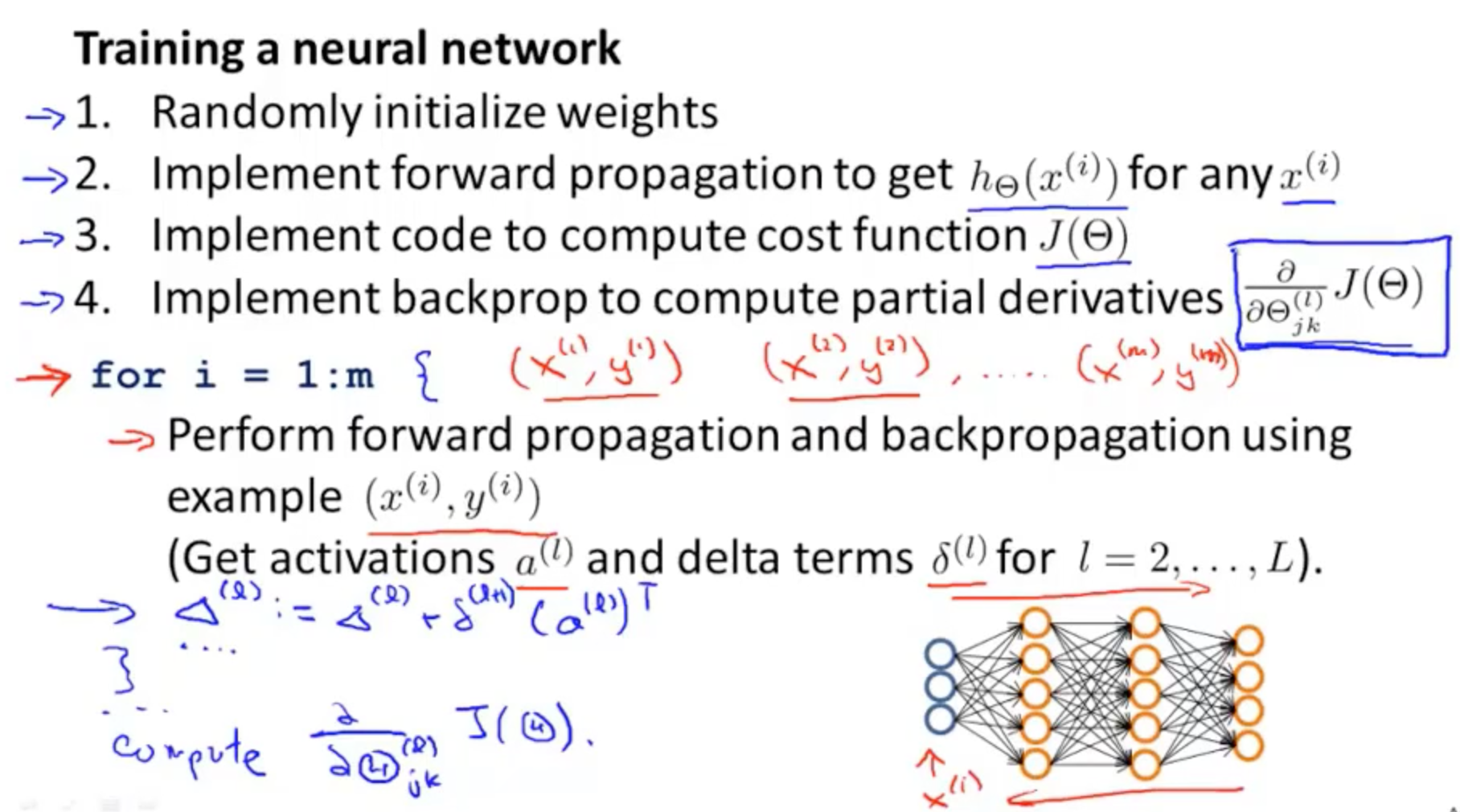
对应的pytorch实现流程如下：
def train(dataloader, model, loss_fn, optimizer): size = len(dataloader.dataset) model.train() for batch, (X, y) in enumerate(dataloader): X, y = X.to(device), y.to(device)
# Compute prediction errorpred = model(X) # 前向传播更新网络节点值，并得到最终输出loss = loss_fn(pred, y) # 根据最终输出和groundtruth计算loss# Backpropagationoptimizer.zero_grad() # 参数梯度置为0loss.backward() # 反向传播，根据loss计算梯度计算batch的累积参数梯度optimizer.step() # 参数更新，根据计算的梯度进行更新if batch % 100 == 0:loss, current = loss.item(), batch * len(X)print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
以两个参数的三维训练过程可视化如下(在二维可以可视化为等高线形式)：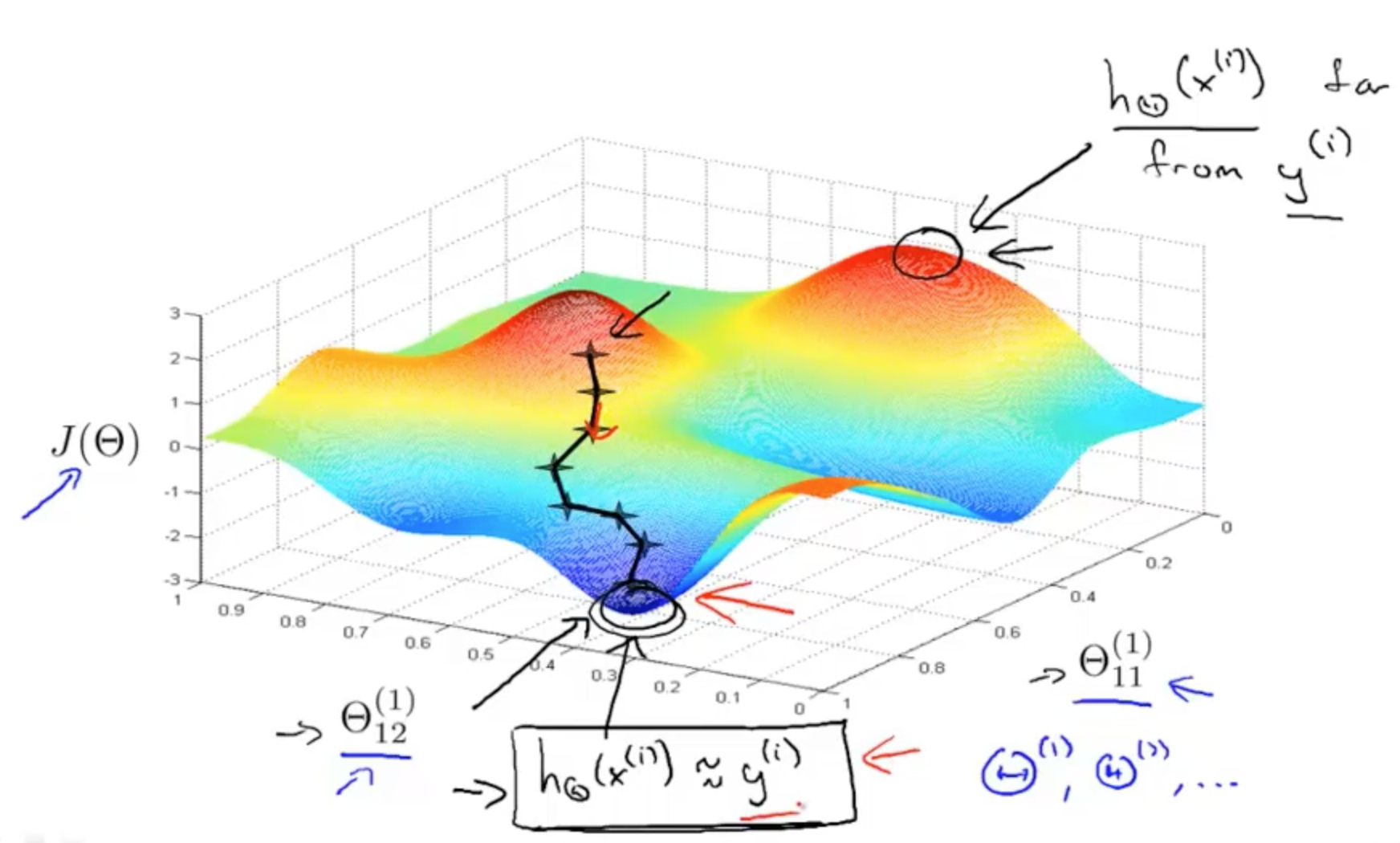
3. 分清一下前馈NN和反馈NN
- 前馈和BP真没什么关系，前馈是前馈，BP是BP，前馈谈论的是模型，BP是一种算法，用于训练网络；
- 前馈神经网络（FNN）是相对循环神经网络（RNN）而言的；
- FNN和RNN的区别在于，FNN只能前馈，RNN存在反馈：前馈是说信号在各层之间只能向前传递，跳阶都行，只要它向前传而不是向后传；而反馈是指信号不仅可以向前传，还可以向后传，这就构成了环路，故“循环”；
- FNN可以是FNC、CNNs(VGG,ResNet,DenseNet)等 ，RNN可以是LSTM等变体。
3. 梯度爆炸，消失，弥散
3.1 本质原因
层数比较多的深层神经网络模型在训练时会出现梯度消失问题（gradient vanishing problem）和梯度爆炸问题（gradient exploding problem）。梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。
例如，对于下图所示的含有3个隐藏层的神经网络，梯度消失问题发生时，接近于输出层的hidden layer 3的权值更新相对正常，但前面的hidden layer 1的权值更新会变得很慢，导致前面的层权值几乎不变，仍接近于初始化的权值，这就导致hidden layer 1相当于只是一个映射层，对所有的输入做了一个同一映射，这时此深层网络的学习就等价于只有后几层的浅层网络的学习了。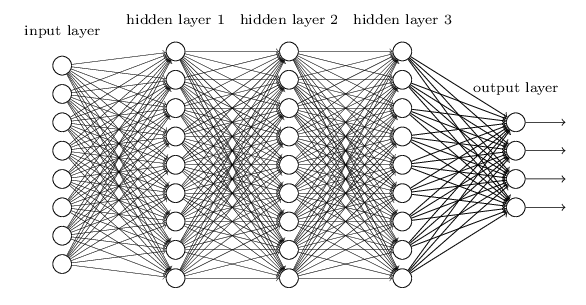 
而产生这种原因主要是因为BP算法的原理，前面我已经对其进行了详细剖析，这里再简单回顾一下，
而sigmoid的函数的导数如下，它的取值范围为
，随意随着层数加深，偏导数会越来越小，最终趋近于0，这就是梯度消失的本质原因，当然梯度爆炸和它类似，只不过激活函数的导数取值是大于1的范围：
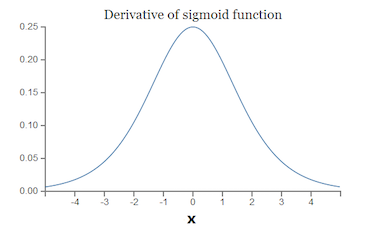
从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多，这种现象就叫做梯度弥散。因此，梯度消失、爆炸和弥散的根本原因在于反向传播训练法则，属于先天不足，另外多说一句，Hinton提出capsule的原因就是为了彻底抛弃反向传播，具体细节可以参考我的另一篇博文。
3.2 解决方法
预训练加微调
此方法来自Hinton在2006年发表的一篇论文，Hinton为了解决梯度的问题，提出采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-tunning）。Hinton在训练深度信念网络（Deep Belief Networks中，使用了这个方法，在各层预训练完成后，再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优，此方法有一定的好处，但是目前应用的不是很多了。
梯度剪切、正则化权重(针对梯度爆炸)
梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。 正则化是通过对网络权重做正则限制过拟合
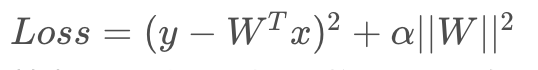其中，α\alphaα是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。使用不同的激活函数
使用relu、elu等函数代替sigmoid函数作为神经元的激活函数，具体函数特性我会在下一小节进行详细讲解。
使用Normaliazation
Norm是很重要的工作，它通过规范化操作将输出信号x规范化保证网络的稳定性。具体细节可以参考我的另一篇博文。
使用残差机制
事实上，就是残差网络的出现导致了image net比赛的终结，自从残差提出后，几乎所有的深度网络都离不开残差的身影，相比较之前的几层，几十层的深度网络，在残差网络面前都不值一提，残差可以很轻松的构建几百层，一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分，其中残差单元如下图所示：
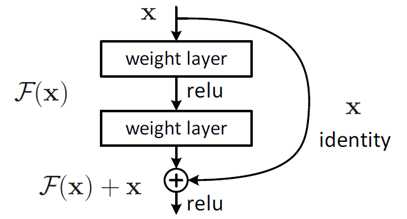相比较于以前网络的直来直去结构，残差中有很多这样的跨层连接结构，这样的结构在反向传播中具有很大的好处，具体细节可以参考我的另一篇博文。使用LSTM网络机制
LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，如下图，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。目前也有基于CNN的LSTM，具体细节可以参考我的另一篇博文
参考文献
若有收获，就点个赞吧
0 人点赞
