review PCA降维

Principal component analysis（主成分分析）

0. 数学理论推导

0.1 向量内积与投影

内积运算将两个向量映射为一个实数，有两种形式：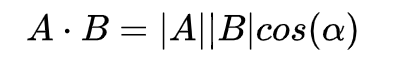


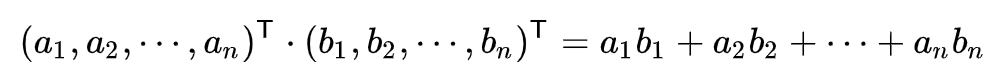
其几何意义为

A与B的内积值等价于A向B所在直线投影的矢量长度(设向量B的模为1)

0.2 基与基变换

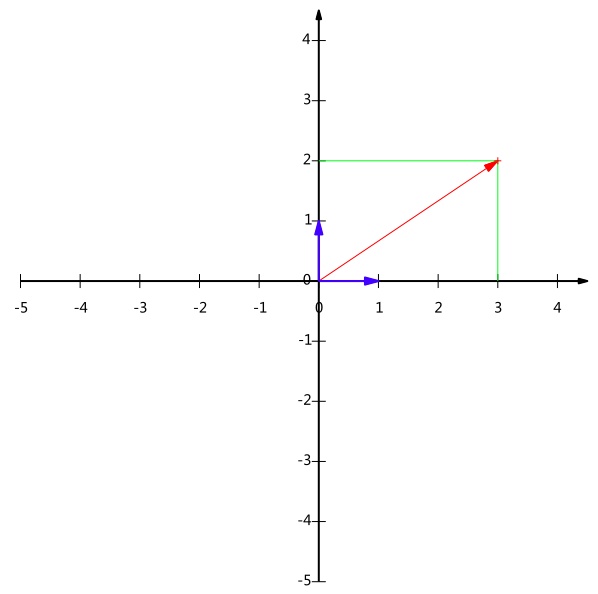
要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值。上述向量用(3,2)表示，以(1,0)和(0,1)为基。

• 为方便通常均默认以(1,0)和(0,1)为基，实际上任何两个线性无关的二维向量都可以成为一组基，所谓线性无关在二维平面内可以直观认为是两个不在一条直线上的向量。
• 我们希望基的模是1，因为从内积的意义可以看到，如果基的模是1，那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了。
• 我们列举的例子中基均是正交的（即内积为0，或直观说相互垂直），但可以成为一组基的唯一要求就是线性无关，非正交的基也是可以的。不过因为正交基有较好的性质，所以一般使用的基都是正交的。

下面我们通过矩阵形式一步到位来进行基变换：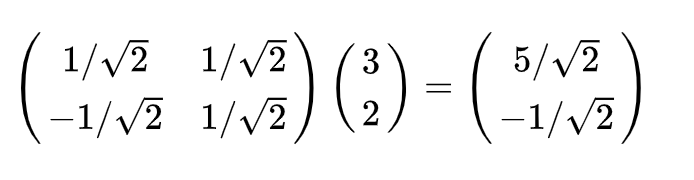

其中矩阵的两行分别为两个基，乘以原向量，其结果刚好为新基的坐标，类似的我们可以推广到任意数量的任意维向量。
如果我们有M个N维向量，想将其变换为由R个基向量表示的新空间中：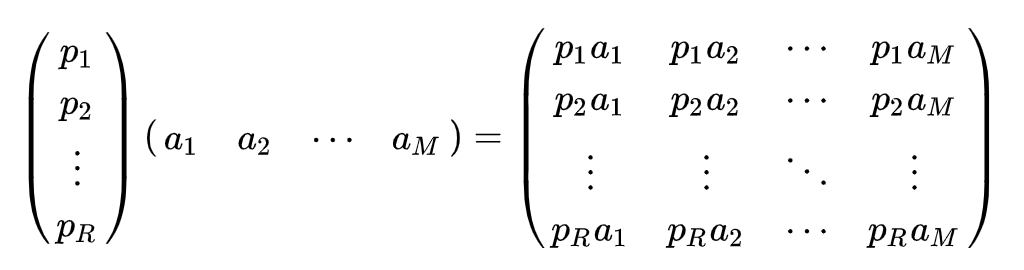

其中Pi是一个行向量，表示第i个基，aj是一个列向量，表示第j个原始数据记录。

上述分析同时给矩阵相乘找到了一种物理解释： 两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。

0.3 协方差矩阵及优化目标

如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该如何选择K个基才能最大程度保留原有的信息？
一种直观的看法是：希望投影后的投影值尽可能分散，即投影后方差最大化：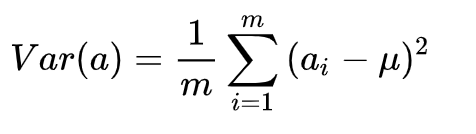

在处理数据时，我们先将数据进行去中心化处理，即将每个字段(特征)内所有值都减去该字段整体均值，其结果是将每个字段都变为均值为0，这样方差就会进一步转化为：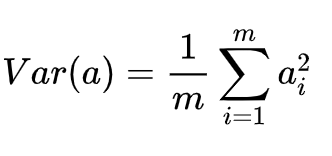

当然还有另一约束条件：从直观上说，让两个字段尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个字段不是完全独立，必然存在重复表示的信息，即要保证不同的基之间正交，即协方差为0。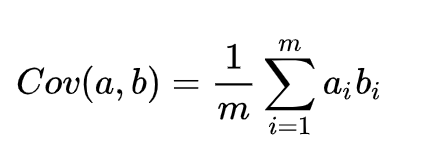

综上所述，优化目标即为：
将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。

0.4 协方差矩阵及对角化

上节给出了优化目标的直观解释，下面来进行一下严格的数学上的优化方案。
假设我们只有a和b两个字段，那么我们将它们按行组成矩阵X：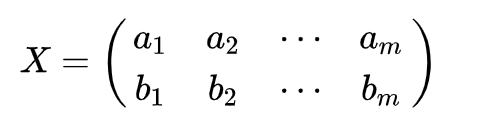

然后我们用X乘以X的转置，并乘上系数1/m：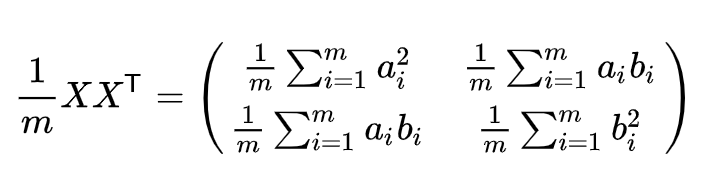

这就是协方差矩阵的由来，协方差矩阵能够将上述两个优化目标(协方差和方差)很好地囊括在其中。协方差矩阵对角线上的两个元素分别是两个字段的方差，而其它元素是a和b的协方差，二者被这样被统一到了一个矩阵中，神不神奇，谁还敢说高数，线性代数没用？
所以优化目标进一步等价为将协方差矩阵对角化，即除对角线外的其它元素化为0，并且在对角线上将元素按大小从上到下排列，这样我们就达到了优化目的。
设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：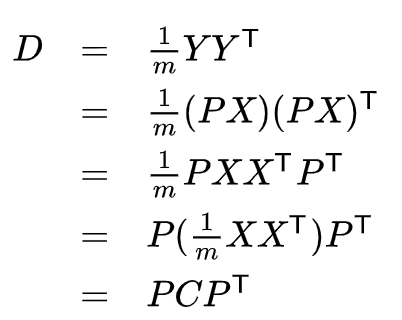

换句话说，优化目标变成了寻找一个矩阵P，满足是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。
进一步通过奇异值分解我们就可以求出P矩阵了。

1. 算法步骤

总结一下，PCA的算法步骤：

1. 将原始数据按列组成n行m列矩阵X，并进行均值归一化(还可以进行特征缩放)

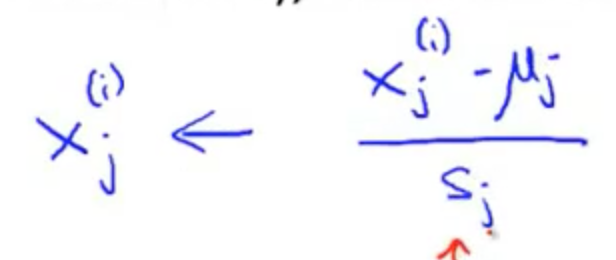
1. 求出协方差矩阵：
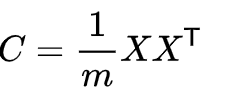
2. 求出奇异值分解后的P矩阵：求出协方差矩阵的特征值及对应的特征向量，将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P

3. Y=PX即为降维到k维后的数据

   2. PCA特点

4. PCA是一种无参数技术，也就是说面对同样的数据，如果不考虑清洗，谁来做结果都一样，没有主观参数的介入，所以PCA便于通用实现，但是本身无法个性化的优化。

5. PCA也存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关，关于这点就不展开讨论了。另外，PCA假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA的效果就大打折扣了。

   3. PCA使用常见错误

6. 一个常见错误使用主要成分分析的情况是，将其用于减少过拟合（减少了特征的数量）。这样做非常不好，不如尝试正则化处理。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。然而当我们进行正则化处理时，会考虑到结果变量，不会丢掉重要的数据。

7. 另一个常见的错误是，默认地将主要成分分析作为学习过程中的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主要成分分析。

   参考文献

   1. PCA的数学原理(转)