0. 理论总结
- 进化路程:递归->记忆搜索->动态规划->动态规划+枚举->动态规划+枚举+压缩
- 递归实现的代码简洁易懂,但是需要注意的是,递归由于是函数调用自身,而函数调用是有时间和空间的消耗的,每一次函数调用,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,而往栈里压入数据和弹出数据都需要时间,因而递归实现的效率最差。
- 递归中有很多不必要的重复计算,我们可以采用一个固定的数组记录计算过的数据,当再次遇到就不必计算,这样可以较少递归的时间复杂度
- 动态规划和记忆搜索类似,只不过动态规划是自底向上的,而记忆搜索是自顶向下的(与递归相同);
- 有些问题动态规划还可以进一步通过枚举和空间压缩来优化
1. 斐波那契一系列题型(leetcode_70)**
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数。
输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
此题有三种解法:
- 自顶向下递归解法
- 自顶向下记忆搜索法
- 自底向上动态规划法
这题属于最经典的斐波那契形式的问题,先利用递归形式进行编程:
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""if n < 0:return -1elif n == 0 or n == 1:return 1else:return self.climbStairs(n-1) + self.climbStairs(n-2)
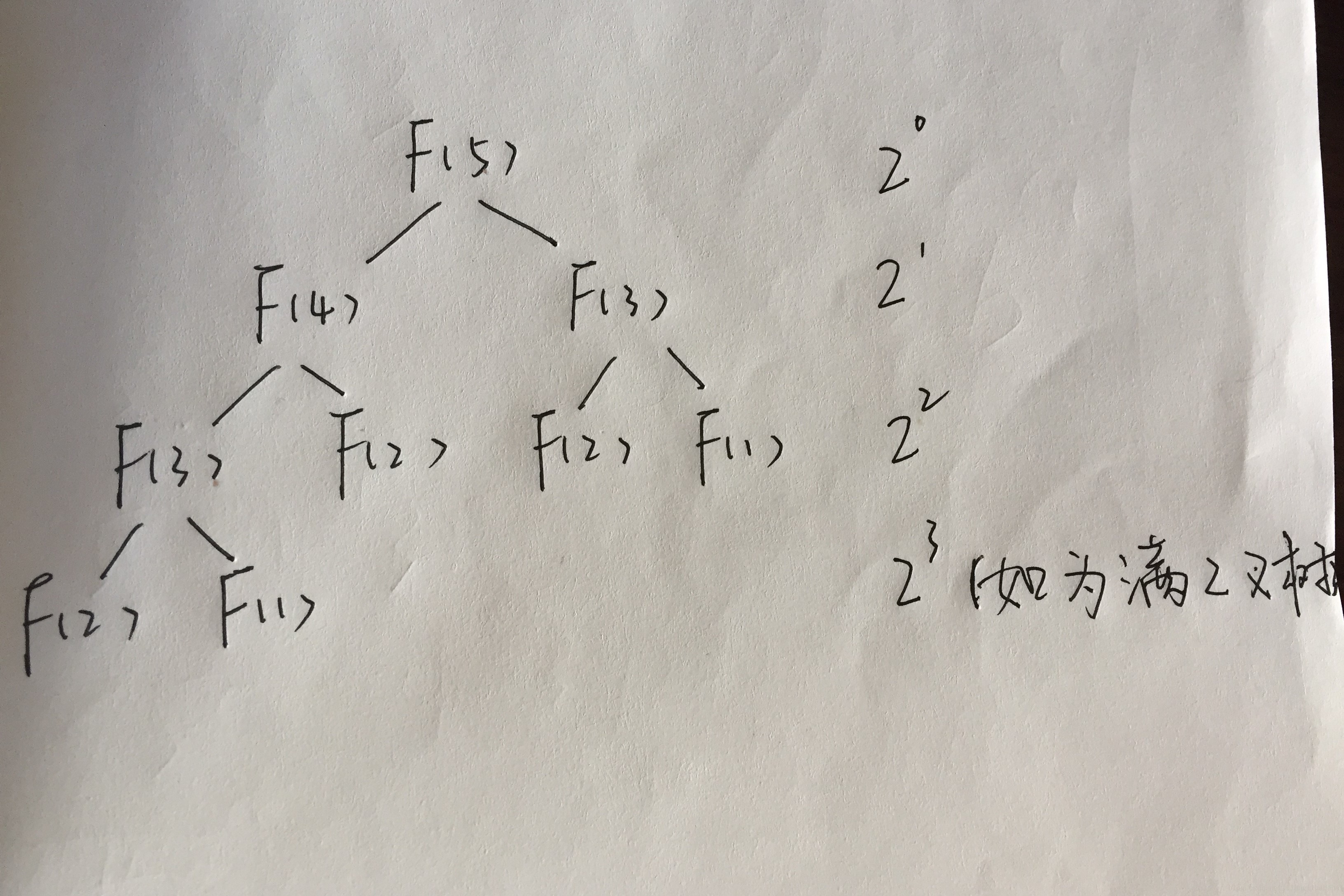
递归算法的时间复杂度为二叉树节点个数:,空间复杂度为树的高度:
即
。这里可以小小复习一下满二叉树的节点数,等差等比数列性质(求和公式)。
再利用自顶向下记忆搜索的方式求解,将上述二叉树中不必要的重复计算模块记忆存储起来,避免重复运算:
class Solution(object): def climbStairs(self, n): """ :type n: int :rtype: int """ temp = [0 for i in range(n+1)] temp[0], temp[1] = 1, 1 return self.pro(n, temp) def pro(self, n, temp): if n < 0: return -1 elif n == 0 or n == 1: return 1 if temp[n-1] != 0 and temp[n-2] != 0: return temp[n-1] + temp[n-2] elif temp[n-1] != 0: temp[n] = self.pro(n-2, temp) + temp[n-1] return temp[n] else: temp[n] = self.pro(n-1, temp) + self.pro(n-2, temp) return temp[n]时间复杂度:
,空间复杂度:
在进一步利用自底向上的动态规划方式:
class Solution(object): def climbStairs(self, n): """ :type n: int :rtype: int """ if n < 0: return -1 elif n == 0 or n == 1: return 1 else: dp = [0 for i in range(n+1)] dp[0], dp[1] = 1, 1 for i in range(2, n+1): dp[i] = dp[i-1] + dp[i-2] return dp[-1]时间复杂度:
,空间复杂度:
更进一步对动态规划进行空间压缩,我们会发现仅用常数个变量就可以完成:
class Solution(object): def climbStairs(self, n): """ :type n: int :rtype: int """ if n < 0: return -1 elif n == 0 or n == 1: return 1 else: first, second = 1, 1 for i in range(2, n+1): res = first + second first, second = second, res return res时间复杂度:
,空间复杂度:
还有更精简的方法,利用矩阵乘法可以将时间复杂度减少至
,此方法过于偏,暂不细述。
与该题类似的题目:
假设农场中成熟的母牛每年只会生3头小牛,并且永远不会死。第一年农场有1只成熟的母牛,从第二年开始,母牛开始生小牛。每只小牛3年之后成熟又可以生小母牛。给定整数N,求N年后牛的数量。
2. 矩阵最小路径和(leetcode_64)
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。每次只能向下或者向右移动一步。
输入: [[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
*进阶思考:**若数组中数字不是非负,而是任意数,怎么办?
核心递归思想分析:
其中代表从左上角到L[x][y]位置的最小路径和,L为输入的矩阵。
核心递归思想明确了,编程其实就只是翻译的工作了,不过依然有四种形式的方法,递归、记忆搜索、动态规划,压缩动态规划。
递归方法, 时间复杂度
,空间复杂度
,其中X,Y分别为二维矩阵的维度:
#递归方法 class Solution(object): def minPathSum(self, grid): """ :type grid: List[List[int]] :rtype: int """ x, y = len(grid)-1, len(grid[0])-1 return self.pro_recur(x, y, grid) def pro_recur(self, x, y, grid): if x == 0 and y == 0: return grid[x][y] elif x == 0: return self.pro_recur(x, y-1, grid) + grid[x][y] elif y == 0: return self.pro_recur(x-1, y, grid) + grid[x][y] else: return min(self.pro_recur(x, y-1, grid), self.pro_recur(x-1, y, grid)) + grid[x][y]记忆搜索方法,时间复杂度为
,空间复杂度为
:
class Solution(object): def minPathSum(self, grid): """ :type grid: List[List[int]] :rtype: int """ x, y = len(grid), len(grid[0]) temp = [[-1 for i in range(y)] for j in range(x)] return self.pro_recur(x-1, y-1, grid, temp) #如果temp某位置为-1则表示相应位置未计算过,需递归计算;否则表明该位置计算过并存储在temp数组中,此时就不必计算了,直接从数组中取值即可。 def pro_recur(self, x, y, grid, temp): if x == 0 and y == 0: return grid[x][y] elif x == 0: if temp[x][y-1] == -1: temp[x][y] = self.pro_recur(x, y-1, grid, temp) + grid[x][y] else: temp[x][y] = temp[x][y-1] + grid[x][y] return temp[x][y] elif y == 0: if temp[x-1][y] == -1: temp[x][y] = self.pro_recur(x-1, y, grid, temp) + grid[x][y] else: temp[x][y] = temp[x-1][y] + grid[x][y] return temp[x][y] else: if temp[x-1][y] == -1 and temp[x][y-1] == -1: temp[x][y] = min(self.pro_recur(x, y-1, grid, temp), self.pro_recur(x-1, y, grid, temp)) + grid[x][y] elif temp[x-1][y] != -1: temp[x][y] = min(self.pro_recur(x, y-1, grid, temp), temp[x-1][y]) + grid[x][y] elif temp[x][y-1] != -1: temp[x][y] = min(self.pro_recur(x-1, y, grid, temp), temp[x][y-1]) + grid[x][y] else: temp[x][y] = min(temp[x-1][y], temp[x][y-1]) + grid[x][y] return temp[x][y]动态规划方法,时间复杂度为
,空间复杂度为
:
class Solution(object): def minPathSum(self, grid): """ :type grid: List[List[int]] :rtype: int """ row, column = len(grid), len(grid[0]) dp = [[0 for i in range(column)] for j in range(row)] dp[0][0] = grid[0][0] for i in range(1, column): dp[0][i] = dp[0][i-1] + grid[0][i] for i in range(1, row): dp[i][0] = dp[i-1][0] + grid[i][0] for i in range(1, row): for j in range(1, column): dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j] return dp[-1][-1]压缩的动态规划方法,时间复杂度为
,空间复杂度为
:
class Solution(object): def minPathSum(self, grid): """ :type grid: List[List[int]] :rtype: int """ row, column = len(grid), len(grid[0]) dp = [0 for i in range(column)] dp[0] = grid[0][0] for i in range(1, column): dp[i] = grid[0][i] + dp[i-1] for i in range(1, row): dp[0] += grid[i][0] for j in range(1, column): dp[j] = min(dp[j-1], dp[j]) + grid[i][j] return dp[-1]3. 换钱最少货币数
给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个aim,代表要找的钱数,求组成aim的最少货币数。

该题的递归方程:,其中
代表数组
组成
的最少货币数,其中
,
,
```python def minCoins(L, aim): dp = [[float(‘inf’) for i in range(aim+1)] for j in range(len(L))] for i in range(aim+1):
if i % L[0] == 0: dp[0][i] = i // L[0]for i in range(1, len(L)):
for j in range(0, aim+1): k = j // L[i] if k == 0: dp[i][j] = dp[i-1][j] else: total_min = float('inf') for p in range(k): local = dp[i-1][j-p*L[i]] + p total_min = local if total_min > local else total_min dp[i][j] = total_minif dp[-1][-1] == float(‘inf’):
return -1else:
return dp[-1][-1]
import sys
lenL, aim = sys.stdin.readline().split()
aim = int(aim)
str_L = sys.stdin.readline().split()
num_L = []
for in strL:
num_L.append(int())
res = minCoins(num_L, aim)
print(res)
```
时间复杂度,空间复杂度

