Haar小波变换的原理及其实现

关键词：Haar, Wavlet

Haar小波的基本原理

梳理自

• https://zhuanlan.zhihu.com/p/63190508
• http://www.360doc.com/content/13/0925/12/10724725_316957631.shtml

  一维

  Haar小波在一维上要做两件事：
  （相邻两个数）求均值（求均值本质上是求和）和求差值
  用均值表示图像的整体信息，用差值表示图像的细节信息

如数组：[2,4,6,8,10,12,14,16]
求均值（整体信息）：[3,7,11,15]； 求差值（细节信息）：[-1,-1,-1,-1] —> 因此，Harr小波分解后，尺寸会变成原来的一半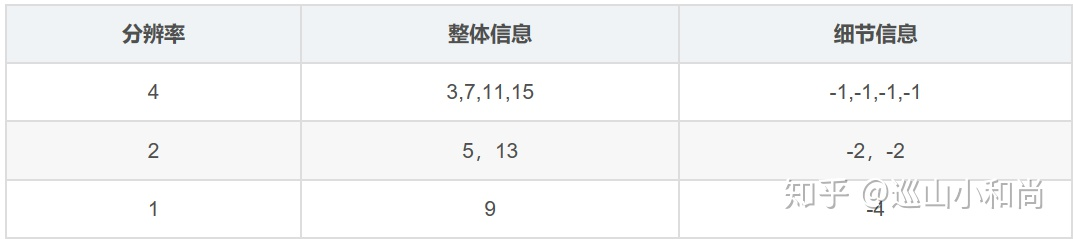

二维

对于二维haar小波，（1）首先，沿着矩阵的每一行做一维的Haar变换；（2）然后，沿着矩阵的每一列做一维的哈尔变换；（3）对于每个低频分量矩阵（近似信息）重复步骤（1）和（2）直到完成指定的等级划分。过程如下：

图中的低频和高频就对应着一维中的整体和细节
行分解和列分解的顺序是可以互换的，保持一致即可。

Haar小波实现

我是基于Deep Learning做图像生成的，推荐一个库pytorch_wavlet。
https://pytorch-wavelets.readthedocs.io/en/latest/readme.html
https://github.com/fbcotter/pytorch_wavelets

自带的example如下：

import torch
from pytorch_wavelets import DWTForward, DWTInverse # (or import DWT, IDWT)
xfm = DWTForward(J=3, mode='zero', wave='db3')  # Accepts all wave types available to PyWavelets
ifm = DWTInverse(mode='zero', wave='db3')
X = torch.randn(10,5,64,64)
Yl, Yh = xfm(X)
print(Yl.shape)
>>> torch.Size([10, 5, 12, 12])
print(Yh[0].shape)
>>> torch.Size([10, 5, 3, 34, 34])
print(Yh[1].shape)
>>> torch.Size([10, 5, 3, 19, 19])
print(Yh[2].shape)
>>> torch.Size([10, 5, 3, 12, 12])
Y = ifm((Yl, Yh))
import numpy as np
np.testing.assert_array_almost_equal(Y.cpu().numpy(), X.cpu().numpy())

我使用的过程中，（1）会先做小波分解，把一个尺寸的图像拼接起来，变成pytorch的[batch_size, channel, H, W]形式；（2）处理完毕后，将各个尺寸的分频结果再做小波逆变换合成原尺寸图像

因此，我会将每张个尺寸的图像保存成字典，使用方法如下：

    # 分解过程
    def get_wavlet(img):
        '''
        我期望得到一个字典，有4个key，分别为stride=8的12通道，stride=4的9通道，stride=2的9通道, 原图
        s8: torch.Size([4, 12, 64, 64])
        s4: torch.Size([4, 9, 128, 128])
        s2: torch.Size([4, 9, 256, 256])
        s1: torch.Size([4, 3, 512, 512])
        '''
        from pytorch_wavelets import DWTForward
        xfm = DWTForward(J=3, mode='zero', wave='haar').cuda()
        Yl, Yh = xfm(img)
        Yh_retensors = {}
        for idx, tmp in enumerate(Yh):
            stride = 2 ** (idx + 1)
            Yh_retensors[f's{stride}'] = tmp.reshape(tmp.shape[0], -1, tmp.shape[3], tmp.shape[4])
        tensors = {}
        tensors['s8'] = torch.cat([Yl, Yh_retensors['s8']], dim=1)
        tensors['s4'] = Yh_retensors['s4']
        tensors['s2'] = Yh_retensors['s2']
        tensors['s1'] = img
        return tensors
    # 还原过程：
    def IDWT(tensors):
        '''
        tensors是个字典，包含stride=8的12通道，stride=4的9通道，stride=2的9通道
        s8: torch.Size([4, 12, 64, 64])
        s4: torch.Size([4, 9, 128, 128])
        s2: torch.Size([4, 9, 256, 256])
        需要将它还原是DWTInverse函数需要的形式，并最终生成原图
        '''
        Yl = tensors['s8'][:, :3]
        Yh = [tensors['s2'], tensors['s4'], tensors['s8'][:, 3:]]
        for idx in range(len(Yh)):
            Yh[idx] = Yh[idx].reshape(Yh[idx].shape[0], 3, -1, Yh[idx].shape[2], Yh[idx].shape[3])
        ifm = DWTInverse(mode='zero', wave='haar').cuda()
        output = ifm((Yl, Yh))
        return output