Normalization太长了，后面都用norm代替

Abstract

归一化对深度神经网络很重要，但每一层用的归一化都是固定的。
Batch-Instance Norm第一批提出在不同层使用不同归一化的策略。但是，使用clip function后（这个地方不理解，要补课。20200508补充：这里的clip和clip gradients一样，设置一个阈值，利用这个阈值调整某一变量的大小），BIN对于0/1输入不可微，，而且合并后的特征图不具备归一化分布，是不利于DCNN训练的。
本文提出了Instance-Layer Normalization（ILN），对于特征图的合并，它使用了Sigmoid方法和级联的Group norm，效果惊人。

Introduction

介绍DCNN和normalization layer
介绍基本概念，特征图的尺寸是(N, H, W, C)，N是batch size，H、W是特征图的高、宽，C是特征图的通道数。

• Batch Normalization（BN），第一个提出的归一化方法，在（N，H，W）上计算均值和方差
• Instance Norm（IN），在（H，W）上计算，以获得更快的风格化
• Layer Norm（LN），在（H，W，C）上计算，为了recurrent network提出（RNN）
• Group Norm（GN），在（H，W）和多通道上计算，在图像分类和实例分割中被证实有效
• Weight Norm（WN），调整权重大小，用于RNN和强化学习
• Batch Kalman Norm考虑了之前所有的方法
• Batch-Instance Norm（BIN），使用一个可训练的参数结合了BN和IN。但是有两个风险：1）可训练的参数被Clip function限制在[0,1]；2）被合并的特征图不在是归一化的分布，对于DCNN的训练十分不利。
• Instance-Layer Norm（ILN），本文的方法有两大亮点。1）使用sigmoid解决0/1输入时clip的不可微问题；2）合并特征图后，使用了一组额外的GN16-GN操作，保证其归一化分布。

U-Net是一个被广泛使用的网络，本文用它在数据集RV和LV图像分割任务中验证ILN的作用。DSC（Dice Similarity Coefficient）结果表明ILN的准确率远超现有的归一化方法。

Methodology

Instance-Layer Norm

IN

首先介绍IN。假设特征图F的尺寸是(N, H, W, C)，IN的计算均值和方差的方法是：


计算输出特征图：
把这个公式记为公式2。下文老是用到这个公式。

LN

对于同样的特征图F，LN计算均值和方差的方式如下：


和IN一样的方式计算输出特征图

结合IN和LN

下文用F_I表示IN的输出结果，F_L表示LN的输出结果。本文使用了一个可学习的参数ρ来合并F_I和F_L。BIN中，ρ被使用了clip方法限制在[0,1]范围中，如下图所示。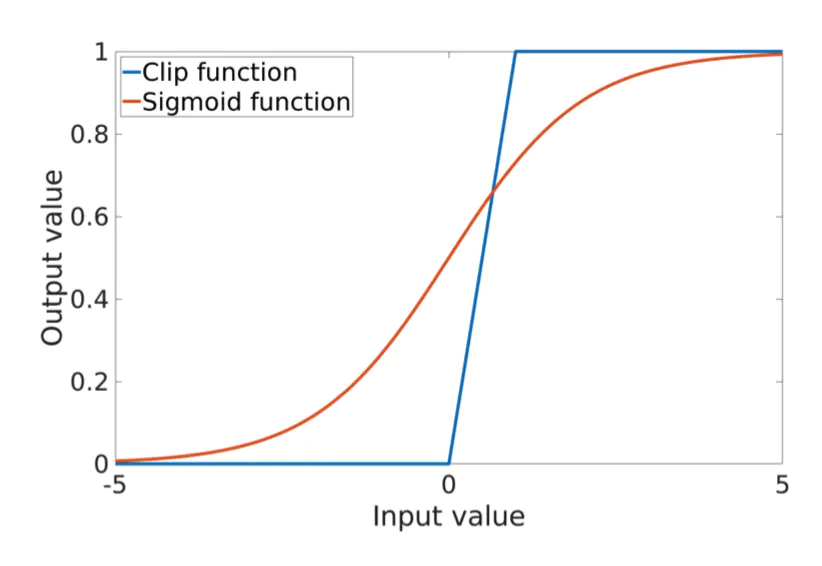

image.png
clip方法在0和1处是不可微的。因此本文中，作者使用signoid方法来解决这一潜在问题。


另一个BIN潜在的问题是合并结果不再符合均值为0，方差为1的分布。本文在F_IL基本上使用额外的GN16操作。


这里M是每个group的通道数。// 是整数除法, g的范围是[1,16]（代表第几组）。这边的公式之前没接触过，乍一看还不理解，后来理了下，就是基础的Group Norm，分成了约16个组。利用公式2得到F_ILN后，依照BN的做法，用可学习参数α和β来保持DCNN的特征表达能力：

Experimental Setup

Network Architecture

医学图像分割普遍采用的网络结构是U-Net，初始特征通道数是16.norm layer加在conv和relu层之间。
损失函数用交叉熵。
优化函数用的Stochastic Gradient Descent（SGD），Momentum设置为0.9
权重使用截断的正态分布，标准差为2/（3^2*C)，C为通道数
偏差初始化为0.1
ρ被初始化为0.5

Data Collections

图像尺寸 256*256，包含6082RV图和805LV图，对图像做了三个角度的旋转（不同数据集的旋转角度不一样）

Implementation

为了公平，对其它归一化方法用了非高度集成的tensorflow来实现

Experiments

评价标准是DSC，每个实验训练2个epoch，学习率第二次时会除以5。学习率被初始化成（1.5, 1.0, 0.5, 0.1, 0.05)，选择了效果最佳的学习率。

Code

我现在用的ILN和论文里介绍的有一定差别，学习一下写法。
pytorch的特征图尺寸为(batch_size, channels, height, width)

import torch.nn as nn
import torch.nn.parameter as Parameter
class ILN(nn.Module):
    def __init__(self, num_features, eps=1e-5):
        super(ILN, self).__init__()
        self.eps = eps
        self.rho = Parameter(torch.Tensor(1, num_features, 1, 1))
        self.gamma = Parameter(torch.Tensor(1, num_features, 1, 1))
        self.beta = Parameter(torch.Tensor(1, num_features, 1, 1))
        self.rho.data.fill_(0.0) # 初始化的方法和论文中不太一样
        self.gamma.data.fill_(1.0)
        self.beta.data.fill_(0.0)
    def forward(self, x):
        in_mean = torch.mean(x, dim=[2,3], keepdim=True) # dim=[2,3]表示对H*W算均值，方差同理
        in_var = torch.var(x, dim=[2,3], keepdim=True, unbiased=False)
        out_in = (x - in_mean) / torch.sqrt(in_var + self.eps) # 计算IN的输出
        ln_mean = torch.mean(x, dim=[1,2,3], keepdim=True) # dim=[1,2,3]表示对C*H*W算均值，方差同理
        ln_var = torch.var(x, dim=[1,2,3], keepdim=True, unbiased=False)
        out_ln = (x - ln_mean) / torch.sqrt(ln_var + self.eps) # 计算LN的输出
        self.rho.ata = self.rhodata.clamp(0.0, 1.0) #这儿的clamp就是clip，没有用到Sigmoid
        out = self.rho.expand(x.shape[0], -1, -1, -1) * out_in + (1-self.rho.expand(x.shape[0], -1, -1, -1)) * out_ln # 加权求和
        out = out * self.gamma.expand(x.shape[0], -1, -1, -1) + self.beta.expand(x.shape[0], -1, -1, -1) #依照BN进行放缩
        return out