不同的算法时间复杂度

原文： https://javatutorial.net/algorithm-time-complexities

在开始解释不同的时间复杂度之前，让我们首先看一下实际的算法是什么。

算法的正式定义是“在计算或其他解决问题的操作（尤其是计算机）中要遵循的过程或规则集”。 因此，换句话说，算法是定义的路径，例如计算机使用该算法来完成给定问题的解决方案。

算法工作流程

尽管听起来很简单且不复杂，但事实恰恰相反。 许多算法要花费大量时间才能完成某件事，而有些则没有。 这就是为什么了解给定算法的复杂度非常重要的原因。 那是因为通过了解算法的复杂度，可以使我们了解算法的“价值”，或者说效率如何。

算法示例：

• 图片搜寻
• 语音输入
• 意见建议
• 谷歌地图
• 谷歌新闻
• 等等

具有讽刺意味的算法示例

不同类型的算法复杂度

• 恒定时间：O(1)

如果时间量不取决于输入大小，则可以说算法大小以恒定时间运行。

一个例子是从数组访问元素。 您只需“调用”数组的索引即可访问数组的元素。

• 线性时间：O(n)

线性时间是指算法取决于的输入大小。 如果输入大小为 n ，则复杂度也将为 n。

具有这种时间复杂度的算法的一个著名示例是线性搜索。

• 对数时间：O(log n)

如果执行时间与输入大小的对数成正比，则可以说该算法以对数时间运行。

这种时间复杂度的算法的一个著名示例是二分搜索。

• 二次时间：O(n^2)

二次时间是指执行时间为输入大小的平方。

例如冒泡排序，选择排序，插入排序。

• “大 Ω”的定义

大欧米茄，也称为下界，用Ω符号表示。

大 O

如果执行时间与输入大小的对数成正比，则可以说该算法以对数时间运行。 例如，如果 Java 中有一个数组，其中包含 5 个苹果，并且您需要打印每个苹果，则该数组将为O(5)或换句话说，为O(数组长度)或O(n)。

这种时间复杂度的算法的一个著名示例是二分搜索。

大 Θ

如果T(n)是Θ(f(n))，则意味着T(n)增长（精确）与f(n)一样快。n + n仍然是 n。 是不是有点满嘴？ 让我们尝试一个更简单的解释。

您可以将大 Θ 视为：

“花费的时间不会超过且不短于”

如何确定给定程序的复杂度

int sumArray(int[] aiNumbers)
{
   int iSum = 0;
   for (int i=0; i<aiNumbers.length; i++)
      iSum += aiNumbers[i];
   return iSum;
}

该程序的复杂度只是aiNumbers.length。 因此，如果此数组的长度为 4，则复杂度为 4。如果aiNumbers.length为 6，则复杂度为 6。

复杂度是aiNumbers.length的原因是因为它会循环aiNumbers.length次。 因此，复杂度为O(N)。

N = in.length;
i = 0;
while (i < N) { 
   for (int i=N-2; i<N; i++) {
      System.out.println("Do something.");
   }
}

上面程序的复杂度为N * N，即 N 乘以 2 的幂。这是因为for循环每次将运行 N 次，而整个循环将运行 N 次。 因此，N *N。因此，该算法的复杂度是二次（O(n^2)）

for (int i = 0; i < n; i++) {
   // do something
}
for (int i = 0; i < n; i++) {
   // do something
}

在上面的示例中，算法的时间复杂度为 n 。 这样做的原因是因为有 2 个循环 n 次循环 – n + n。 简而言之，n + n就是 n 。

每种算法的可视化表示

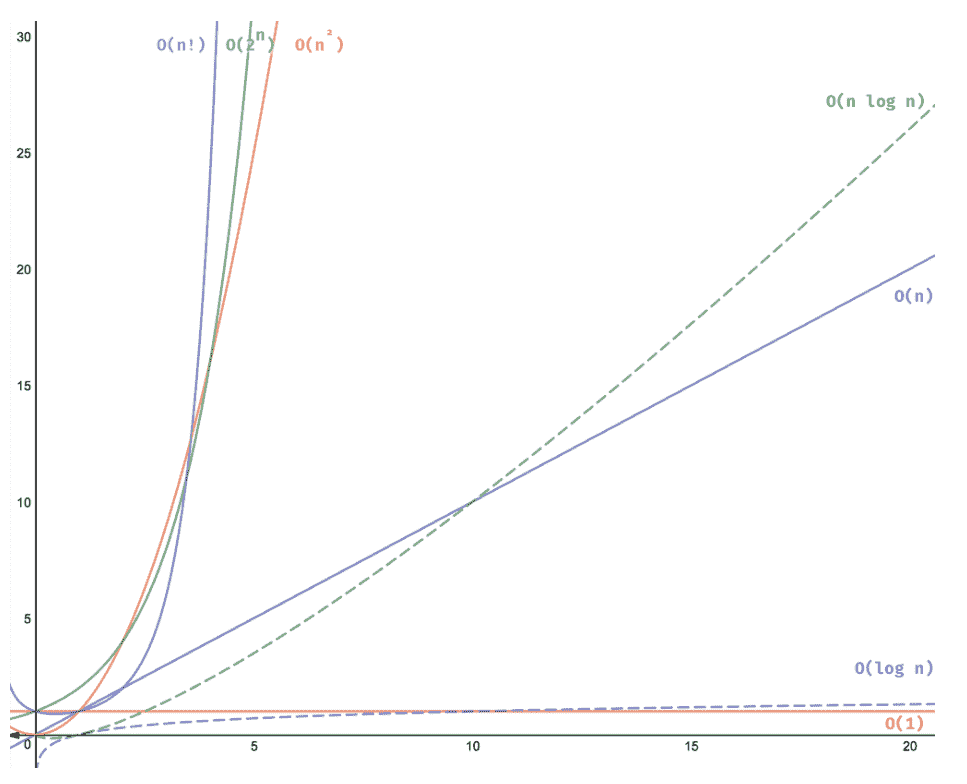
视觉表示

图片来源： https://adrianmejia.com/most-popular-algorithms-time-complexity-every-programmer-should-know-free-online-tutorial-course/

在算法和复杂度方面，请尽可能尝试优化算法。 这样做的一个好方法是使用集合等在输入数据中找到共同点。请记住：内存很昂贵，您的时间也很昂贵。