以一定的顺序规则，逐个访问二叉树的所有结点，这个过程就是二叉树的遍历。按照顺序规则的不同，遍历方式有以下四种：

  • 先序遍历
  • 中序遍历
  • 后序遍历
  • 层次遍历

按照实现方式的不同，遍历方式又可以分为以下两种：

  • 递归遍历（先、中、后序遍历）
  • 迭代遍历（层次遍历）

遍历的三种顺序

  • 根结点 -> 左子树 -> 右子树
  • 左子树 -> 根结点 -> 右子树
  • 左子树 -> 右子树 -> 根结点

上述三个遍历顺序，就分别对应了二叉树的先序遍历、中序遍历和后序遍历规则。

在这三种顺序中，根结点的遍历分别被安排在了首要位置、中间位置和最后位置。
所谓的“先序”、“中序”和“后序”，“先”、“中”、“后”其实就是指根结点的遍历时机。

先序遍历

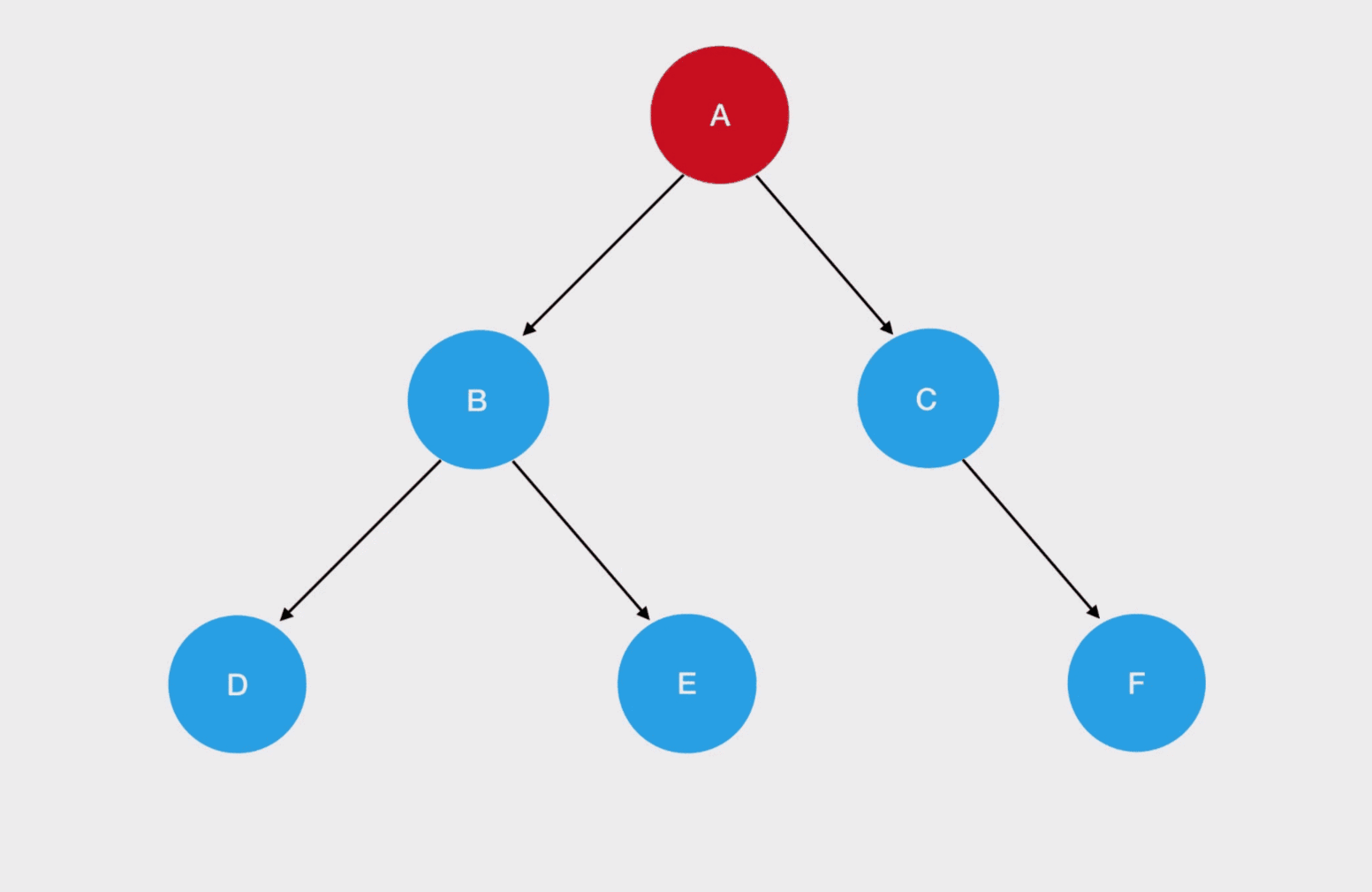
image.png
上面图中二叉树的结构用代码来表示：

  1. const root = {
  2.   val: "A",
  3.   left: {
  4.     val: "B",
  5.     left: {
  6.       val: "D"
  7.     },
  8.     right: {
  9.       val: "E"
  10.     }
  11.   },
  12.   right: {
  13.     val: "C",
  14.     right: {
  15.       val: "F"
  16.     }
  17.   }
  18. };

递归函数的编写要点

编写一个递归函数之前，首先要先明确两个东西：

  • 递归式
  • 递归边界

递归式，它指的是你每一次重复的内容是什么。在这里，我们要做先序遍历，那么每一次重复的其实就是 根结点 -> 左子树 -> 右子树 这个旅行路线。
递归边界，它指的是你什么时候停下来。
在遍历的场景下，当我们发现遍历的目标树为空的时候，就意味着旅途已达终点、需要画上句号了。这个“画句号”的方式，在编码实现里对应着一个 return 语句——这就是二叉树遍历的递归边界。

先序遍历的编码实现：

  1. // 所有遍历函数的入参都是树的根结点对象
  2. function preorder(root) {
  3.     // 递归边界，root 为空
  4.     if(!root) {
  5.         return 
  6.     }
  8.     // 输出当前遍历的结点值
  9.     console.log('当前遍历的结点值是：', root.val)  
  10.     // 递归遍历左子树 
  11.     preorder(root.left)  
  12.     // 递归遍历右子树  
  13.     preorder(root.right)
  14. }

中序遍历

递归边界照旧，唯一发生改变的是递归式里调用递归函数的顺序——左子树的访问会优先于根结点。我们参考先序遍历的分析思路，来写中序遍历的代码：

  1. // 所有遍历函数的入参都是树的根结点对象
  2. function inorder(root) {
  3.     // 递归边界，root 为空
  4.     if(!root) {
  5.         return 
  6.     }
  8.     // 递归遍历左子树 
  9.     inorder(root.left)  
  10.     // 输出当前遍历的结点值
  11.     console.log('当前遍历的结点值是：', root.val)  
  12.     // 递归遍历右子树  
  13.     inorder(root.right)
  14. }

后序遍历

在后序遍历中，我们先访问左子树，再访问右子树，最后访问根结点：

  1. function postorder(root) {
  2.     // 递归边界，root 为空
  3.     if(!root) {
  4.         return 
  5.     }
  7.     // 递归遍历左子树 
  8.     postorder(root.left)  
  9.     // 递归遍历右子树  
  10.     postorder(root.right)
  11.     // 输出当前遍历的结点值
  12.     console.log('当前遍历的结点值是：', root.val)  
  13. }