输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

  1. 3

/ \ 9 20 / \ 15 7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

  1.    1
  2.   / \
  3.  2   2
  4. / \

3 3 / \ 4 4

返回 false 。

思路：从上往下遍历树中的每一个结点，计算其左右子树的高度并进行对比，只要有一个高度差的绝对值大于 1，那么整棵树都会被判为不平衡

  1. const isBalanced = function(root) {
  2.   // 立一个flag，只要有一个高度差绝对值大于1，这个flag就会被置为false
  3.   let flag = true
  4.   // 定义递归逻辑
  5.   function dfs(root) {
  6.       // 如果是空树，高度记为0；如果flag已经false了，那么就没必要往下走了，直接return
  7.       if(!root || !flag) {
  8.           return 0 
  9.       }
  10.       // 计算左子树的高度
  11.       const left = dfs(root.left)  
  12.       // 计算右子树的高度
  13.       const right = dfs(root.right)  
  14.       // 如果左右子树的高度差绝对值大于1，flag就破功了
  15.       if(Math.abs(left-right) > 1) {
  16.           flag = false
  17.           // 后面再发生什么已经不重要了，返回一个不影响回溯计算的值
  18.           return 0
  19.       }
  20.       // 返回当前子树的高度
  21.       return Math.max(left, right) + 1
  22.   }
  24.   // 递归入口
  25.   dfs(root) 
  26.   // 返回flag的值
  27.   return flag
  28. };

平衡二叉树的构造

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。
如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。
如果有多种构造方法，请你返回任意一种。

示例：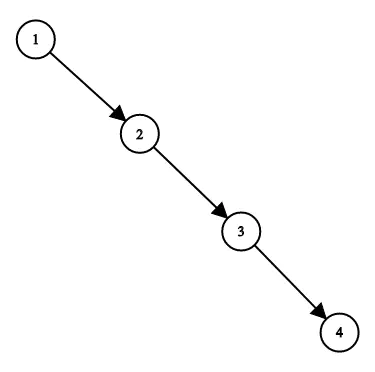
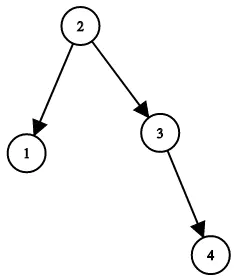
image.png
image.png

输入：root = [1,null,2,null,3,null,4,null,null] 输出：[2,1,3,null,null,null,4] 解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

提示： 树节点的数目在 1 到 10^4 之间。 树节点的值互不相同，且在 1 到 10^5 之间。

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {TreeNode}
  4.  */
  5. const balanceBST = function(root) {
  6.     // 初始化中序遍历序列数组
  7.     const nums = []
  8.     // 定义中序遍历二叉树，得到有序数组
  9.     function inorder(root) {
  10.         if(!root) {
  11.             return 
  12.         }
  13.         inorder(root.left)  
  14.         nums.push(root.val)  
  15.         inorder(root.right)
  16.     }
  18.     // 这坨代码的逻辑和上一节最后一题的代码一模一样
  19.     function buildAVL(low, high) {
  20.         // 若 low > high，则越界，说明当前索引范围对应的子树已经构建完毕
  21.         if(low>high) {
  22.             return null
  23.         }
  24.         // 取数组的中间值作为根结点值
  25.         const mid = Math.floor(low + (high -low)/2)
  26.         // 创造当前树的根结点
  27.         const cur = new TreeNode(nums[mid])  
  28.         // 构建左子树
  29.         cur.left = buildAVL(low, mid-1) 
  30.         // 构建右子树
  31.         cur.right = buildAVL(mid+1, high)  
  32.         // 返回当前树的根结点 
  33.         return cur
  34.     }
  35.     // 调用中序遍历方法，求出 nums
  36.     inorder(root)
  37.     // 基于 nums，构造平衡二叉树
  38.     return buildAVL(0, nums.length-1)
  39. };