深度优先搜索的核心思想，是试图穷举所有的完整路径。

深度优先搜索的本质——栈结构

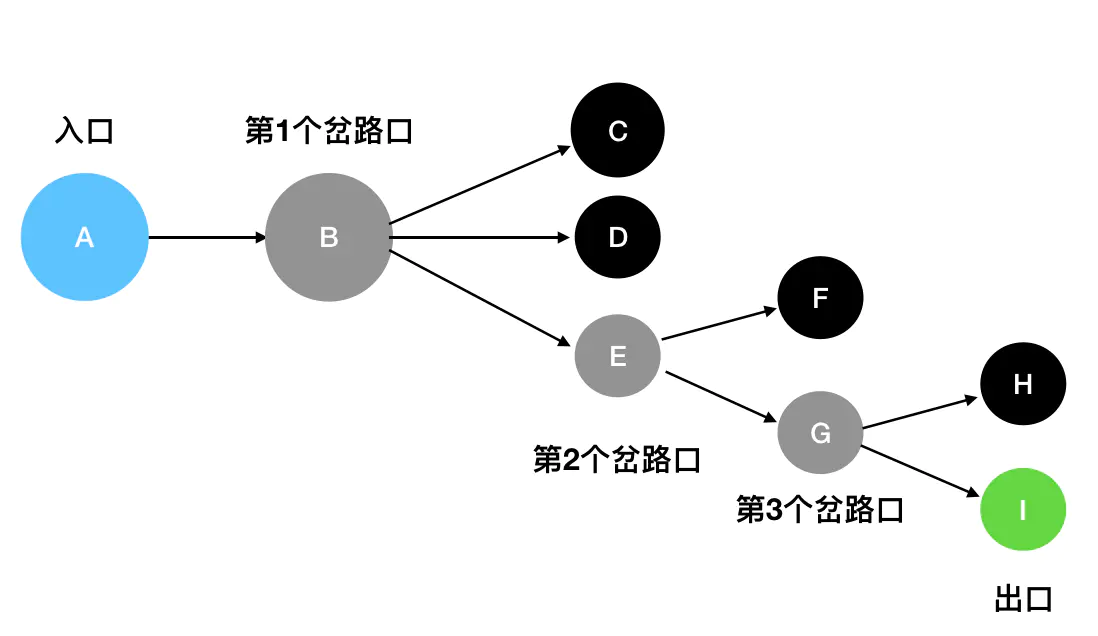
image.png
想向我们在玩一个迷宫游戏，入口是 A，出口是 I。
灰色的是岔路口，黑色的是死胡同，绿色的是出口。

基于眼前的这个迷宫结构，我们来一步一步模拟一下深度优先搜索的具体过程：

  1. 从 A 出发，沿着唯一的一条道路往下走，遇到了第1个岔路口B。眼前有三个选择：C、D、E。这里我按照从上到下的顺序来走（你也可以按照其它顺序），先走C。
  2. 发现 C是死胡同，后退到最近的岔路口 B，尝试往D方向走。
  3. 发现D 是死胡同，，后退到最近的岔路口 B，尝试往E方向走。
  4. E 是一个岔路口，眼前有两个选择：F 和 G。按照从上到下的顺序来走，先走F。
  5. 发现F 是死胡同，后退到最近的岔路口 E，尝试往G方向走。
  6. G 是一个岔路口，眼前有两个选择：H 和 I。按照从上到下的顺序来走，先走H。
  7. 发现 H 是死胡同，后退到最近的岔路口 G，尝试往I方向走。
  8. I 就是出口，成功走出迷宫。

观察这个过程，我们发现这些前进、后退的操作，其实和栈结构的入栈、出栈过程非常相似

现在我们把迷宫中的每一个坐标看做是栈里面的一个元素，用栈来模拟这个过程：

  1. 从 A 出发（A入栈），经过了B（B入栈），接下来面临 C、D、E三条路。这里按照从上到下的顺序来走（你也可以选择其它顺序），先走C（C入栈）。
  2. 发现 C是死胡同，后退到最近的岔路口 B（C出栈），尝试往D方向走（D入栈）。
  3. 发现D 是死胡同，，后退到最近的岔路口 B（D出栈），尝试往E方向走（E入栈）。
  4. E 是一个岔路口，眼前有两个选择：F 和 G。按照从上到下的顺序来走，先走F（F入栈）。
  5. 发现F 是死胡同，后退到最近的岔路口 E（F出栈），尝试往G方向走（G入栈）。
  6. G 是一个岔路口，眼前有两个选择：H 和 I。按照从上到下的顺序来走，先走H（H入栈）。
  7. 发现 H 是死胡同，后退到最近的岔路口 G（H出栈），尝试往I方向走（I入栈）。
  8. I 就是出口，成功走出迷宫。

此时栈里面的内容就是A、B、E、G、I，因此 A->B->E->G->I 就是走出迷宫的路径。通过深度优先搜索，我们不仅可以定位到迷宫的出口，还可以记录下相关的路径信息。

DFS 中，我们往往使用递归来模拟入栈、出栈逻辑。

DFS 与二叉树遍历

现在我们站在深度优先搜索的角度，重新理解一下二叉树的先序遍历过程：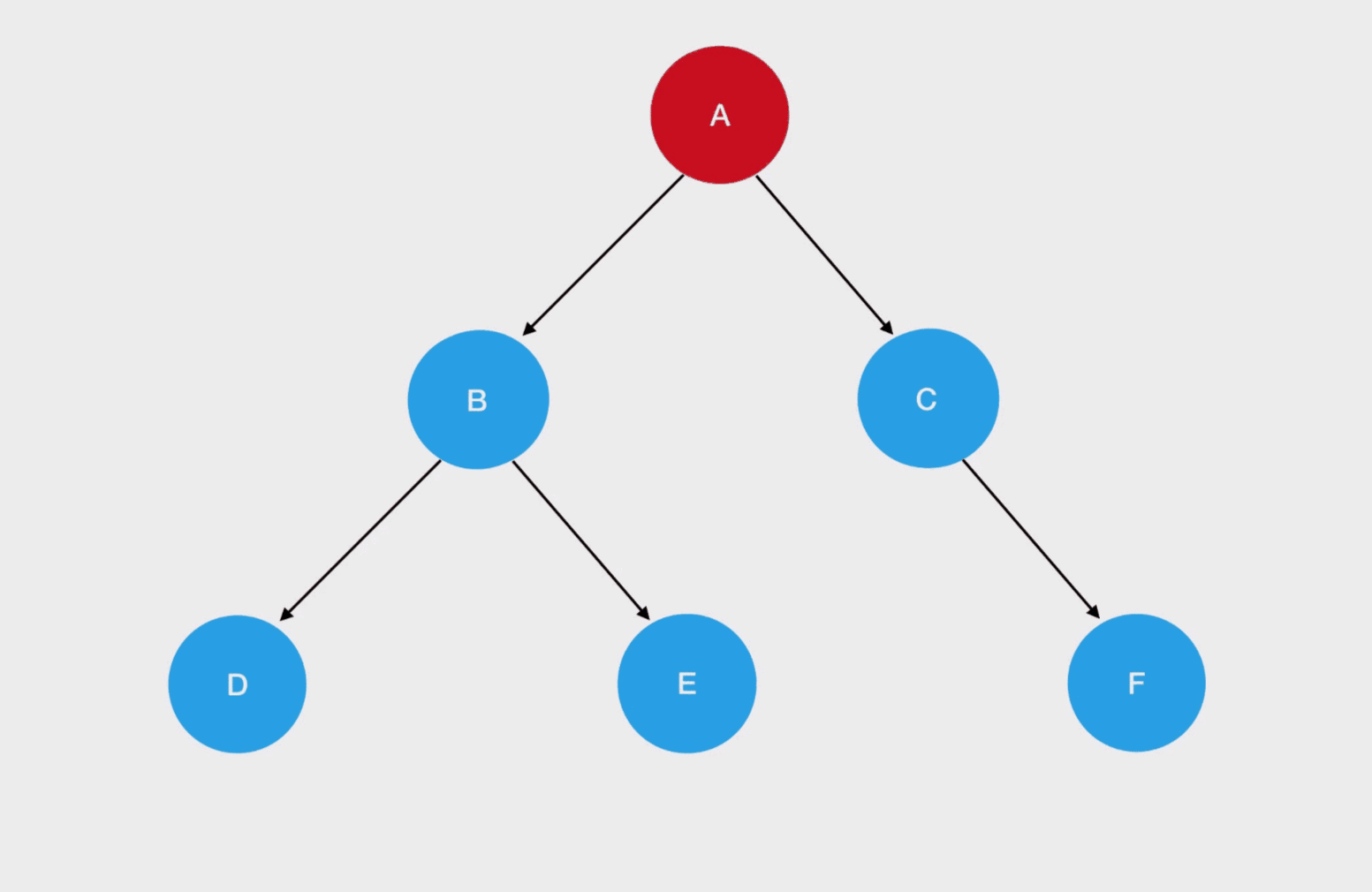
image.png
从 A 节点出发，访问左侧的子节点；如果左子树同样存在左侧子节点，就头也不回继续访问下去。一直到左侧子节点为空时，才退回到距离最近的父节点、再尝试去访问父节点的右侧子节点——这个过程，和走迷宫是何其相似！
在二叉树中，节点就好比是迷宫中的坐标，图中的每个节点在作为父节点时无疑是岔路口，而空节点就是死胡同。

  1. // 所有遍历函数的入参都是树的根结点对象
  2. function preorder(root) {
  3.     // 递归边界，root 为空
  4.     if(!root) {
  5.         return 
  6.     }
  8.     // 输出当前遍历的结点值
  9.     console.log('当前遍历的结点值是：', root.val)  
  10.     // 递归遍历左子树 
  11.     preorder(root.left)  
  12.     // 递归遍历右子树  
  13.     preorder(root.right)
  14. }

在这个递归函数中，递归式用来先后遍历左子树、右子树（分别探索不同的道路），递归递归边界在识别到空节点的时候回直接返回（死胡同）。因此，我们可以认为，递归式就是我们选择道路的过程，而递归边界就是死胡同。二叉树的先序遍历正是深度优先搜索思想的递归实现。可以说深度优先搜索过程就类似于数的先序遍历、是树的先序遍历的推广。

这时候，可能有同学会有疑问：在二叉树遍历的递归实现里，完全没有栈的影子——这东西似乎和栈没有什么直接联系啊，为啥咱们还说深度优先搜索的本质是栈呢？
我们从两个角度来理解这个事情：

  • 首先，函数调用的底层，仍然是由栈来实现的。JS 会维护一个叫“函数调用栈”的东西，preorder每调用一次自己，相关调用的上下文就会被push进函数调用栈中；待函数执行完毕后，对应的上下文又会从调用栈中被pop出来。因此，即便二叉树的递归调用过程中，并没有出现栈这种数据结构，也依然改变不了递归的本质是栈的事实。
  • 其次，DFS 作为一种思想，它和树的递归遍历一脉相承、却并不能完全地画上等号——DFS 的解题场景其实有很多，其中有一类会要求我们记录每一层递归式里路径的状态，此时就会强依赖栈结构。

广度优先搜索思想（BFS）

与深度优先搜索不同的是，广度优先搜索（BFS）并不执着于“一往无前”这件事情。它关心的是眼下自己能够直接到达的所有坐标，其动作有点类似于“扫描”——比如说站在 B 这个岔路口，它会只关注 C、D、E 三个坐标，至于 F、G、H、I这些遥远的坐标，现在不在它的关心范围内：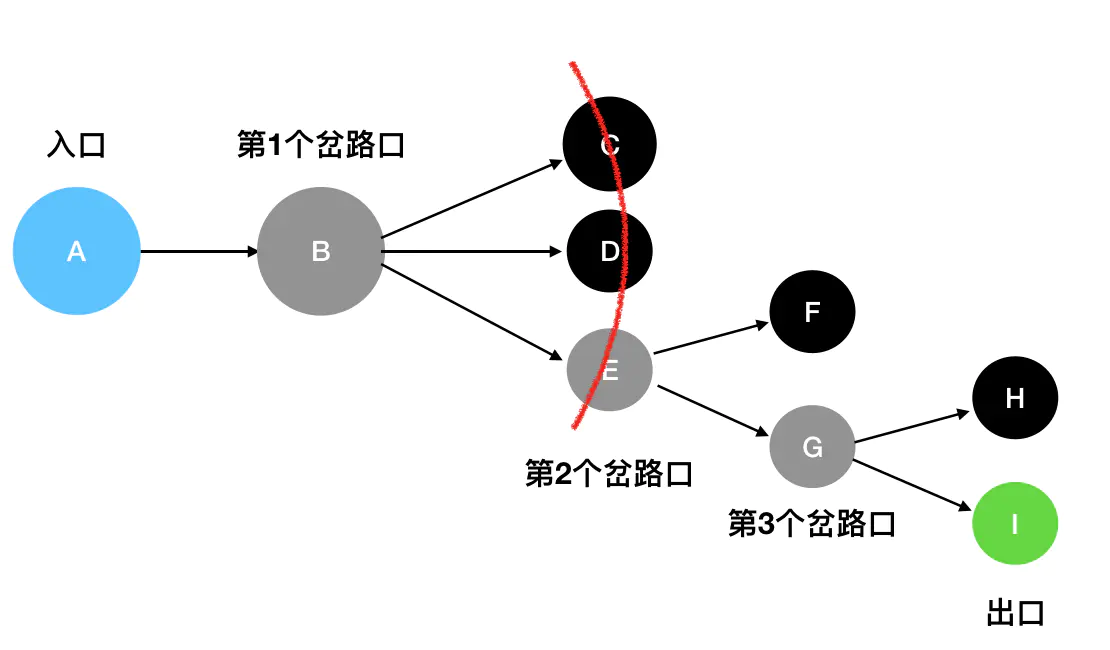
image.png
只有在走到了 E处时，它发现此时可以触达的坐标变成了 F、G，此时才会去扫描F、G：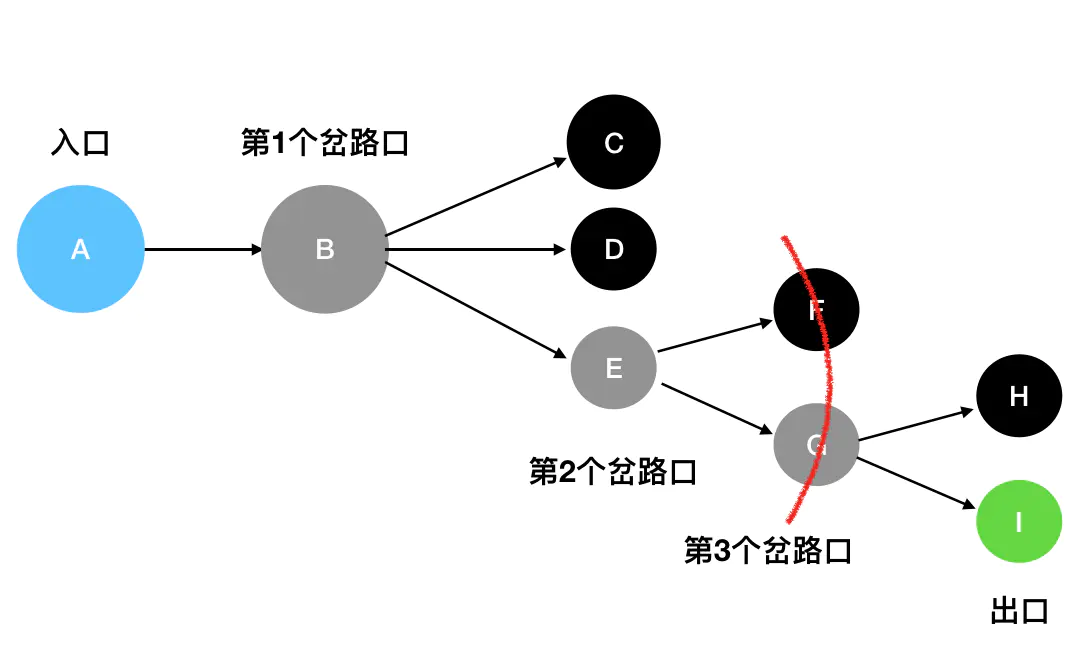
image.png
按照这个思路，广度优先搜索每次以“广度”为第一要务、雨露均沾，一层一层地扫描，最后也能够将所有的坐标扫描完全：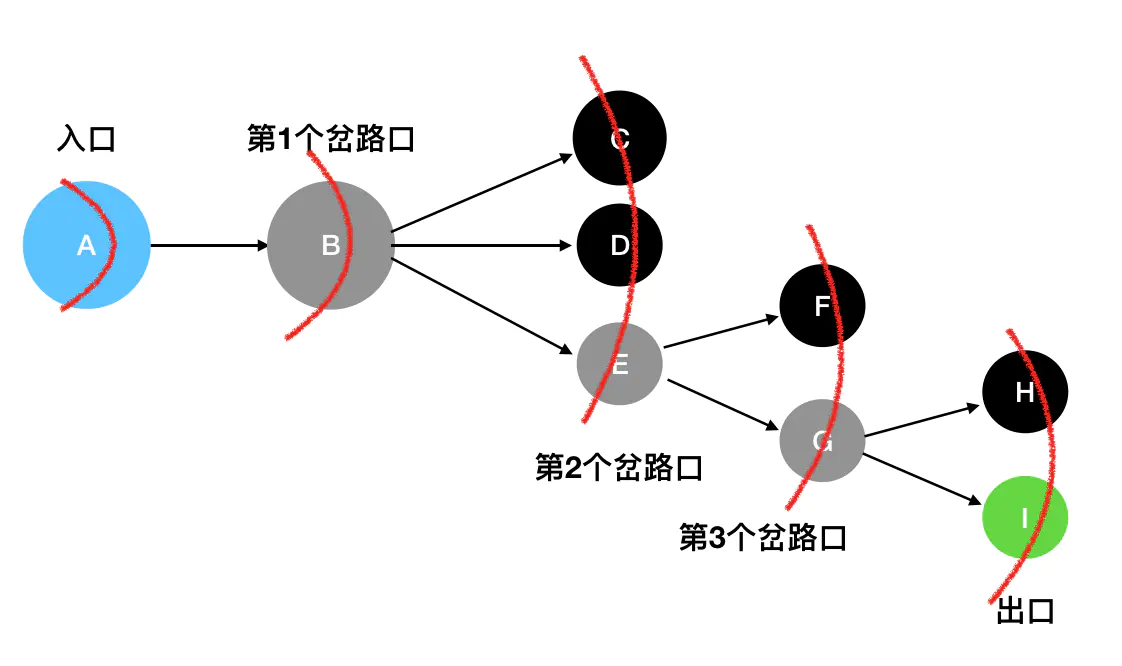
image.png
当扫描到 I 的时候，发现 I 是出口，照样能够找到答案。

按照 BFS 的遍历规则，具体的访问步骤会变成下面这样:

  1. 站在入口A处（第一层），发现直接能抵达的坐标只有B，于是接下来需要访问的就是 B。
  2. 入口A访问完毕，走到 B 处（第二层），发现直接能抵达的坐标变成了C、D和E，于是把这三个坐标记为下一层的访问对象。
  3. B访问完毕，访问第三层。这里我按照从上到下的顺序（你也可以按照其它顺序），先访问 C和D，然后访问E。站在C处和D处都没有见到新的可以直接抵达的坐标，所以不做额外的动作。但是在E处见到了可以直接抵达的F和G，因此把F和G记为下一层（第四层）需要访问的对象。
  4. 第三层访问完毕，访问第四层。第四层按照从上到下的顺序，先访问的是 F。从F出发没有可以直接触达的坐标，因此不做额外的操作。接着访问G，发现从G出发可以直接抵达H和I，因此把H和I记为下一层（第五层）需要访问的对象。
  5. 第四层访问完毕，访问第五层。第五层按照从上到下的顺序，先访问的是H，发现从H出发没有可以直接抵达的坐标，因此不作额外的操作。接着访问I，发现I就是出口，问题得解。

在分层遍历的过程中，大家会发现两个规律：

  1. 每访问完毕一个坐标，这个坐标在后续的遍历中都不会再被用到了，也就是说它可以被丢弃掉。
  2. 站在某个确定坐标的位置上，我们所观察到的可直接抵达的坐标，是需要被记录下来的，因为后续的遍历还要用到它们。

在这个过程里，我们其实循环往复地做了以下事情：
依次访问队列里已经有的坐标，将其出队；记录从当前坐标出发可直接抵达的所有坐标，将其入队。
以上逻辑用伪代码表述如下：

  1. function BFS(入口坐标) {
  2.     const queue = [] // 初始化队列queue
  3.     // 入口坐标首先入队
  4.     queue.push(入口坐标)
  5.     // 队列不为空，说明没有遍历完全
  6.     while(queue.length) {
  7.         const top = queue[0] // 取出队头元素  
  9.         访问 top // 此处是一些和 top 相关的逻辑，比如记录它对应的信息、检查它的属性等等
  11.         // 注意这里也可以不用 for 循环，视题意而定
  12.         for(检查 top 元素出发能够遍历到的所有元素)  {
  13.             queue.push(top能够直接抵达的元素)
  14.         }
  16.         queue.shift() // 访问完毕。将队头元素出队
  17.     }
  18. }

BFS 实战：二叉树的层序遍历

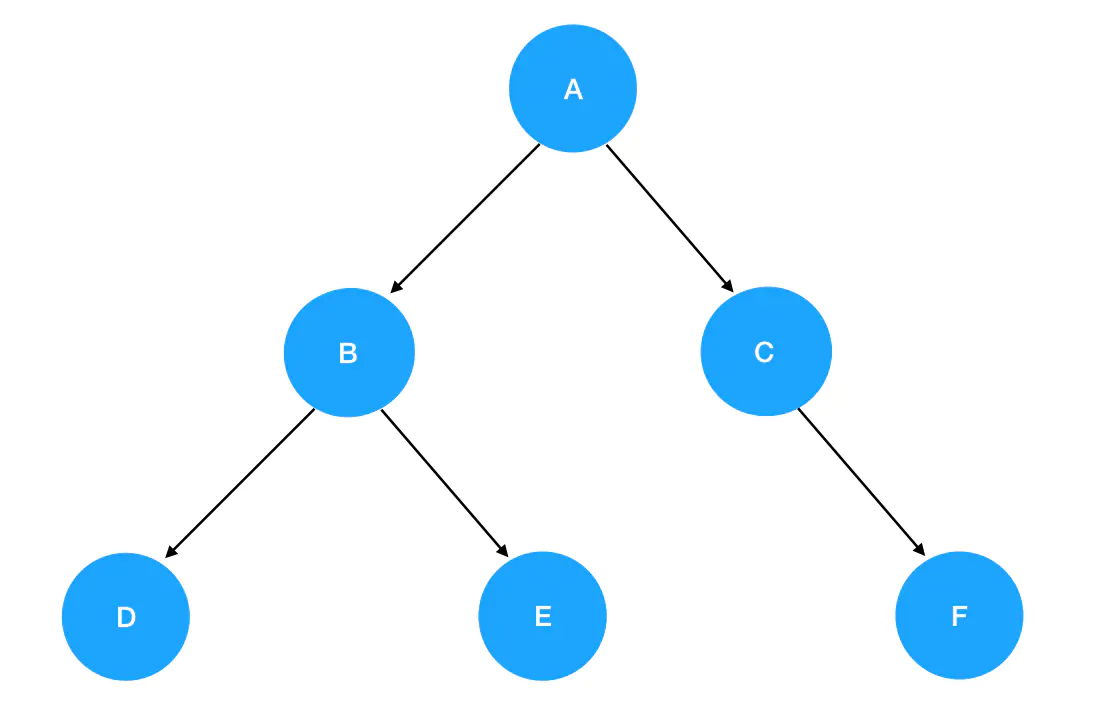
image.png
这棵二叉树的编码实现如下：

  1. const root = {
  2.   val: "A",
  3.   left: {
  4.     val: "B",
  5.     left: {
  6.       val: "D"
  7.     },
  8.     right: {
  9.       val: "E"
  10.     }
  11.   },
  12.   right: {
  13.     val: "C",
  14.     right:{
  15.       val: "F"
  16.     }
  17.   }
  18. }

看到“层次”关键字，大家应该立刻想到“扫描”；想到“扫描”，就应该立刻想到 BFS。因此层序遍历，我们就用 BFS 的思路来实现。这里咱们可以直接套用上面的伪代码：

  1. function BFS(root) {
  2.     const queue = [] // 初始化队列queue
  3.     // 根结点首先入队
  4.     queue.push(root)
  5.     // 队列不为空，说明没有遍历完全
  6.     while(queue.length) {
  7.         const top = queue[0] // 取出队头元素  
  8.         // 访问 top
  9.         console.log(top.val)
  10.         // 如果左子树存在，左子树入队
  11.         if(top.left) {
  12.             queue.push(top.left)
  13.         }
  14.         // 如果右子树存在，右子树入队
  15.         if(top.right) {
  16.             queue.push(top.right)
  17.         }
  18.         queue.shift() // 访问完毕，队头元素出队
  19.     }
  20. }