朴素贝叶斯

买瓜问题**

判断一个西瓜是否成熟：如果我对西瓜没有任何了解，按常理来说，超市里西瓜的的成熟概率是60%。那么，这个概率 P(瓜熟) 就被称为先验概率。先验概率是根据以往经验和分析得到的概率，先验概率无需样本数据，不受任何条件的影响。

突然我知道了一个小知识：瓜熟蒂落。一般来说，瓜蒂脱落的情况下，西瓜成熟的概率大一些，大概是 75%。如果把瓜蒂脱落当作一种结果，然后去推测西瓜成熟的概率，这个概率 P(瓜熟 | 瓜蒂脱落) 就被称为后验概率。后验概率类似于条件概率。

知道了先验概率和后验概率，我们再来看看什么是联合概率。P(瓜熟，瓜蒂脱落) 称之为联合分布，它表示瓜熟了且瓜蒂脱落的概率。关于联合概率，满足下列乘法等式：

P(瓜熟,瓜蒂脱落)=P(瓜熟|瓜蒂脱落)⋅P(瓜蒂脱落)=P(瓜蒂脱落|瓜熟)⋅P(瓜熟)

其中，P(瓜熟 | 瓜蒂脱落) 就是刚刚介绍的后验概率，表示在“瓜蒂脱落”的条件下，“瓜熟”的概率。P(瓜蒂脱落 | 瓜熟) 表示在“瓜熟”的情况下，“瓜蒂脱落”的概率。

接着，如何计算瓜蒂脱落的概率呢？实际上可以分成两种情况：一种是瓜熟状态下瓜蒂脱落的概率，另一种是瓜生状态下瓜蒂脱落的概率。瓜蒂脱落的概率就是这两种情况之和。因此，我们就推导出了全概率公式：

P(瓜蒂脱落)=P(瓜蒂脱落|瓜熟)⋅P(瓜熟)+P(瓜蒂脱落|瓜生)⋅P(瓜生)

单个特征判断瓜熟

好了，介绍完先验概率、后验概率、联合概率、全概率后，我们来看这样一个问题：西瓜的状态分成两种：瓜熟与瓜生，概率分别为 0.6 与 0.4，且瓜熟里面瓜蒂脱落的概率是 0.8，瓜生里面瓜蒂脱落的概率是 0.4。那么，如果我现在挑到了一个瓜蒂脱落的瓜，则该瓜是好瓜的概率多大？

显然，这是一个计算后验概率的问题，根据我们上面推导的联合概率和全概率公式，可以求出：

一项一项来看：
条件概率 P(瓜蒂脱落 | 瓜熟) = 0.8
先验概率 P(瓜熟) = 0.6
条件概率 P(瓜蒂脱落 | 瓜生) = 0.4
先验概率 P(瓜生) = 0.4
将以上数值带入上式，得：

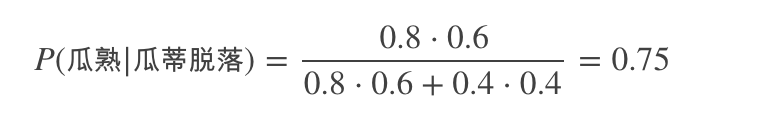
这样，我们就计算得到了瓜蒂脱落的瓜是好瓜的概率是 0.75。注意，以上这种计算后验概率的公式就是利用贝叶斯定理。有点意外吧？不知不觉，可以说你已经掌握了贝叶斯定理的思想了。