2.1 离散型随机变量及分布

两类试验的结果

示数的：降雨量；候车人数；发生交通事故的次数；
非示数的：天气(晴、多云…)；化验结果(阳性、阴性…)

中心问题：将随机试验的结果量化

离散型随机变量

离散型随机变量：随机变量的取值是有限个或可数个
例如：
正奇数集 {1,3,5,7…} 无限但可数，所以是离散型随机变量
掷骰子

概率分布律

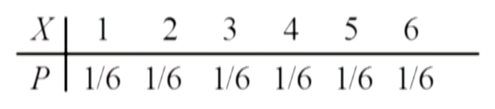
以掷骰子为例，X 是事件，P 是每个事件发生的概率。

常见的几种离散型随机变量：

0-1 分布（两点分布）

事件只有两种取值：0 或 1
比如：

• 产品质量是否合格 合格、不合格
• 登记人员性别 男、女
• 种子是否发芽 是、否

概率分布律为

n 重贝努利试验

试验只有两个结果(0-1 分布)，独立地重复 n 次，叫做 n 重贝努利试验。

假设此人第1门没有通过，则概率是 。这种情况可能会发生在 5 门课程中任意一门，所以需要加上 C。
这里的C公式为： 也可以表示为

二项分布

二项分布是指在只有两个结果的 n 次独立的伯努利试验中，所期望的结果出现次数的概率。
在单次试验中，结果 A 出现的概率为 p，结果 B 出现的概率为 1-p。那么在 n=10，即 10 次试验中，结果 A 出现 0 次、1 次、……、10 次的概率各是多少呢？这样的概率分布呈现出什么特征呢？这就是二项分布所研究的内容。

比如，掷3次硬币，样本空间有 23 = 8 种，每种结果出现的概率为 0.5 = 0.125，正面出现3次、2次、1次、0次的概率分别是0.125、0.375、0.375、0.125。

！需要特别提醒的是：二项分布是建立在有放回抽样的基础上的，也就是抽出一个样品测量或处理完后再放回去，然后抽下一个。在实际的工作中通常我们很少会这样抽，一般都属于无放回抽样，这时候需要用超几何分布来计算概率。在一般的教课书上都会要求，当总体的容量N不大时，要用超几何分布来计算，如果N很大而n很小，则可以用二项分布来近似计算，也就是可以将无放回抽样近似看出有放回抽样。至于n要小到什么程度，有的书上说n/N小于0.1就可以了，有的书上则要求小于0.05。

！0-1 分布 是 n = 1 时的特殊二项分布

泊松分布

取值是无限个+可数个
白话一点就是 0 到无限个，例如：

• 某人一天收到的微信数量
• 来到火车站的乘客

泊松分布跟二项分布也有联系，当n很大，单次概率p很小的时候，两者近似。

几何分布

分布函数