1. 参数估计的基本原理
估计量与估计值
例如:样本均值 ,这里的
就是估计量,80 是估计值。
估计量有样本均值、样本比例、样本方差等
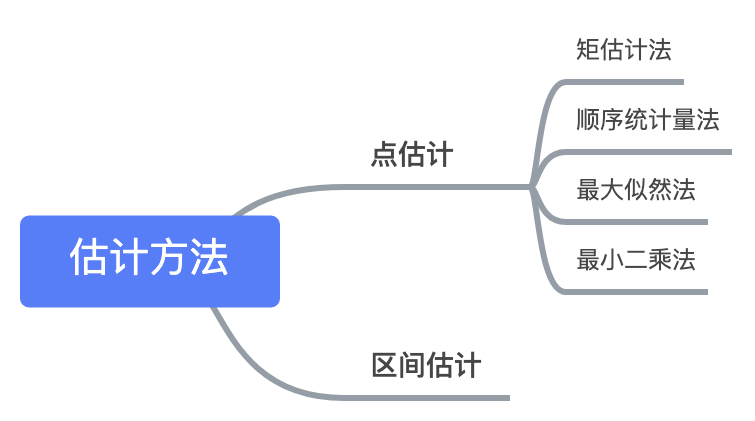
估计方法
A. 点估计
用样本的估计值直接作为总体参数的估计值
如:用样本均值直接作为总体均值
缺点:不知道样本估计值与总体参数之间的差距
B. 区间估计
在点估计的基础上,给出总体参数估计的一个区间范围。该区间由样本统计量加减抽样误差而得到的。
例如:当描述一个人的体重时, 你一般可能不会说这个人是 76.45 公斤, 而说这个人是七八十公斤(70公斤-80公斤)。你提供的这个范围就是某种区间估计。
为了估计某候选人在选民中的支持率(即总体比例 p),调查机构的民意测验可能会说,该候选人的“支持率为 75%, 误差是 ±3 %, 置信度为 95%”。 这种说法意味着下面三点:
- 样本中的支持率为 75%,这是用样本比例作为对总体比例的点估计。
- 估计范围为 75% ± 3%(±3%的误差), 即区间(72%, 78%)。
- 如果用类似的方式,重复抽取大量(样本量相同的)样本时,产生的大量类似区间中有些会覆盖真正的 p,而有些不会,但这些区间中大约有 95% 会覆盖真正的总体比例。
这样得到的区间被称为总体比例 p 的置信度(confidence level)为 95% 的置信区间(confidence interval)。这里的置信度又称置信水平或置信系数。
显著性水平 置信水平
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,用α表示。显著性是对差异的程度而言的,程度不同说明引起变动的原因也有不同。
置信度 = 1-α,其表明了区间估计的可靠性。
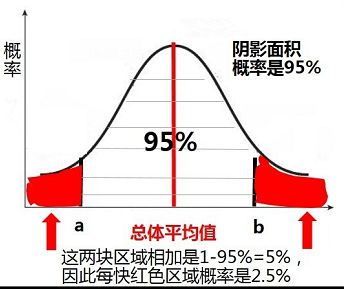
错误:置信度为 95%,也就是说 95% 的样本都落在了阴影里。
这句话说是错误的,但我没懂。
如何评价估计量的优良性
无偏性:估计量抽样分布的数学期望 = 被估计的总体参数
有效性:对同一总体参数给出的两个无偏点估计量,有更小标准差的更有效
一致性:随着样本容量的增大,估计量的值越来越接近于总体参数
2. 一个总体参数
总体参数 符号表示 样本统计量
均值
比例
方差
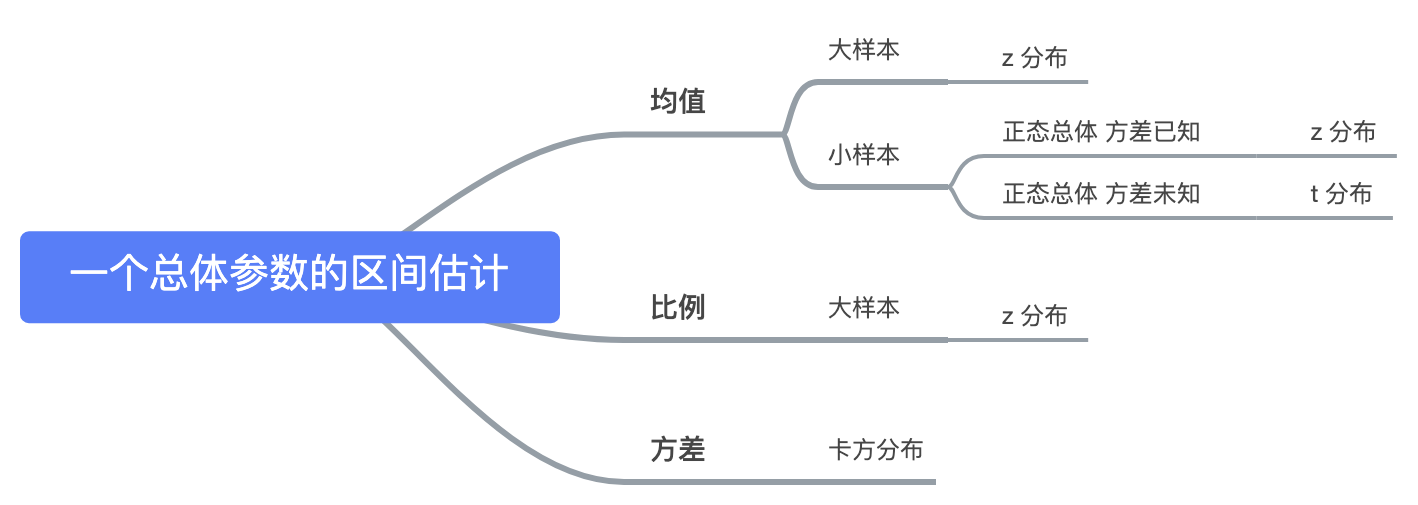
总体均值 的区间估计
确定前提条件:
- 是否正态分布?
- 方差是否已知?
- 小样本还是大样本?(样本量 ≥30 是大样本,这是是统计学家的经验得出的)
情况 1:服从正态分布,方差已知
(这里的 z 是正态分布统计量)
情况 2:方差未知,大样本。不服从正态分布,但可以用正态分布来近似。
Q:一批食品中随机抽取 25 袋,测得每袋重量如下图:
我们已经知道产品重量分布服从正态分布,且总体标准差为 10g。 要求估计该批产品平均重量的置信区间,置信水平为 95%。
A:使用上面第一种情况的公式

很容易算出来
标准差给出了是 10 置信水平 90% 所以
= 1-95% = 0.05
是正态分布统计量,
需要从正态分布表来查,是 1.96 (这个很常见,需要记住) n 是样本量 25 所以置信区间为
Q:一家保险公司随机抽取了 36 个投保人的年龄如下,请建立投保人年龄 90%的置信区间。
A:根据第二个公式
已知
计算可得
这里不知道总体标准差
,所以需要自己算样本标准差

情况 3:服从正态分布,总体方差未知,小样本
这里就需要用 t 分布统计量了 ,而计算公式为
t 分布与正态分布(z 分布)
t 分布是类似正态分布的一种对称分布,通常比正态分布平坦和分散(因为 t 分布方差更大)。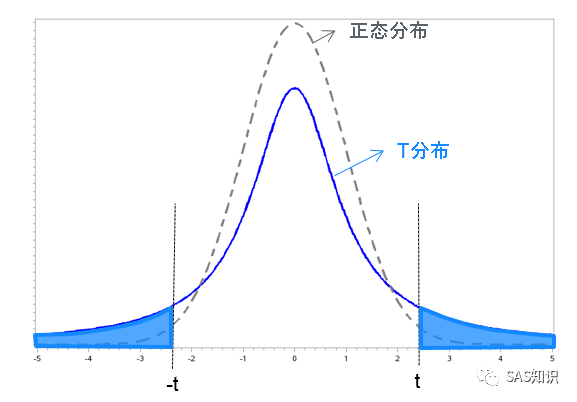
t 分布只依赖于自由度,当自由度增大,分布也会逐渐趋向正态分布。
Q:已知灯泡寿命服从正态分布,抽取 16 只,测得寿命如下:
建立置信区间为 95% 的置信区间。
A:是小样本,因此
t 这里可以查 t 分布表。
总体比例
条件:
- 总体服从二项分布
- 可以由正态分布来近似
(样本比例 ± 统计误差)
样本比例
总体比例
Q:从某公司随机抽取 100 人,其中女性 65 人。请以 95% 的置信水平估计总体中女性比例的置信区间。
A:已知

总体方差
挖坑代填
Q:一批食品中随机抽取 25 袋,测得每袋重量如下图:
我们已经知道产品重量分布服从正态分布,以 95% 的置信水平,测算该种食品重量方差的置信区间。
A:已知
,那么计算卡方分布的上下两个分位数点。
置信区间为
所以标准差的置信区间为 7.54g-13.43g。
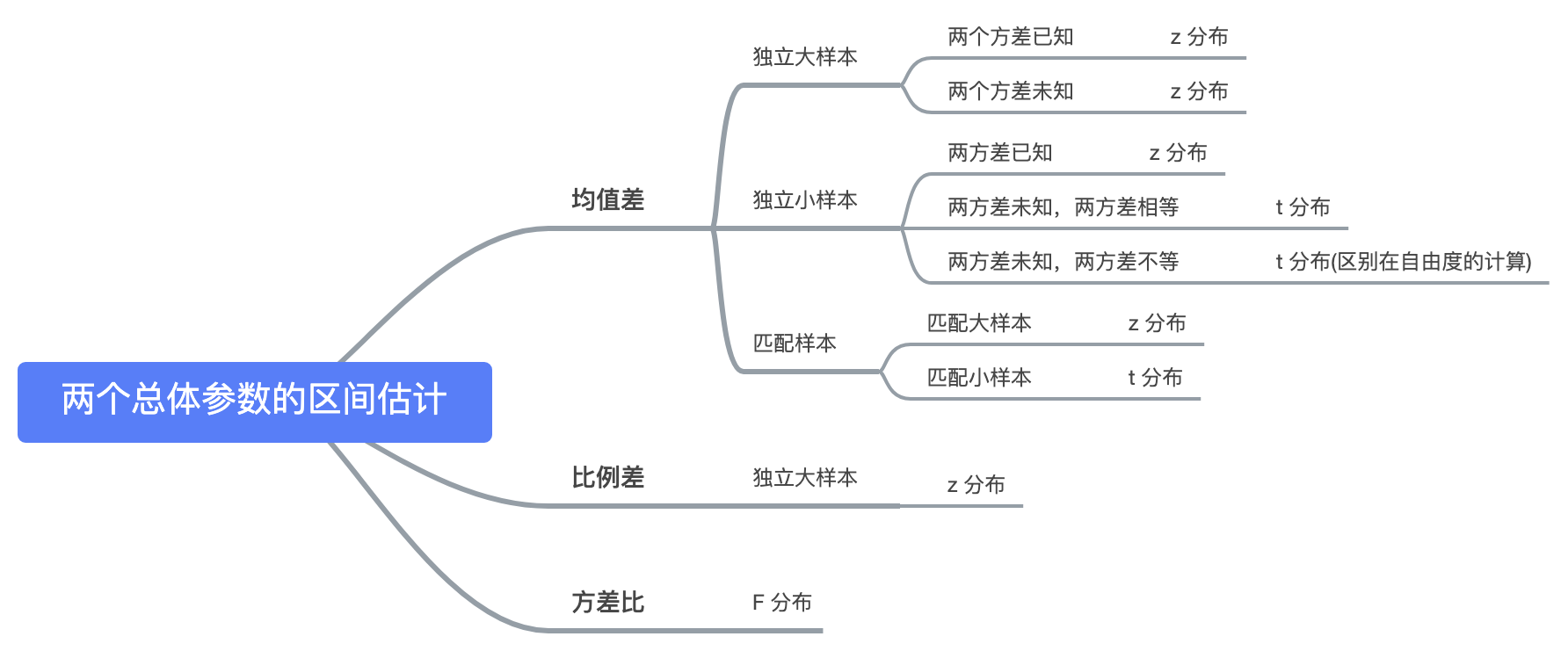
3. 两个总体参数
总体参数 符号表示 样本统计量
均值之差
比例之差
方差比
两个总体均值之差
挖坑代填 https://www.bilibili.com/video/av49829030/?p=12
两个总体比例之差
两个总体方差比
参考文献:
https://zhuanlan.zhihu.com/p/36077458
https://www.bilibili.com/video/av49829030/?p=11