方差

方差：描述离散程度

方差是反应随机变量波动性的数据特征。
考察随机变量对于其均值的偏差，可以用绝对值，但是数学上绝对值不好用，因此采用的平方的形式。

方差开方后，用 σ 表示，叫做 标准差 或 均方差。

方差 or 标准差较小，说明随机变量较集中。

方差与期望的区别

两个人去射箭，箭的位置分布如下：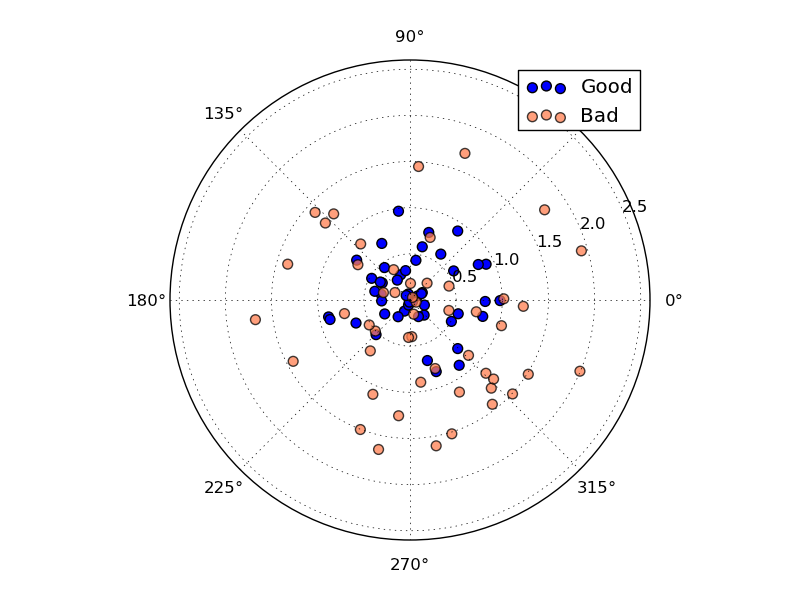

尽管两套落点的平均中心位置都在原点 (即期望相同），但两套落点的离散程度明显有区别。蓝色的点离散程度更小。可见，方差是独立于期望的另一个对分布的度量。两个分布，完全可能有相同的 期望，而方差不同，正如我们上面的箭靶。

方差与标准差的区别

区别在量纲上。标准差与随机变量，以及随机变量的期望是同量纲的。（这句没听懂）因此在现实生活中标准差用得更多。