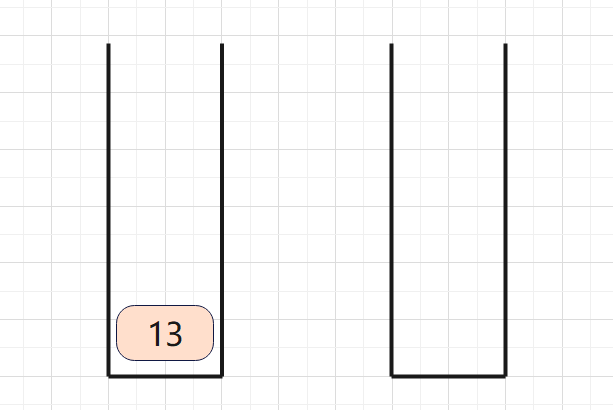
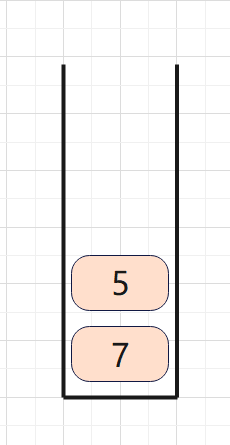
前缀表达式（波兰表达式）

前缀表达式又称波兰式，前缀表达式的运算符位于操作数之前。例如 (3+4)*5-6对应的前缀表达式就是- * + 3 4 5 6

思路

从右至左扫描表达式，遇到数字就压入栈中，遇到运算符时，弹出栈顶的两个数，用运算符对他们做相应的运算，，并将结果入栈，重复，直到表达式最左端，最后运算的得出的值就是表达式的结果。

如上例子：从右往左扫描，将6，5，4，3压入栈中
image.png
再次扫描下一个遇到+，就pop两数3和4进行加法运算，得到结果后又入栈

注：num1是栈顶元素，num2是次顶元素，num1 符号 num2

image.png
直到最后栈中就剩下一个值，就是结果

中缀表达式

操作符号在中间，例如普通的算式3+4-8*2/4。中缀表达式对于人来说很好操作，对于计算机来说不太好，因为运算次序问题。一般计算都是转换成后缀表达式

思路

使用栈完成表达式的计算思路

  1. 定义两个栈，一个用来放数字，numStack，一个用来放操作符，operStack
  2. 定义一个index指针，字符串的索引
  3. 遍历字符串，发现index指向一个数字，就直接入numStack
  4. index指向一个符号，就分以下情况
    1. 如果发现符号栈为空，就直接入栈
    2. 如果符号栈有操作符，就进行比较，如果当前的操作符的优先级小于或等于栈中的操作符号，就需要从数栈中pop出两个数（出栈的第二个数是运算式子的第一个数字），从符号栈中pop出一个符号，进行运算，将得到的结果入数栈，然后将当前的操作符入符号栈，如果当前的操作符优先级大于栈中的操作符，就直接入符号栈。
  5. 当表达式字符串扫描完毕了，就顺序的从数栈和符号栈中pop出相应的数和符号，并运算
  6. 最后在数栈只有一个数字，就是表达式的结果

图解

3+26-2图解如下
image.png![image.png](https://cdn.nlark.com/yuque/0/2022/png/21464164/1641998326346-015f2f97-37e9-4711-82ad-ad2cd7e9e2d7.png#clientId=u1dafbee5-4ecd-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=292&id=zEwui&margin=%5Bobject%20Object%5D&name=image.png&originHeight=583&originWidth=579&originalType=binary&ratio=1&rotation=0&showTitle=true&size=15070&status=done&style=none&taskId=ub8d8f645-4c52-49cc-9535-a2ce30bd71c&title=index%E6%8C%87%E5%90%91-%E5%8F%B7%E6%97%B6%EF%BC%8C-%E6%AF%94%2A%E4%BC%98%E5%85%88%E7%BA%A7%E4%BD%8E%EF%BC%8C%E5%8F%96%E5%87%BA%E4%B8%A4%E4%B8%AA%E6%95%B0%E5%92%8C%2A%E5%8F%B7%EF%BC%8C%E8%BF%90%E7%AE%97%E5%90%8E%E7%BB%93%E6%9E%9C%E6%94%BE%E6%95%B0%E6%A0%88&width=289.5 “index指向-号时，-比优先级低，取出两个数和*号，运算后结果放数栈”)image.pngimage.png

注意：图解理论如此，其实就是从右往左算，纯图解有bug，代码解决了bug

代码

注意这个简单的中缀计算器，不能计算小数，负数等

  1. using System;
  2. using System.Collections.Generic;
  4. namespace ConsoleApp1
  5. {
  6.     class Program
  7.     {
  8.         static void Main(string[] args)
  9.         {
  10.             string expression = "3456-23/456-56+34-23/23-12+3";
  11.             //定义两个栈，数栈和符号栈
  12.             ArrayStack<int> numStack = new ArrayStack<int>(10);
  13.             ArrayStack<string> operStack = new ArrayStack<string>(10);
  14.             //定义需要的相关变量
  15.             int index = 0;//表达式的索引
  16.             int num1 = 0;//先出栈的数
  17.             int num2 = 0;//后出栈的数
  18.             string oper = "";//操作符
  19.             int res = 0;//运算结果
  21.             //扫描表达式
  22.             while (true)
  23.             {
  24.                 //记录一下是数字还是操作符，因为index是引用的，这个r要多次用到，就要用变量存着
  25.                 string r = convertNumOper(ref index, expression);
  26.                 int stackpeak = numStack.peak();
  27.                 string operpeak = operStack.peak();
  28.                 if (isOper(r))//如果是运算符
  29.                 {
  30.                     //判断当前的符号栈是否为空
  31.                     if (!operStack.isEmpty())
  32.                     {
  33.                         //如果符号栈中有操作符，就进行比较，如果当前的操作符的优先级小于或者等于栈中的操作符，就需要从数栈中pop出两个数
  34.                         //再从符号站中pop出两个符号进行运算，将得到结果，入数栈，然后将当前的操作符入符号栈
  35.                         if (priority(r) <= priority(operStack.peak()))
  36.                         {
  37.                             num1 = numStack.pop();
  38.                             num2 = numStack.pop();
  39.                             oper = operStack.pop();
  40.                             //前面一个操作符号是减法，如7-2-3，应该变成7-(2-(-3))
  41.                             if ((oper == "-" ||oper=="+")&& operStack.peak() == "-")
  42.                                 num1 = 0 - num1;
  43.                             res = cal(num1, num2, oper);
  44.                             //把运算的结果如数栈
  45.                             numStack.push(res);
  46.                             //然后把当前的操作符入符号栈
  47.                             operStack.push(r);
  48.                         }
  49.                         else//如果当前操作符的优先级大于栈顶的操作符，就直接入符号栈
  50.                         {
  51.                             operStack.push(r);
  52.                         }
  53.                     }
  54.                     else//如果为空直接入栈
  55.                     {
  56.                         operStack.push(r);
  57.                     }
  58.                 }
  59.                 else//如果是数，则直接入数栈
  60.                 {
  61.                     numStack.push(Convert.ToInt32(r));
  62.                 }
  63.                 //index如果到了最后就退出while
  64.                 if (index >= expression.Length)
  65.                     break;
  66.             }
  68.             //表达式扫描完毕，就顺序的从数栈和符号栈中pop出相应的数和符号，并运行
  69.             while (true)
  70.             {
  71.                 //如果符号栈为空，则计算到最后的结果，数栈中只有一个数字【结果】
  72.                 if (operStack.isEmpty())
  73.                 {
  74.                     break;
  75.                 }
  76.                 num1 = numStack.pop();
  77.                 num2 = numStack.pop();
  78.                 oper = operStack.pop();
  80.                 //前面一个操作符号是减法，如7-2-3，应该变成7-(2-(-3))
  81.                 if ((oper == "-" || oper == "+") && operStack.peak() == "-")
  82.                     num1 = 0 - num1;
  83.                 res = cal(num1, num2, oper);
  84.                 //把运算的结果如数栈
  85.                 numStack.push(res);
  86.             }
  88.             //到这里数栈就一个数了，就是结果
  89.             Console.WriteLine($"{expression}={numStack.pop()}");
  91.         }
  92.         //返回一个数字或者操作符的字符串
  93.         static string convertNumOper(ref int index,string expression)
  94.         {
  95.             string r = "";
  96.             while (true)
  97.             {
  98.                 if (index >= expression.Length)
  99.                     break;
  100.                 if (expression[index] >= 48 && expression[index] <= 57)//数字
  101.                 {
  102.                     r += expression[index++];
  103.                 }
  104.                 else//是操作符
  105.                 {
  106.                     if (r != "")//如果r不等于空，说明前面有数字，现在到了操作符，为了保证r是纯数就退出了，index不++
  107.                         break;
  108.                     else//如果r等于空，这次调用方法index第一个指向符号，把符号取出来后，index++，就退出循环
  109.                     {
  110.                         r += expression[index++];
  111.                         break;
  112.                     }
  114.                 }
  115.             }
  116.             return r;
  117.         }
  119.         //返回运算符的优先级，优先级是人为确定的，优先级使用数字表示，数字越大则优先级越高
  120.         static int priority(string oper)
  121.         {
  122.             if (oper == "*" || oper == "/")
  123.             {
  124.                 return 1;
  125.             }
  126.             else if (oper == "+" || oper == "-")
  127.             {
  128.                 return 0;
  129.             }
  130.             return -1;//目前只有+-*/
  131.         }
  132.         //判断是不是一个运算符
  133.         static bool isOper(string val)
  134.         {
  135.             return val == "+" || val == "-" || val == "*" || val == "/";
  136.         }
  137.         //计算方法
  138.         static int cal(int num1, int num2, string oper)
  139.         {
  140.             int res = 0;//计算的结果
  141.             switch (oper)
  142.             {
  143.                 //注意顺序，后传出来的数作为运算式子的第一个
  144.                 case "+": res = num2 + num1; break;
  145.                 case "-": res = num2 - num1; break;
  146.                 case "*": res = num2 * num1; break;
  147.                 case "/": res = num2 / num1; break;
  148.             }
  149.             return res;
  150.         }
  152.     }
  153. }

后缀表达式（逆波兰表达式）

和前缀表达式相似，只是运算符位于操作数之后，例如(3+4)*5-6对应的后缀表达式就是3 4 + 5 * 6 -

思路

从左至右扫描表达式，遇到数字时，就将数字压入栈中，遇到运算符时，pop两个数就行运算，得到结果又入栈，重复，直到最右端，最后运算出来的值就是表达式的结果

如上例子，从左往右扫，将3 ，4压入栈中
image.png
然后遇到了符号，pop两个数字，进行符号运算，得到结果入栈

注：num1是栈顶元素，num2是次顶元素，num2 符号 num1

image.png
直到最后剩下一个值，就是结果

代码

  1. using System;
  2. using System.Collections.Generic;
  4. namespace ConsoleApp1
  5. {
  6.     class Program
  7.     {
  8.         static void Main(string[] args)
  9.         {
  10.             //逆波兰表达式，数字和符号用空格隔开
  11.             string expression = "3 4 + 5 * 6 -";
  12.             ArrayStack<int> stack = new ArrayStack<int>(10);
  13.             string[] exarr = expression.Split(" ");//直接分隔
  14.             for(int i = 0; i < exarr.Length; i++)
  15.             {
  16.                 try
  17.                 {
  18.                     //如果转换成数字发生了异常就说明是符号
  19.                     stack.push(Convert.ToInt32(exarr[i]));
  20.                 }
  21.                 catch
  22.                 {
  23.                     //出两个数，计算结果，把结果入栈
  24.                     int num1 = stack.pop();
  25.                     int num2 = stack.pop();
  26.                     int result = cal(num1, num2, exarr[i]);
  27.                     stack.push(result);
  28.                 }
  29.             }
  30.             //最后栈中就剩一个值了，就是结果
  31.             Console.WriteLine(stack.pop());
  32.         }
  33.         //计算方法
  34.         static int cal(int num1, int num2, string oper)
  35.         {
  36.             int res = 0;//计算的结果
  37.             switch (oper)
  38.             {
  39.                 //注意顺序，后传出来的数作为运算式子的第一个
  40.                 case "+": res = num2 + num1; break;
  41.                 case "-": res = num2 - num1; break;
  42.                 case "*": res = num2 * num1; break;
  43.                 case "/": res = num2 / num1; break;
  44.             }
  45.             return res;
  46.         }
  47.     }
  48. }

前后缀表达式与中缀表达式区别

中缀表达式存在计算次序的问题，而波兰与逆波兰就没有这个问题

中缀表达式转成后缀表达式

思路

  1. 初始化两个栈：运算符栈s1和存储中间结果的栈s2
  2. 从左至右扫描中缀表达式
  3. 遇到操作数时，将其push入s2
  4. 遇到括号时：
    1. 如果是左括号，则直接push入s1
    2. 如果是右括号，则依次pop出s1栈顶的运算符，并push入s2，直到遇到左括号为止，此时将这一对括号丢弃
  5. 遇到运算符时，比较与s1顶运算符的优先级
    1. 如果s1为空，或栈顶运算符为左括号，则直接将此运算符入栈；
    2. 否则如果，当前运算符的优先级比栈顶运算符的高，也将运算符push入s1；
    3. 否则如果，当前运算符优先级<=栈顶的运算符的优先级，将s1栈顶的运算符pop出来，push到s2
      1. 再次来到5.a这一步，当前运算符与s1中新的栈顶的运算符相比较
  6. 重复步骤2至5，直到表达式的最右边
  7. 将s1中剩余的运算符依次弹出并压入s2
  8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

    代码

    中缀表达式转后缀表达式的核心方法InfixToSuffix ```csharp using System; using System.Collections.Generic;

namespace ConsoleApp1 { class Program { static void Main(string[] args) {

  1.         //中缀表达式
  2.         string infixExpression = "32+3*(7-2*(1+2))-3+12/4";
  3.         //逆波兰表达式，数字和符号用空格隔开
  4.         string suffixExpression = InfixToSuffix(infixExpression);
  5.         ArrayStack<int> stack = new ArrayStack<int>(10);
  6.         string[] exarr = suffixExpression.Split(" ");//直接分隔
  7.         for (int i = 0; i < exarr.Length; i++)
  8.         {
  9.             try
  10.             {
  11.                 //如果转换成数字发生了异常就说明是符号
  12.                 stack.push(Convert.ToInt32(exarr[i]));
  13.             }
  14.             catch
  15.             {
  16.                 //出两个数，计算结果，把结果入栈
  17.                 int num1 = stack.pop();
  18.                 int num2 = stack.pop();
  19.                 int result = cal(num1, num2, exarr[i]);
  20.                 stack.push(result);
  21.             }
  22.         }
  23.         Console.WriteLine(infixExpression);
  24.         Console.WriteLine(suffixExpression);
  25.         //最后栈中就剩一个值了，就是结果
  26.         Console.WriteLine(stack.pop());
  27.     }
  28.     //中缀表达式转换后缀表达式，传入一个中缀表达式
  29.     static string InfixToSuffix(string expression)
  30.     {
  31.         int index = 0;//扫描指针
  32.         //1.初始化两个栈
  33.         ArrayStack<string> s1 = new ArrayStack<string>(100);//符号栈
  34.         ArrayStack<string> s2 = new ArrayStack<string>(100);//数字栈
  35.         //2.从左往右扫描中缀表达式
  36.         while (true)
  37.         {
  38.             string r = convertNumOper(ref index, expression);
  39.             //3.如果是操作数就直接push到s2
  40.             if (!isOper(r))
  41.             {
  42.                 s2.push(r);
  43.             }
  44.             //4.遇到括号时
  45.             //4.a 如果是左括号，则直接push入s1
  46.             else if (r == "(")
  47.             {
  48.                 s1.push(r);
  49.             }
  50.             //4.b 如果是右括号，则依次弹出s1栈顶的运算符，并push入s2，直到遇到左括号为止，此时将这一对括号丢弃
  51.             else if (r == ")")
  52.             {
  53.                 while (true)
  54.                 {
  55.                     string a = s1.pop();
  56.                     if (a != "(")
  57.                         s2.push(a);
  58.                     else
  59.                         break;
  60.                 }
  61.             }
  62.             //5.遇到运算符时，比较与s1顶运算符的优先级
  63.             else
  64.             {
  65.                 while (true)
  66.                 {
  67.                     //5.a 如果s1为空，或者栈顶运算符为左括号，则直接将此运算符入栈
  68.                     if (s1.isEmpty() || s1.peak() == "(")
  69.                     {
  70.                         s1.push(r);
  71.                         break;
  72.                     }
  73.                     //5.b 当前运算符的优先级比栈顶运算符的高，也将运算符push入s1
  74.                     else if (priority(r) > priority(s1.peak()))
  75.                     {
  76.                         s1.push(r);
  77.                         break;
  78.                     }
  79.                     //5.c 当前运算符优先级<=栈顶的运算符的优先级，将s1栈顶的运算符pop出来，push到s2
  80.                     else if (priority(r) <= priority(s1.peak()))
  81.                     {
  82.                         s2.push(s1.pop());
  83.                     }
  84.                     //5.d.i 再次来到5.a这一步，当前运算符与s1中新的栈顶的运算符相比较
  85.                 }
  86.             }
  87.             //6.重复2至5步，直到表达式的最右边
  88.             if (index >= expression.Length)
  89.                 break;
  91.         }
  92.         //7.将s1中剩余的运算符依次弹出并压入s2
  93.         while (true)
  94.         {
  95.             if (s1.isEmpty())
  96.                 break;
  97.             s2.push(s1.pop());
  98.         }
  99.         //8.依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式
  100.         string suffixstr = "";
  101.         while (true)
  102.         {
  103.             if (s2.isEmpty())
  104.                 break;
  105.             string t = s2.pop();
  106.             suffixstr = t + " " + suffixstr;
  107.         }
  108.         return suffixstr.Trim();//去掉两端的空格
  109.     }
  110.     //返回一个数字或者操作符的字符串
  111.     static string convertNumOper(ref int index, string expression)
  112.     {
  113.         string r = "";
  114.         while (true)
  115.         {
  116.             if (index >= expression.Length)
  117.                 break;
  118.             if (expression[index] >= 48 && expression[index] <= 57)//数字
  119.             {
  120.                 r += expression[index++];
  121.             }
  122.             else//是操作符
  123.             {
  124.                 if (r != "")//如果r不等于空，说明前面有数字，现在到了操作符，为了保证r是纯数就退出了，index不++
  125.                     break;
  126.                 else//如果r等于空，这次调用方法index第一个指向符号，把符号取出来后，index++，就退出循环
  127.                 {
  128.                     r += expression[index++];
  129.                     break;
  130.                 }
  132.             }
  133.         }
  134.         return r;
  135.     }
  136.     //计算方法
  137.     static int cal(int num1, int num2, string oper)
  138.     {
  139.         int res = 0;//计算的结果
  140.         switch (oper)
  141.         {
  142.             //注意顺序，后传出来的数作为运算式子的第一个
  143.             case "+": res = num2 + num1; break;
  144.             case "-": res = num2 - num1; break;
  145.             case "*": res = num2 * num1; break;
  146.             case "/": res = num2 / num1; break;
  147.         }
  148.         return res;
  149.     }
  150.     //判断是不是一个运算符
  151.     static bool isOper(string val)
  152.     {
  153.         return val == "+" || val == "-" || val == "*" || val == "/"||val=="("||val==")";
  154.     }
  155.     //返回运算符的优先级，优先级是人为确定的，优先级使用数字表示，数字越大则优先级越高
  156.     static int priority(string oper)
  157.     {
  158.         if (oper == "*" || oper == "/")
  159.         {
  160.             return 1;
  161.         }
  162.         else if (oper == "+" || oper == "-")
  163.         {
  164.             return 0;
  165.         }
  166.         return -1;//目前只有+-*/
  167.     }
  170. }

}

```