基本介绍
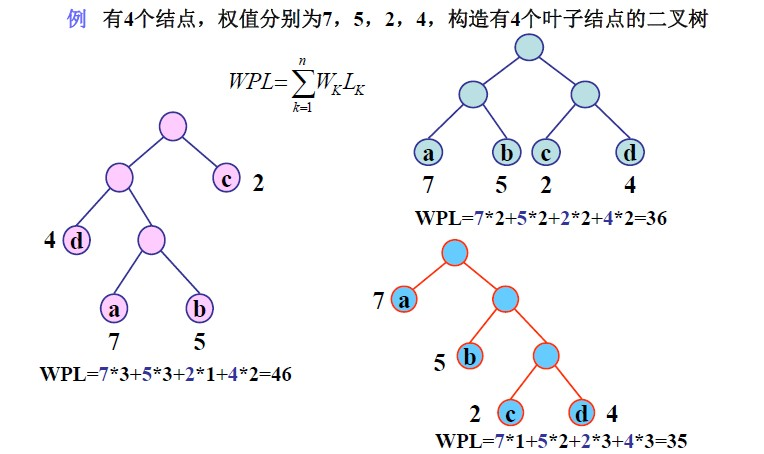
给定n个权值作为n个叶子节点,构造一颗二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也叫赫夫曼树(Huffman Tree)
赫夫曼树是带权路径最短的树,权值较大的节点离根节点较近。
赫夫曼树的几个重要概念
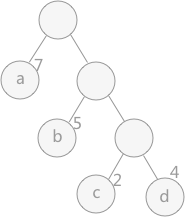
- 路径:在一棵树中,一个节点到另一个节点之间的通路,称为路径。下图中,从根节点到节点 a 之间的通路就是一条路径。
- 路径长度:在一条路径中,每经过一个节点,路径长度都要加 1 。例如在一棵树中,规定根节点所在层数为1层,那么从根节点到第 i 层节点的路径长度为 i - 1 。下图中从根节点到节点 c 的路径长度为 3。
- 节点的权:给每一个节点赋予一个新的数值,被称为这个节点的权。例如,下图中节点 a 的权为 7,结点 b 的权为 5。
- 节点的带权路径长度:指的是从根节点到该节点之间的路径长度与该节点的权的乘积。例如,图 1 中结点 b 的带权路径长度为
2 * 5 = 10。 - 树的带权路径长度(WPL):树的带权路径长度为树中所有叶子节点的带权路径长度之和。下图中WPL为
1*7+2*5+3*2+3*4=35。权值越大的节点离根节点越近的二叉树才是最优叉树
创建赫夫曼树思路
- 对数据进行从小到大排序,每一个数据都是一个节点,每个节点可以看成是一颗最简单的二叉树(只有根结点,没有左右子节点)
- 取出根节点权值最小的两颗二叉树(数据中前两个数)
- 用这两棵树组成一个新的二叉树,该新的二叉树的根节点的权值是这两颗二叉树根节点的权值的和
- 再将这颗新的二叉树,以根节点的权值大小和剩下的数据再次排序
不断的重复1,2,3,4的步骤,直到数列中,所有数据都被处理,就得到一颗赫夫曼树
创建赫夫曼树图解
现在有一个数组
34,62,11,5,47,每个数据都可以看作是一个节点,对这些数据进行排序

- 取出根节点的前两棵树,组成一颗新的二叉树,新的二叉树的根节点的权值是前两棵树权值的和。然后再将这颗二叉树根节点的权值进行从新排序,16正好排在34前面
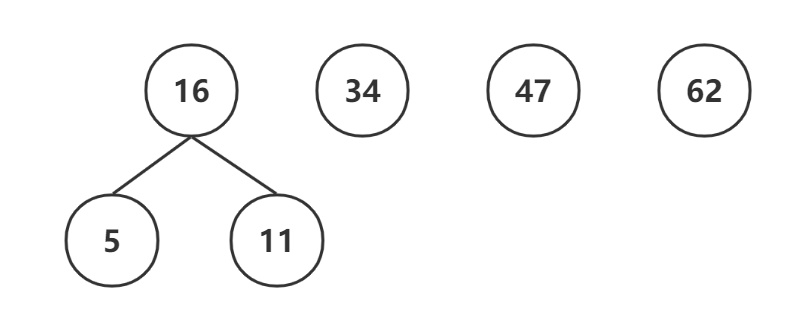
- 16和34又组成一颗新的二叉树,新根节点的权值为50,50在47和62之间

- 47和50又组成一颗新的二叉树,新的根节点为97,97在62后面
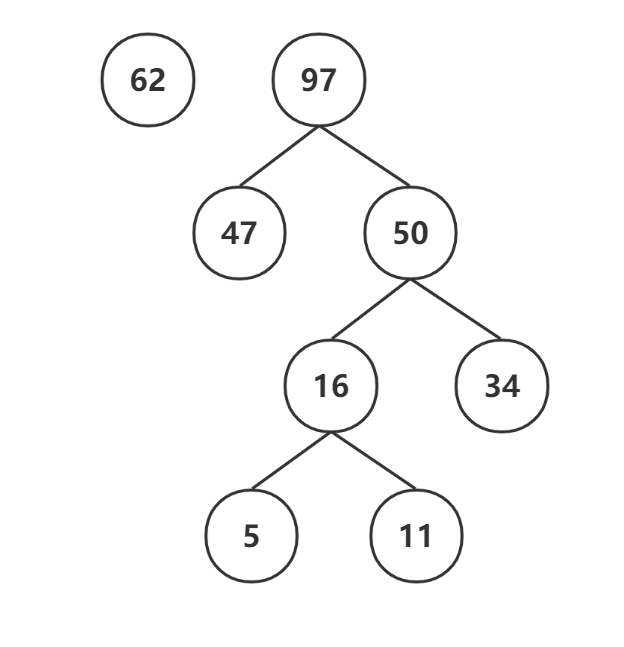
- 62和97又组成一颗新的二叉树,这次全部数据都使用了,所以这就是最终的赫夫曼树
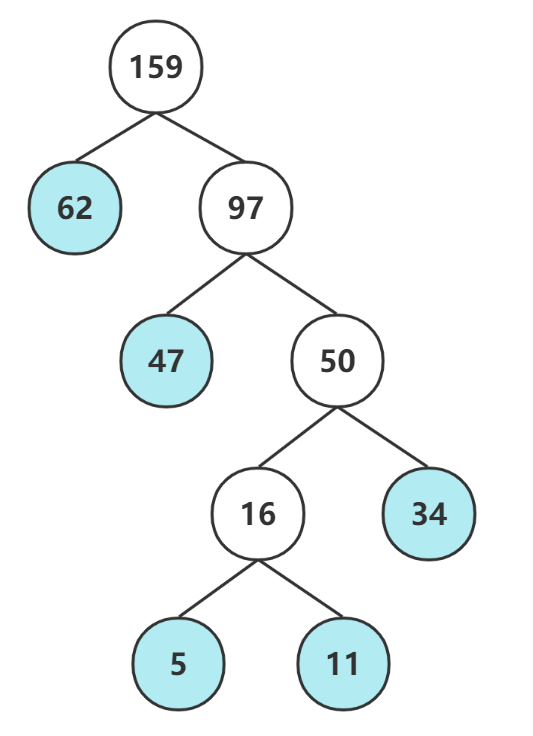
创建赫夫曼树代码
```csharp using System; using System.Collections.Generic;
namespace ConsoleApp1 { class Program {
static void Main(string[] args){int[] arr = { 13,7,8,3,29,6,1};HFNode hfnode = CreateHuffmanTree(arr);hfnode.preOrder();}//创建赫夫曼树public static HFNode CreateHuffmanTree(int[] arr){//将数据变成节点装进listList<HFNode> hfnodes = new List<HFNode>();foreach (var a in arr){hfnodes.Add(new HFNode(a));}//处理完的节点不断从列表中删除,最后当列表只有一个数据时,就说明处理完成了,赫夫曼树形成while (hfnodes.Count > 1){//1.对节点集合进行权值从小到大排序hfnodes.Sort();//2.取出最小的两个节点,左右新二叉树的左右子节点HFNode leftnode = hfnodes[0];HFNode rightnode = hfnodes[1];//3.构建一颗新的二叉树,这个二叉树的根节点的权值等于左右子节点之和HFNode parent = new HFNode(leftnode.value + rightnode.value);//4.把这颗树的左右节点挂起来parent.left = leftnode;parent.right = rightnode;//5.从hfnodes中删除已经用过的节点hfnodes.Remove(leftnode);hfnodes.Remove(rightnode);//6.将parent加入hfnodeshfnodes.Add(parent);}//返回赫夫曼树的根节点return hfnodes[0];}/// <summary>/// 赫夫曼节点实现IComparable接口,作用是进行排序/// </summary>public class HFNode : IComparable<HFNode>{public int value;//节点的权值public HFNode left;public HFNode right;public HFNode(int value){this.value = value;}//实现接口方法public int CompareTo(HFNode hfnode){//从小到大排序return this.value - hfnode.value;}//前序遍历public void preOrder(){Console.WriteLine(this.value);if (this.left != null)this.left.preOrder();if (this.right != null)this.right.preOrder();}}}
}
```