前面讲到了二叉搜索树 (BST) 和二叉平衡树 (AVL) ，二叉搜索树在最好的情况下搜索的时间复杂度为 O(logn) ，但如果插入节点时，插入元素序列本身就是有序的，那么BST树就退化成一个线性表了，搜索的时间复杂度为 O(n)。
如果想要减少比较次数，就需要降低树的高度。在插入和删除节点时，要保证插入节点后不能使叶子节点之间的深度之差大于 1，这样就能保证整棵树的深度最小，这就是AVL 树解决 BST 搜索性能降低的策略。但由于每次插入或删除节点后，都可能会破坏 AVL 的平衡，而要动态保证 AVL 的平衡需要很多操作，这些操作会影响整个数据结构的性能，除非是在树的结构变化特别少的情形下，否则 AVL 树平衡带来的搜索性能提升有可能还不足为了平衡树所带来的性能损耗。
因此，引入了 2-3 树来提升效率。

2-3树定义

  1. 2-3 树要么为空要么具有以下性质：
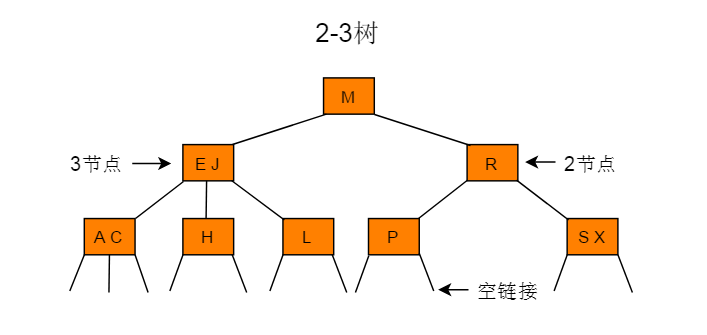
  2. 2-3树所有叶子节点都在同一层（主要是B树都满足这个条件）
  3. 有两个子节点的节点叫二节点，二节点要么没有子节点，要么有两个子节点。有一个数据域和两个子节点指针。当前节点的数据的值要大于左子树中所有节点的数据，要小于右子树中所有节点的数据。
  4. 有三个子节点的节点叫三节点，三节点要么没有子节点，要么有三个子节点。有两个数据域 a 和 b 和三个子节点指针。左子树中所有的节点数据要小于a，中子树中所有节点数据要大于 a 而小于 b ，右子树中所有节点数据要大于 b
  5. 2-3树是由二节点和三节点构成的树

image.png