堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，堆排序是不稳定的排序。

什么是堆？

堆是具有以下性质的完全二叉树：

  1. 每个节点的值都大于或者等于其左右子节点的值，称为大顶堆
  2. 每个节点的值都小于或者等于其左右子节点的值，称为小顶堆

大顶堆和小顶堆示意图
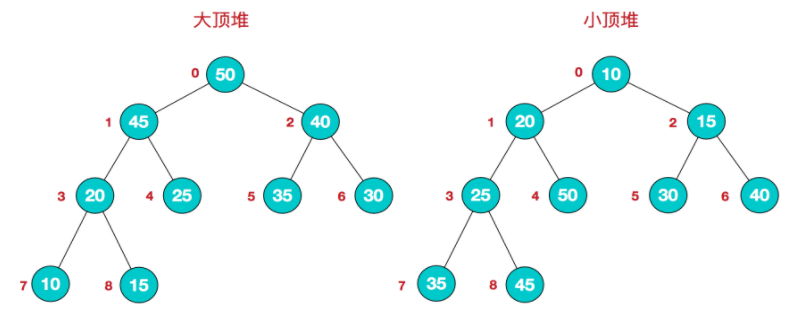
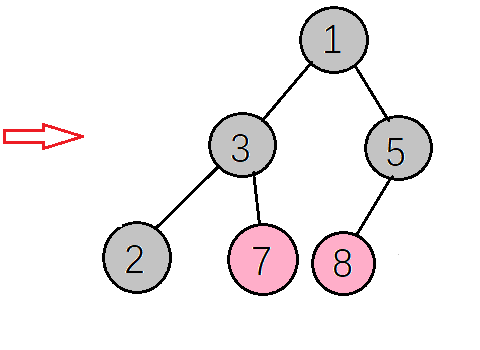
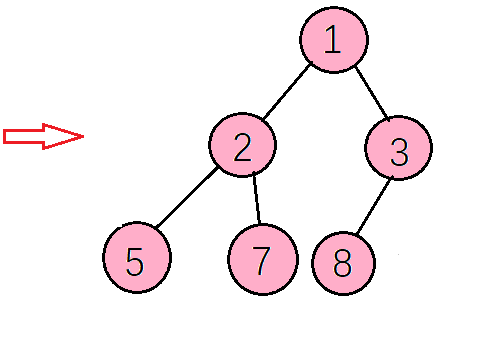
如下图，对大顶堆中的节点按层进行编号，映射到数组中就是下面这个样子
堆排序 - 图2
堆其实就是利用完全二叉树的结构来维护的一维数组

公式

  • 大顶堆：arr[i]>=arr[2*i+1]&&arr[i]>=arr[2*i+2]，i对应的第几个节点，数组的下标
  • 小顶堆：arr[i]<=arr[2*i+1]&&arr[i]<=arr[2*i+2]

    这个公式可以看顺序存储二叉树那篇文章

升序与降序

升序采用大顶堆，降序采用小顶堆

为什么升序用大顶堆

上面提到过大顶堆的特点：每个节点的值都大于或等于其左右子节点的值，我们把大顶堆构建完毕后根节点的值一定是最大的，然后把根节点的和最后一个元素（也可以说最后一个节点）交换位置，那么末尾元素此时就是最大元素了。

思路

升序排列的思路

  1. 先n个元素的无序序列，构建成大顶
    1. 构建大顶堆的方法：
    2. 先顺序存储二叉树
    3. 然后找到最后一个非叶子节点，数组长度/2-1=y，y就是最后一个非叶子节点的下标
    4. 比较这个节点和其左右子节点的大小，找到最大的一个数和当前的非叶子节点交换
    5. 然后y-1得到倒数第二个非叶子节点，同样的比较该节点和其左右子节点，找出最大的和y-1这个节点交换
    6. 反复操作，直到y-x=0，0就是根节点
    7. 整个数组最大的值就是根节点
  2. 将根节点与最后一个元素交换位置，（将最大元素”沉”到数组末端）
  3. 交换过后可能不再满足大顶堆的条件，所以需要将剩下的n-1个元素（数组最大长度就递减1）重新构建成大顶堆（就是不包括已经排列好的末端元素）

  4. 重复2，3步，直到排序完成

    图解

    这里以int[] a = {7, 3, 8, 5, 1, 2}为例子。

  5. 先要找到最后一个非叶子节点，数组的长度为6，那么最后一个非叶子节点就是：a.Length/2-1，也就是6/2-1=2，然后下一步就是比较该节点值和它的子树值，把最大的值放在该节点。8比2大，所以这里没有改变

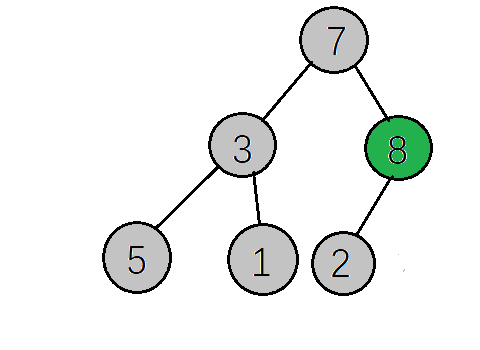
堆排序 - 图3

  1. 继续找到下一个非叶子节点（其实就是当前坐标-1就行了），把最大的值放在这个节点

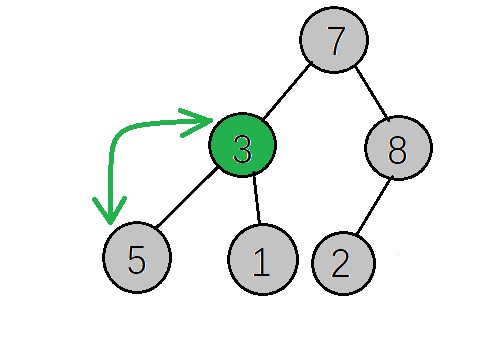
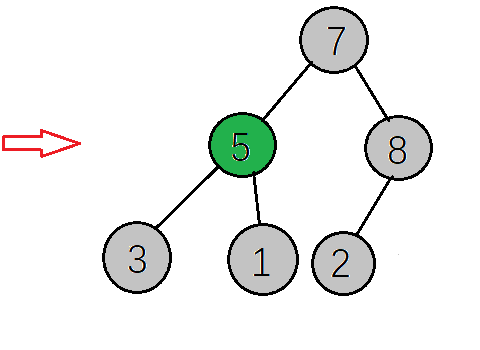
堆排序 - 图4堆排序 - 图5

  1. 继续找到下一个非叶子节点，下一个就是根节点了，同样的和左右子节点比较，把最大的值放在这个节点

堆排序 - 图6堆排序 - 图7

  1. 检查调整后的子树，是否满足大顶堆性质，如果不满足则继续调整（这里因为只将右子树的值与根节点互换，只需要检查右子树是否满足，而7>2刚好满足大顶堆的性质，就不需要调整了）
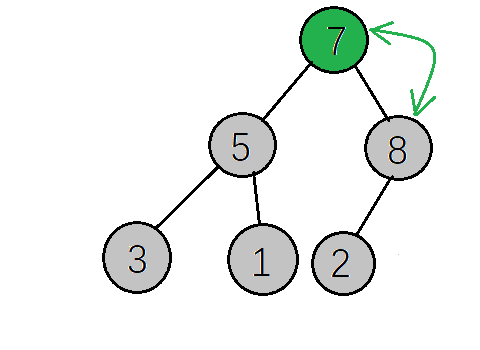
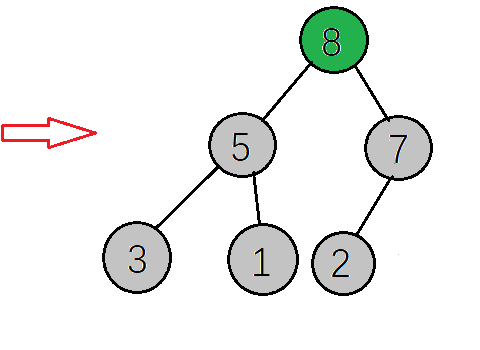
  2. 到这里大顶堆的构建就算完成了，然后下一步交换根节点（8）与最后一个元素（2）交换位置（将最大元素”沉”到数组末端），此时最大的元素就归位了，然后对剩下的5个元素重复上面的操作

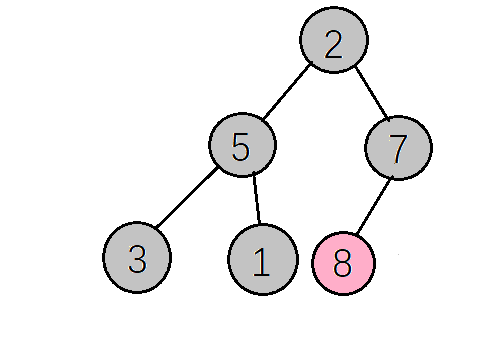
堆排序 - 图8

  1. 剩下只有5个元素，最后一个非叶子节点是5/2-1=1，同理，最大值放在该节点，因为5比3和1都大，所以不用交换

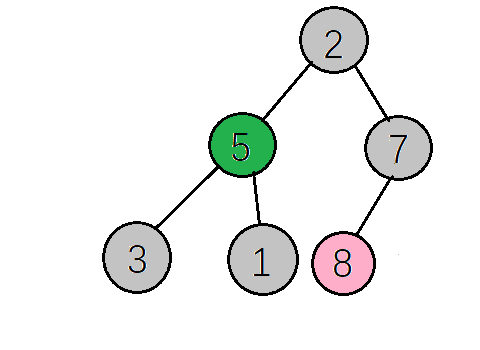
堆排序 - 图9

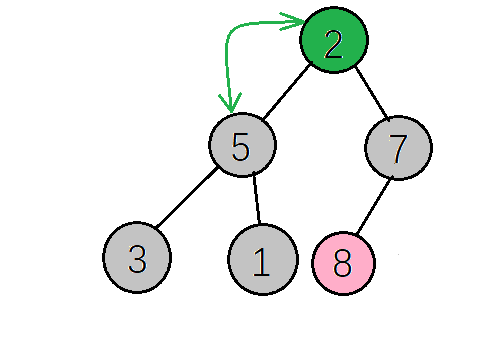
  1. 找到下一个非叶子节点，该节点的值（2）小于左子树的值（5），交换值，交换后左子树不再满足大顶堆的性质再调整左子树，左子树满足要求后再返回去看根节点，根节点的值（5）小于右子树的值（7），再次交换值

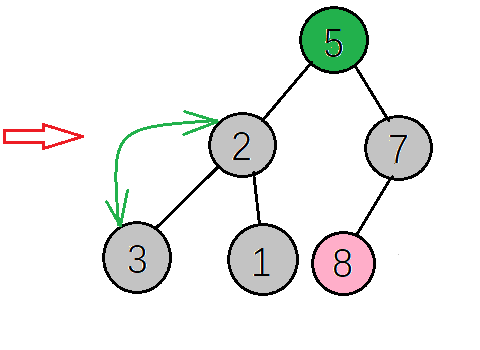
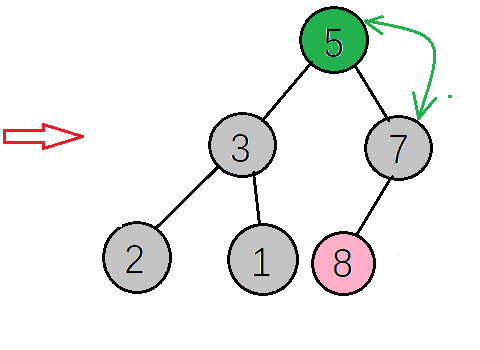
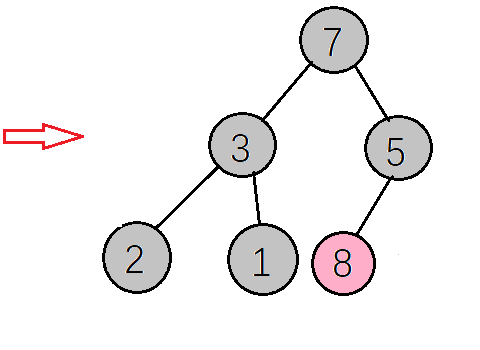
堆排序 - 图10堆排序 - 图11堆排序 - 图12堆排序 - 图13

  1. 得到新的大顶堆，如下图，再把根节点的值（7）与当前数组最后一个元素值（1）交换，重复以上操作，直到成为一个有序数组

堆排序 - 图14堆排序 - 图15

代码

  1. using System;
  2. using System.Collections.Generic;
  4. namespace ConsoleApp1
  5. {
  6.     class Program
  7.     {
  9.         static void Main(string[] args)
  10.         {
  11.             int[] array = { 4, 7, 2, 5, 3, 1, 8, 9, 6 };
  12.             HeapSort(array);
  13.             foreach(var a in array)
  14.             {
  15.                 Console.WriteLine(a);
  16.             }
  17.         }
  19.         //堆排序
  20.         static void HeapSort(int[] array)
  21.         {
  22.             //构建一个大顶堆，这是整体构建
  23.             //从最后一个非叶子节点开始，往上调整
  24.             for(int i = array.Length / 2 - 1; i >= 0; i--)
  25.             {
  26.                 adjustHeap(array, i, array.Length);
  27.             }
  29.             //整构建完成后，将堆顶的元素和末尾的元素交换，将最大元素沉到数组末尾
  30.             //完成把最大元素沉到底部的操作后，对前面的元素继续构建大顶堆，找到最大的元素，所以要排序的元素逐渐减少
  31.             //因为前面已经构建过大顶堆了，这里只是交换一下元素，可能会改变大顶堆的结构，所以再次进行一次整体调整，从根节点往下调整
  32.             for (int len = array.Length - 1; len > 0; len--)
  33.             {
  34.                 Swap(array, 0, len);
  35.                 adjustHeap(array, 0, len);
  36.             }
  37.         }
  38.         /// <summary>
  39.         /// 以当前节点i作为root节点，调整成一个大顶堆（这个大顶堆只是当前节点i作为当做root节点的树）
  40.         /// 并不是整颗树都调整成了大顶堆。最右对i不断的递减，才能逐渐调整更大的子树大顶堆
  41.         /// 直到i=0时，i作为根节点，调整的大顶堆就是完成的大顶堆
  42.         /// </summary>
  43.         /// <param name="array">带排序的数组</param>
  44.         /// <param name="i">非叶子节点在数组中的索引</param>
  45.         /// <param name="len">数组的长度（对多少个元素进行调整），len逐渐减少</param>
  46.         static void adjustHeap(int[] array,int i ,int len)
  47.         {
  48.             int temp = array[i];//先取出当前元素的值
  49.             //开始调整
  50.             //k=i*2+1是i节点的左子节点
  51.             for(int k = i * 2 + 1; k < len; k = k * 2 + 1)
  52.             {
  53.                 //这段的作用是找到左右子节点中最大的值，k指向这个值
  54.                 if (k+1 < len && array[k] < array[k + 1])//说明左子节点的值小于右子节点的值
  55.                 {
  56.                     k++;//k指向右子节点
  57.                 }
  58.                 if (array[k] > temp)//如果子节点中最大的值比父节点大，和父节点交换
  59.                 {
  60.                     array[i] = array[k];//把最大的值赋值给当前节点
  61.                     i = k;//把k赋值给i，继续循环比较
  63.                     /*在这之前k是i的子节点，i是当前节点，现在当前节点往下移动，变成了刚才变动的子节点
  64.                      * 迭代k=k*2+1，k现在又变成了i的子节点，不过ik往下移动了一层
  65.                      */
  66.                 }
  67.                 else
  68.                 {
  69.                     //本身整体从宏观来讲，整个是从最后一个非叶子节点逐渐递减，构建的大顶堆，这个for循环是从i点开始从上往下开始局部构建大顶堆
  70.                     //局部构建在整体构建之中，局部构建只是调整
  71.                     //如果局部构建发现遇到了当前节点比左右两个子节点都大的情况，说明下面的子树就不用调整了，退出局部构建
  72.                     break;
  73.                 }
  74.             }
  75.             //最终把当前点的值放到它合适的位置
  76.             array[i] = temp; 
  77.         }
  79.         //交换节点
  80.         static void Swap(int[] array,int i,int t)
  81.         {
  82.             //交换
  83.             array[i] += array[t];
  84.             array[t] = array[i] - array[t];
  85.             array[i] = array[i] - array[t];
  86.         }
  88.     }
  89. }