迪杰斯特拉算法介绍

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个结点到其他结点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止

思路

选一个节点作为起始点v
引入两个集合（S、U），S集合包含已求出的最短路径的点（以及相应的最短长度，可以再用一个集合装线路），U集合包含未求出最短路径的点，U表示起始点到这些点的距离
初始化两个集合，S集合初始时只有当前要计算的节点v，U中是除v以外的顶点
从U中找出路径最短的点加入S
更新U集合，U里面计算起始点到这些点的距离，上一个放入S的点到某一个点的距离+起始点到上一个点距离<起始点到某一个点的距离就跟更新U，详细看图解第二步
循环4，5步，直到遍历结束，得到A到其他节点的最短路径

图解
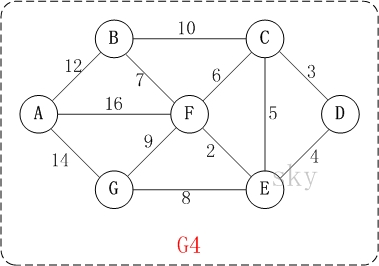
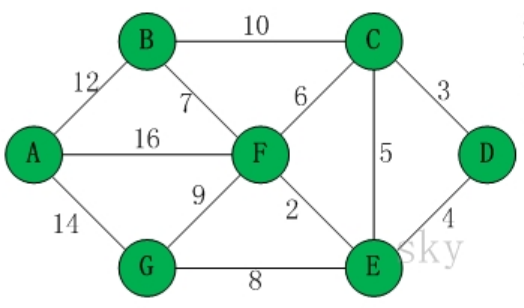
以D为起始点，第一步选取D点

S包括D[0] U包括A[x],B[x],C[3],E[4],F[x],G[x]

注：

S是已计算出最短路径的顶点的集合
U是未计算出最短路径的顶点的集合
C[3]表示顶点C到起点D的最短路径是3

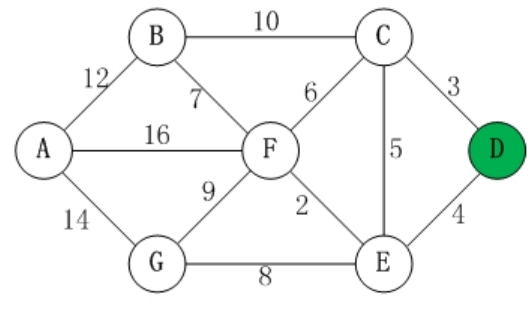
选择C，因为到C点是U中路径最短的

现在S包括D[0],C[3] U则进行调整，A[x],B[13],E[4],F[9],G[x] U表示起始点到这些点的距离。起始点到某点的距离，就是上一个放入S的点到某点的距离加上起始点到上一个放入S点的距离。例如F点，这里U里面的距离变成了9，表示上一个放入S的点C到F的距离为6，起始点D到C的距离为3，3+6=9

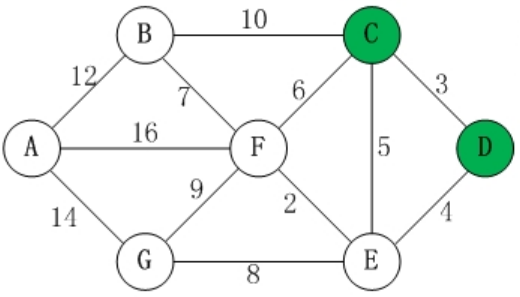
选择E，因为E[4]最短

S包括D[0],C[3],E[4] U调整为A[x],B[13],F[6],G[12]

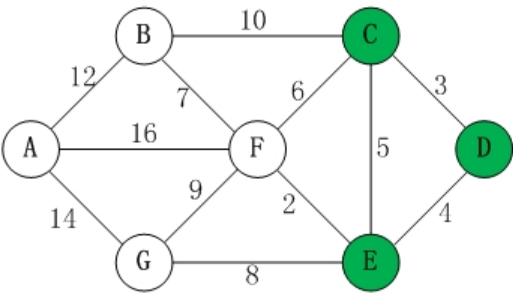
选择F[6]

S包括D[0],C[3],E[4],F[6] U调整为A[22],B[13],G[12]

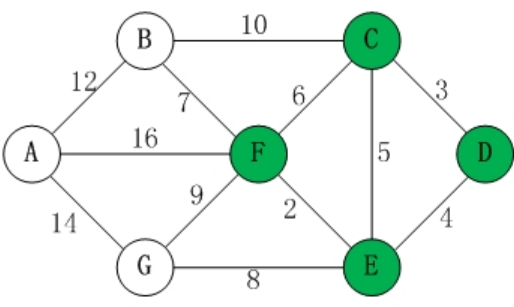
选择G[12]

S包含D[0],C[3],E[4],F[6],G[12] U调整为A[22],B[13]

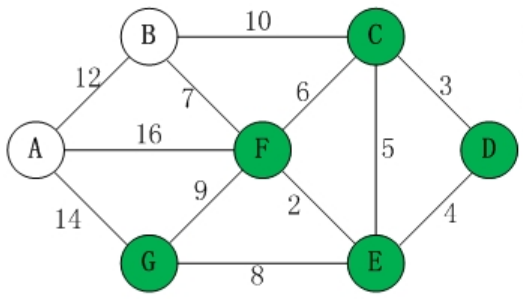
选择B[13]

S包含D[0],C[3],E[4],F[6],G[12],B[13] U调整为A[22]

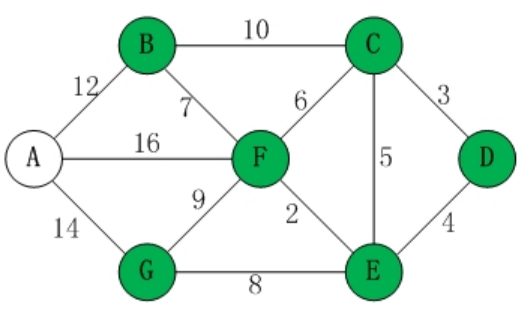
选择A[22]

S包含D[0],C[3],E[4],F[6],G[12],B[13],A[22] U没有了

代码

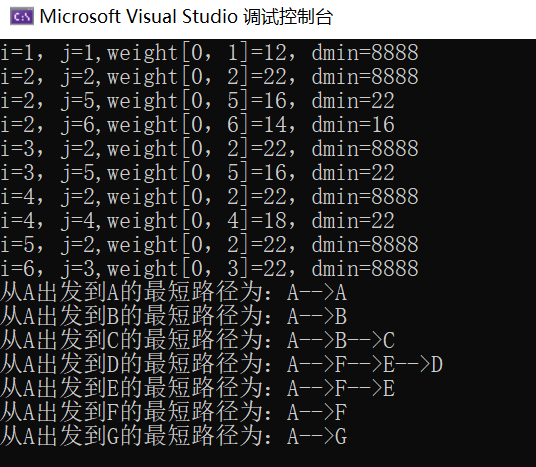
using System;
using System.Collections.Generic;
using System.Globalization;
using System.IO;
using System.Runtime.Serialization.Formatters.Binary;
using System.Text;
namespace ConsoleApp1
{
    class Program
    {
        static void Main(string[] args)
        {
            char[] vertexs = new char[] { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
            //邻接矩阵的关系使用二维数组
            //比如C和G之间不连通，就用8888来表示，权值太大就不考虑了
            int x = 8888;
            int[,] matrix = new int[,]
            {
               //A   B   C   D   E   F   G
           /*A*/{0 , 12, x , x , x , 16, 14 },
           /*B*/{12, 0 , 10, x , x , 7 , x  },
           /*C*/{x , 10, 0 , 3 , 5 , 6 , x  },
           /*D*/{x , x , 3 , 0 , 4 , x , x  },
           /*E*/{x , x , 5 , 4 , 0 , 2 , 8  },
           /*F*/{16, 7 , 6 , x , 2 , 0 , 9  },
           /*G*/{14, x , x , x , 8 , 9 , 0  }
            };
            dijkstra(matrix, vertexs, 0);
        }
        static void dijkstra(int[,] weight,char[] vertexs, int start)
        {
            int n = vertexs.Length;//顶点个数
            int[] shortPath =new int[n];//保存start点到其他顶点的最短路径
            string[] path =new string[n];//保存start点到其他顶点的最短路径的字符串表达方式，比如A->B
            for (int i = 0; i < n; i++)//字符串表达式
                path[i] = $"{vertexs[start]}-->{vertexs[i]}";
            int[] visited =new int[n];//标记当前的最短路径是否已经求出来了，1表示求出来了
            //初始化顶点，start到start的距离当前是0啊，默认start到start的距离就是已经访问过了
            shortPath[start] = 0; 
            visited[start] = 1;
            for(int i = 1; i < n; i++)//start已经访问过了，剩余要加入的顶点就是n-1
            {
                int k = -1;//选出一个距离初始顶点start最近的未标记顶点
                int dmin = 8888;//这个是最短路径，先用一个大数占位
                for(int j=0;j < n; j++)
                {
                    //选出一个距离初始顶点start最近的未标记顶点
                    if (visited[j] == 0 && weight[start, j] < dmin)
                    {
                        Console.WriteLine($"i={i}，j={j},weight[{start}，{j}]={weight[start, j]}，dmin={dmin}");
                        dmin =weight[start, j];
                        k = j;
                    }
                }
                //将新选出的顶点标记为已求出的最短路径，且到start的最短路径就是dmin
                shortPath[k] = dmin;
                visited[k] = 1;
                //以k为中间点，修正从start到未访问各点的距离  
                for(int j=0;j<n; j++)
                {
                    //核心
                    //如果 起始点到当前点的距离+当前点到某点的距离<起始点到某点的距离，则更新
                    //比如 A到G，14，加上G到E，8，等于22。A是起始点，G是当前点。而A到E的距离则为8888，因为不连通。
                    //所以AG+GB<AE,更新A到E的最短距离为22
                    if(visited[j] == 0 && weight[start, k] + weight[k, j] < weight[start, j])
                    {
                        weight[start, j] = weight[start, k] + weight[k, j];
                        path[j] = path[k] + "-->" + vertexs[j];
                    }
                }
            }
            for(int i = 0; i < n; i++)
            {
                Console.WriteLine($"从{vertexs[start]}出发到{vertexs[i]}的最短路径为：{path[i]}");
            }
        }
    }
}

编程圣经

迪杰斯特拉(Dijkstra)算法

迪杰斯特拉算法介绍

思路

图解

代码

输出