归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治策略。

思路

  1. 使用递归
  2. 每次递归都把整个序列分成两份，获得这次分解的范围，left索引到right索引，还要获得这个返回的中间索引mid
  3. 分解完成后从栈顶开始合并分解最小的基本单元
  4. 在合并的过程中定义两个指针，i和j，i指左边部分的开始索引，mid指的是中间索引，j指右边部分的开始索引，mid+1
  5. 左边，右边两个部分独立都是有序的序列，如果左边i元素＜右边j元素，就把i元素放入temp中，左边指针后移，反之，如果右边j元素<左边i元素，就把j元素放入temp中，右边指针后移
  6. 当其中一边的数据全部放入temp中，就把另一边的剩余数据顺序的放入temp中
  7. 最后在把temp中的数据拷贝到原数组的left到right这一段的位置
  8. 如上递归完成

    图解

    归并排序的动态过程
    这是归并排序的主要过程，先分解数据成最小的基本单元，然后再逐步的合并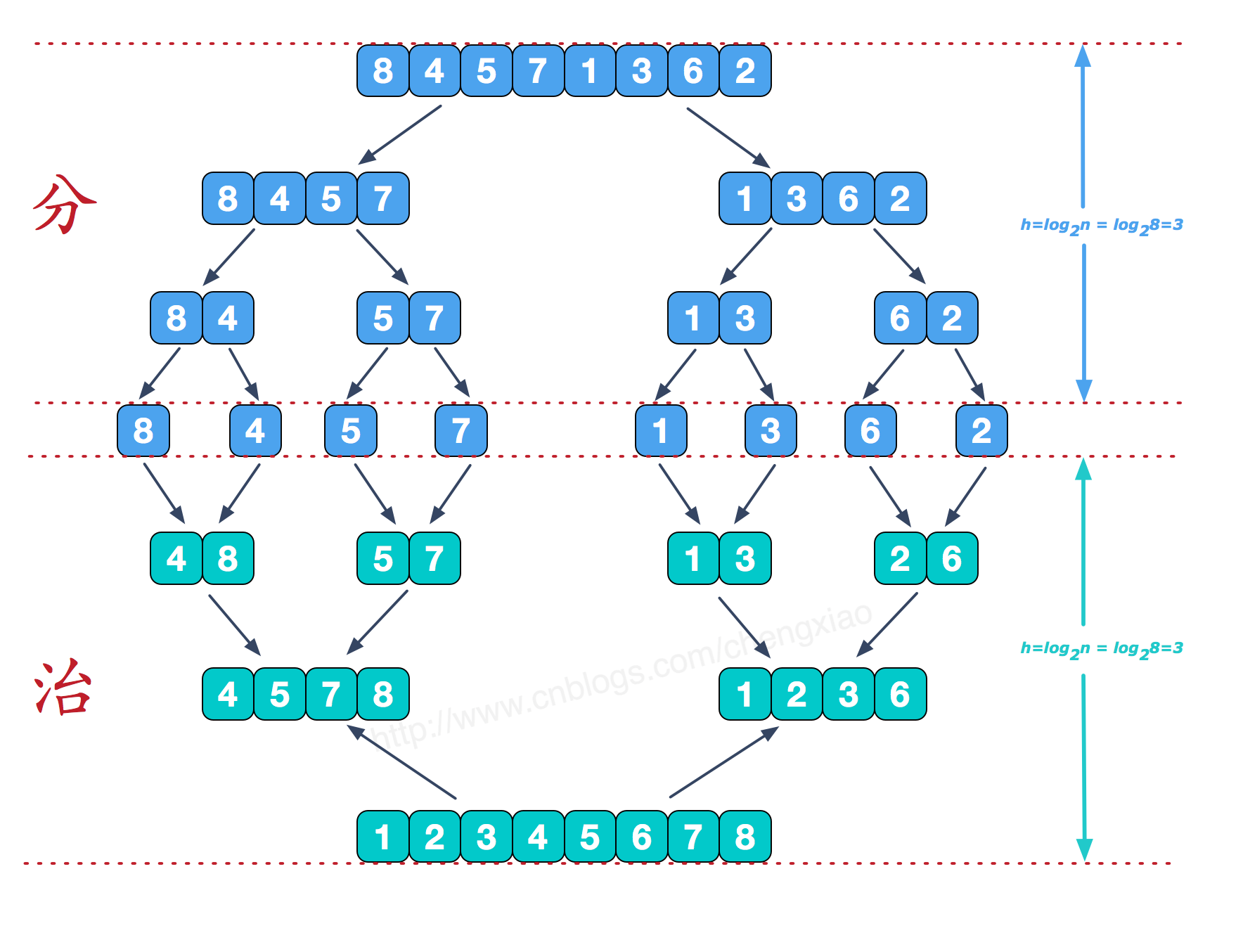
    归并排序 - 图2
    再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。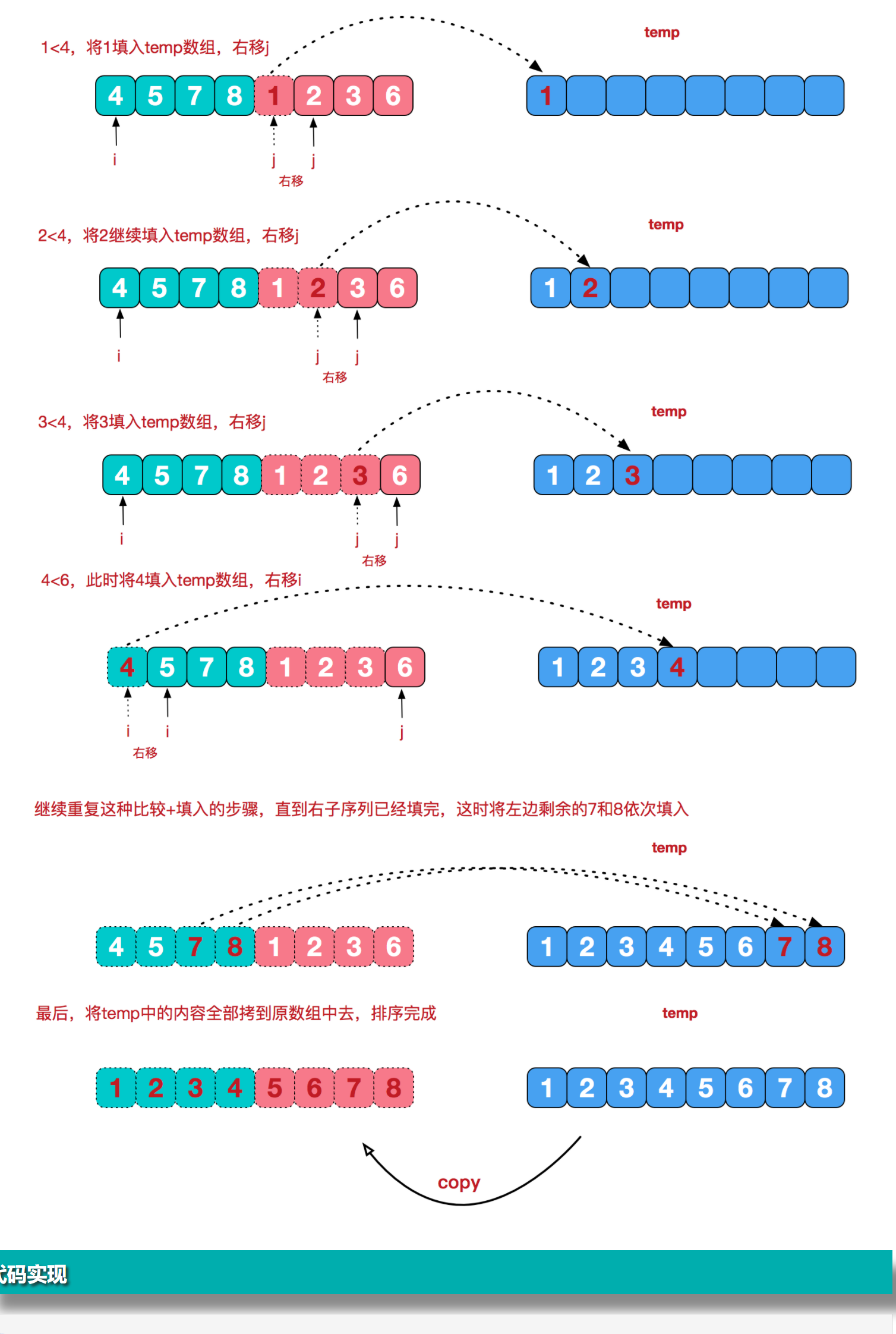
    image.png

    代码

    ```csharp using System; using System.Collections.Generic;

namespace ConsoleApp1 { class Program {

  1.     static void Main(string[] args)
  2.     {
  3.         int[] arr = new int[10] { 4, 9, 76, 43, 2, 7, 23, 54, 1, 44 };
  4.         int[] temp = new int[arr.Length];//归并排序需要一个额外的空间开销
  5.         MergeSort(arr, 0, arr.Length - 1, temp);
  6.         foreach(int a in arr)
  7.         {
  8.             Console.Write(a+" ");
  9.         }
  10.     }
  12.     static void MergeSort(int[] array,int left,int right,int[] temp)
  13.     {
  14.         if (left < right)
  15.         {
  16.             int mid = (left + right) / 2;//中间的索引
  17.             //向左递归进行分解
  18.             MergeSort(array, left, mid, temp);
  19.             //向右递归进行分解
  20.             MergeSort(array, mid + 1, right, temp);
  21.             //合并
  22.             //最后一次分解是在栈顶，合并就是栈顶传入的数据
  23.             merge(array, left, mid, right, temp);
  24.         }
  25.     }
  28.     /// <summary>
  29.     /// 合并的方法
  30.     /// </summary>
  31.     /// <param name="array">排序的原始数组</param>
  32.     /// <param name="left">左边有序序列的初始索引</param>
  33.     /// <param name="mid">中间索引</param>
  34.     /// <param name="right">右边索引</param>
  35.     /// <param name="temp">做中转的数组</param>
  36.     static void merge(int[] array,int left,int mid,int right,int[] temp)
  37.     {
  38.         int i = left;//左边有序序列的初始索引
  39.         int j = mid + 1;//右边有序序列的初始索引
  40.         int t = 0;//temp数组的当前索引
  43.         /*(一)
  44.         先把左右两边有序的数据，按规则填充到temp数组里面
  45.         知道左右两边的有序序列，有一边处理完毕为止*/
  46.         while (i <= mid && j <= right)
  47.         {
  48.             if (array[i] <= array[j])//如果左边的数小于等于右边的数，就把左边的数放在temp当前的位置，然后i和t都往后移 
  49.                 temp[t++] = array[i++];
  50.             else//反之，如上
  51.                 temp[t++] = array[j++];
  52.         }
  54.         /*(二)
  55.         把有剩余数据的一边的数据依次全部填充到temp*/
  56.         while (i <= mid)//左边的有序数列还有剩余元素，就全部填充到temp
  57.             temp[t++] = array[i++];
  58.         while (j <= right)//反之，同上
  59.             temp[t++] = array[j++];
  61.         /*(三)
  62.         将temp数组的元素拷贝到arr*/
  63.         //拷贝到的array的具体位置，就是left到right中间这一段
  64.         t = 0;
  65.         while (left <= right)
  66.             array[left++] = temp[t++];
  67.     }
  68. }

}

```