弗洛伊德算法介绍

和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名
弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径
迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。
弗洛伊德算法 VS 迪杰斯特拉算法：迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他顶点的最短路径；弗洛伊德算法中每一个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每一个顶点到其他顶点的最短路径

问题描述

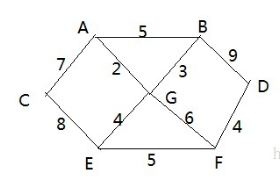
算出下图各个顶点之间的最短路径

弗洛伊德（Floyd）算法 - 图1

弗洛伊德算法的思想

弄一个二维数组，作为距离表，如下图。例如B-A的距离为5，A-D的距离为N表示不连通，N用一个很大的权值表示

遍历顶点，每一个点都作为一个中间顶点，第一次遍历，中间顶点为A

可以得到这些路径

CAB=CA+AB=7+5=12 CAG=CA+AG=7+2=9 BAG=BA+AG=5+2=7

中间点有了，又遍历全部点作为起始点（2的例子第一个C作为起点），再遍历全部点作为终点（2的例子第一个B作为终点）
三层循环
最终比较起点到中点+中点到终点的距离是否大于起点直接到终点的距离，哪个更小，就是的当前的最短路径
代码
```csharp using System; using System.Collections.Generic; using System.Globalization; using System.IO; using System.Runtime.Serialization.Formatters.Binary; using System.Text;

namespace ConsoleApp1 { class Program {

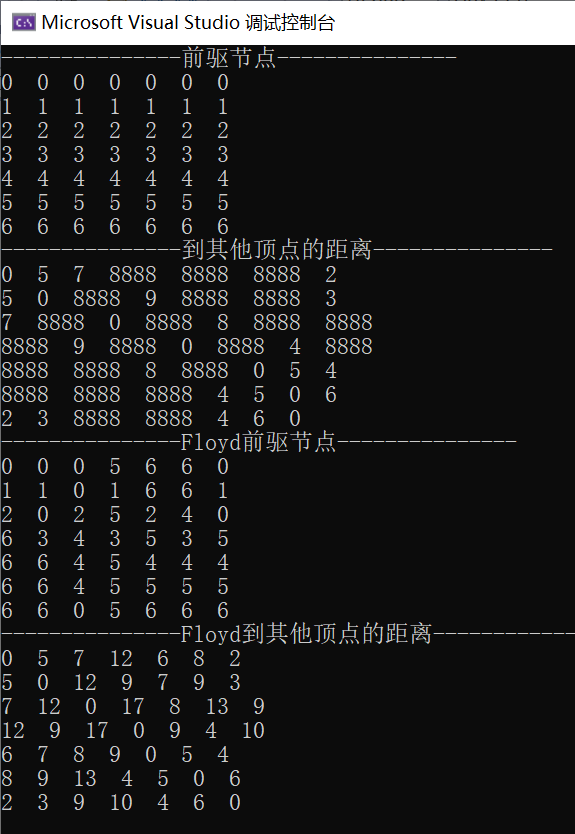
    static void Main(string[] args)
    {
        char[] vertexs = new char[] { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
        //邻接矩阵的关系使用二维数组
        //比如C和G之间不连通，就用8888来表示，权值太大就不考虑了
        int x = 8888;
        int[,] matrix = new int[,]
        {
           //A  B  C  D  E  F  G
       /*A*/{0, 5, 7, x, x, x, 2 },
       /*B*/{5, 0, x, 9, x, x, 3 },
       /*C*/{7, x, 0, x, 8, x, x },
       /*D*/{x, 9, x, 0, x, 4, x },
       /*E*/{x, x, 8, x, 0, 5, 4 },
       /*F*/{x, x, x, 4, 5, 0, 6 },
       /*G*/{2, 3, x, x, 4, 6, 0 }
        };
        Floyd(vertexs, matrix);
    }
    static void Floyd(char[] vertexs,int[,] matrix)
    {
        #region 初始化部分
        char[] vertex = vertexs;//存放顶点的数组
        int[,] dis = matrix;//保存从各个顶点出发到其他顶点的距离，最后结果也保留在该数组
        int[,] pre =new int[vertex.Length,vertex.Length];//保存到达目标顶点的前驱顶点
        //对前驱节点初始化，注意存放的是前驱顶点的下标
        for(int i = 0; i < pre.GetLength(0); i++)
            for(int j = 0; j < pre.GetLength(1); j++)
                pre[i,j] = i;
        show("前驱节点",pre);
        show("到其他顶点的距离",dis);
        #endregion
        #region 弗洛伊德算法
        int len = 0;//变量保存距离
        //对中间顶点遍历，k就是中间顶点的下标[A,B,C,D,E,F,G]
        for(int k = 0; k < vertex.Length; k++)
        {
            //从i顶点开始出发[A,B,C,D,E,F,G]
            for(int i = 0; i < vertex.Length; i++)
            {
                //到达j顶点[A,B,C,D,E,F,G]
                for (int j = 0; j < vertex.Length; j++)
                {
                    len = dis[i, k] + dis[k, j];//i顶点到k中间点的距离加上k中间点到j点的距离，就是i点到j点（中间通过k点）的距离
                    if (len < dis[i, j])//如果i到j通过k点转的距离小于i到j直达的距离，说明i-k-j是i-j更短的路径
                    {
                        dis[i, j] = len;//更新距离
                        pre[i, j] = pre[k, j];//更新前驱节点
                    }
                }
            }
        }
        show("F前驱节点", pre);
        show("F到其他顶点的距离", dis);
        #endregion
    }
    static void show(string txt,int[,] matrix)
    {
        Console.WriteLine($"---------------{txt}---------------");
        for(int i = 0; i < matrix.GetLength(0); i++)
        {
            for(int j = 0; j < matrix.GetLength(1); j++)
            {
                Console.Write(matrix[i,j]+"  ");
            }
            Console.WriteLine();
        }
    }
}

}

```

编程圣经

弗洛伊德（Floyd）算法

弗洛伊德算法介绍

问题描述

弗洛伊德算法的思想

代码

输出