图（Graph）结构是一种非线性的数据结构，图在实际生活中有很多例子，比如交通运输网，地铁网络，社交网络，计算机中的状态执行（自动机）等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。

图的构成

  1. 顶点（vertex）：图中的数据元素，如图1
  2. 边（edge）：图中连接这些顶点的线，如图1

图1
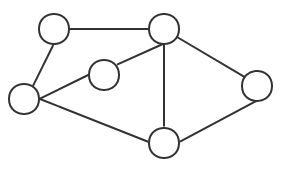
所有的顶点构成一个顶点集合，所有的边构成边的集合，一个完整的图结构就是由顶点集合和边集合组成。
图结构在数学上记为以下形式：
G=(V,E) 或者 G=(V(G),E(G))
其中 V(G)表示图结构所有顶点的集合，顶点可以用不同的数字或者字母来表示。E(G)是图结构中所有边的集合，每条边由所连接的两个顶点来表示。
图结构中顶点集合V(G)不能为空，必须包含一个顶点，而图结构边集合可以为空，表示没有边。

图的基本概念

无向图

如果一个图结构中，所有的边都没有方向性，那么这种图便称为无向图。如图2所示。由于无向图中的边没有方向性，这样我们在表示边的时候对两个顶点的顺序没有要求。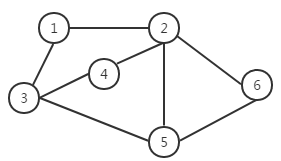
图2

路径

如图2，1到5之间的路径有如下：

  1. 1-2-5
  2. 1-3-5
  3. 1-2-4-3-5
  4. 1-3-4-2-5

    有向图

    一个图结构中，边是有方向性的，那么这种图就称为有向图，如图3所示。由于图的边有方向性，我们在表示边的时候对两个顶点的顺序就有要求。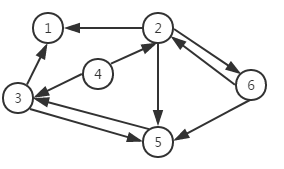
    图3
    无向图也可以理解成一个特殊的有向图，就是边互相指向对方节点，A指向B，B又指向A

    带权图

    如果一张图不含权重信息，我们就认为边与边之间没有差别。像图4这样，每条边都有一个权值，就是带权图，也叫网。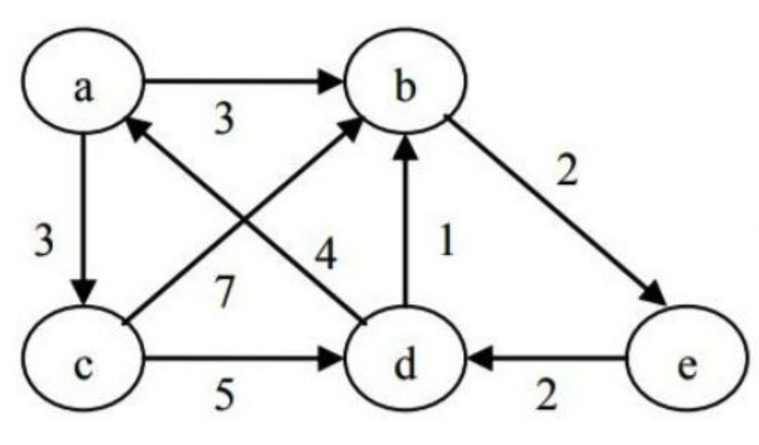
    image.png

    混合图

    一个图结构中，边同时有的是有方向性有的是无方向型的图。
    在生活中混合图这种情况比较常见，比如城市道路中有些道路是单向通行，有的是双向通行。

    顶点的度

    连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图，一个顶点V的度比较简单，其是连接该顶点的边的数量，记为D(V)。 例如，图2所示的无向图中，顶点V5的度为3。而V6的度为2。
    对于有向图要稍复杂些，根据连接顶点V的边的方向性，一个顶点的度有入度和出度之分。
  • 入度是以该顶点为端点的入边数量， 记为ID(V)。
  • 出度是以该顶点为端点的出边数量， 记为OD(V)。

这样，有向图中，一个顶点V的总度便是入度和出度之和，即D(V) = ID(V) + OD(V)。例如，图3所示的有向图中，顶点V5的入度为3,出度为1，因此，顶点V5的总度为4。

邻接顶点

邻接顶点是指图结构中一条边的两个顶点。 邻接顶点在有向图和无向图中具有不同的表示。对于无向图，邻接顶点比较简单。例如，在图2所示的无向图中，顶点V2和顶点V6互为邻接顶点，顶点V2和顶点V5互为邻接顶点等。
对于有向图要稍复杂些，根据连接顶点V的边的方向性，两个顶点分别称为起始顶点(起点或始点)和结束顶点(终点)。有向图的邻接顶点分为两类：

  • 入边邻接顶点：连接该顶点的边中的起始顶点。例如，对于组成这条边的两个顶点，V2是V6的入边邻接顶点。
  • 出边邻接顶点：连接该顶点的边中的结束顶点。例如，对于组成这条边的两个顶点，V6是V2的出边邻接顶点。

    无/有向完全图

    如果在一个无向图中， 每两个顶点之间都存在条边，那么这种图结构称为无向完全图。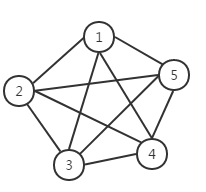
    图5
    理论上可以证明，对于一个包含M个顶点的无向完全图，其总边数为M(M-1)/2。比如图四总边数就是5（5-1）/ 2 = 10。

如果在一个有向图中，每两个顶点之间都存在方向相反的两条边，那么这种图结构称为有向完全图。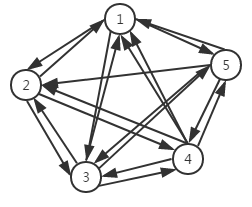
图6

图的表示方式

  1. 二维数组（邻接矩阵）

邻接矩阵是表示图形中顶点之间的相邻关系的矩阵，对于n个顶点的图而言，矩阵是row和col表示的是1….n个点。
如下图7，(0,0)=0表示0点和0点之间没有连接，(0,1)=1表示0点和1点之间可以连通。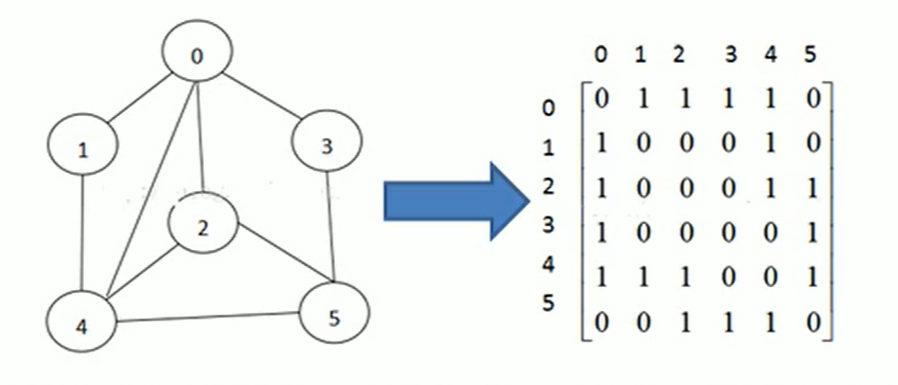
image.png

  1. 链表（邻接表）

邻接矩阵需要给每条边都分配n个边的空间，其实有很多边都是不存在，会造成空间的一定损失。
邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成。
如图8，数组里面存放链表，比如数组第0个顶点，链表为1->2->3->4，是表示1，2，3，4和0相连，并不能是说是按照顺序链接的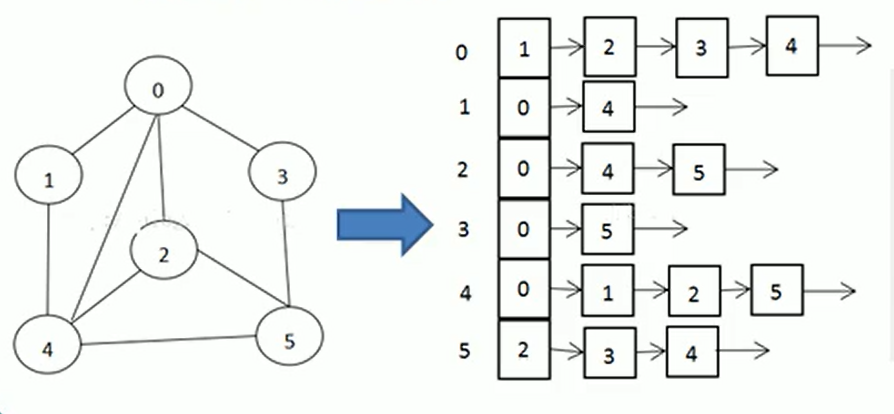
image.png

创建图代码

这里是无向图

  1. using System;
  2. using System.Collections.Generic;
  3. using System.Text;
  5. namespace ConsoleApp1
  6. {
  7.     public class Graph
  8.     {
  9.         public List<string> vertexList;//存储顶点集合
  10.         public int[,] edges;//存储图对应的邻接矩阵
  11.         public int numOfEdges;//表示边的数目
  13.         public Graph(int n)//n顶点的个数
  14.         {
  15.             //初始化矩阵和vertexList
  16.             edges = new int[n, n];
  17.             vertexList = new List<string>(n);
  18.         }
  19.         //插入顶点
  20.         public void insertVertex(string vertex)
  21.         {
  22.             vertexList.Add(vertex);
  23.         }
  25.         /// <summary>
  26.         /// 添加边
  27.         /// </summary>
  28.         /// <param name="v1">第一个顶点的下标</param>
  29.         /// <param name="v2">第二个顶点的下标</param>
  30.         /// <param name="weight">权值</param>
  31.         public void insertEdge(int v1,int v2,int weight)
  32.         {
  33.             //因为是无向表，所以v1-v2和v2-v1都需要标记
  34.             edges[v1, v2] = weight;
  35.             edges[v2, v1] = weight;
  36.             numOfEdges++;//两点之间只有一条边
  37.         }
  39.         //显示图对应的矩阵
  40.         public void showGraph()
  41.         {
  42.             for(int i = 0; i < edges.GetLength(0); i++)
  43.             {
  44.                 for(int t = 0; t < edges.GetLength(1); t++)
  45.                 {
  46.                     Console.Write(edges[i,t]+" ");
  47.                 }
  48.                 Console.WriteLine();
  49.             }
  50.         }
  52.     }
  53. }