黄金分隔点是指 把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数的近似值是0.618。

斐波那契数列：{1，1，2，3，5，8，13，21，34，55……}发现斐波那契数列的两个相邻数的比例，无限接近黄金分隔值0.618

思路

斐波那契查找的原理与二分查找和插值查找相似，仅仅改变了中间节点（mid）的位置，mid不再是中间或插值得到，而是位于黄金分割点附近
即 mid=low+F(k-1)-1

对F(k-1)-1的理解：

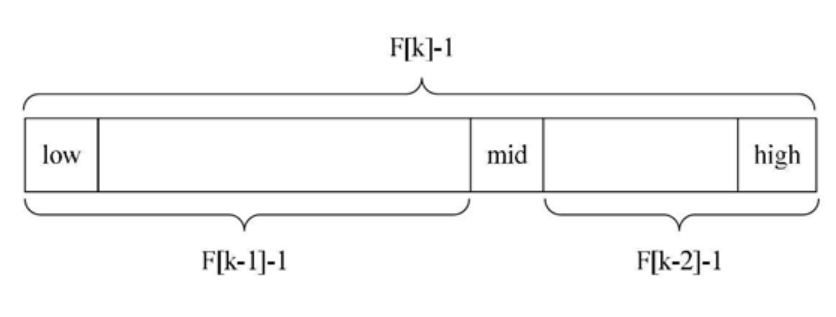
  1. 由于斐波那契数列F[k]=F[k-1]+[k-2]（当前数等于前面两个数的和）的性质，可以得到(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1

该式说明，只要数组的长度为F[k]-1，则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段。注：上面式子尾部的+1，表示数组的length，length要不最大索引+1

  1. 类似的每一段都可以用同样的方式分割

  2. 但是顺序表的长度n不一定刚好等于F[k]-1，所以需要将原来的顺序表长度增加至F[k]-1。这里的k值只要能使得F[k]-1恰好大于或者等于n即可。又下面的代码获得k值。顺序表长度增加后，新增的位置，从n+1到F[k-1]的位置，都赋为n位置的值即可。

    1. while(n>fib(k)-1)
    2.  k++;

  3. 由下图所示，从而中间位置为mid=low+F(k-1)-1

image.png

  1. 斐波那契查找还是查找的有序数列

    代码

    ```csharp using System; using System.Collections.Generic;

namespace ConsoleApp1 { class Program { static int maxFSize = 20;//斐波那契数组的大小 static void Main(string[] args) { int[] arr = new int[8] { 1, 2, 4, 6, 7, 8, 9, 13 }; Console.WriteLine(FibonacciSearch(arr,9)); } //因为mid=low+F(k-1)-1,需要使用到斐波那契数列，因此我们需要先获取到一个斐波那契数列 static int[] fib() { int[] f = new int[maxFSize]; f[0] = 1; f[1] = 1; for (int i = 2; i < maxFSize; i++) { f[i] = f[i - 1] + f[i - 2]; } return f; } //斐波那契查找 static int FibonacciSearch(int[] array,int finval) { int low = 0; int high = array.Length - 1; int k = 0;//表示斐波那契分割数值的下标 int mid = 0; int[] f = fib();//获取到斐波那契数列

  1.         //获取到斐波那契分隔数值的下标
  2.         while (high > f[k] - 1)
  3.             k++;
  5.         //f[k]对应的值不一定和array.Length相同，要保证数组的长度正好小于f[k]-1，要把数组的上限增加到f[k]
  6.         int[] temp=new int[f[k]];//声明一个新的数组，长度为f[k]
  7.         Array.Copy(array, temp, array.Length);//把原来的数组拷贝到临时数组里面去，多余的位置都是0
  8.         //实际需要使用array最后的数填充到temp里面的后面的空位上
  9.         for (int i = high + 1; i < temp.Length; i++)
  10.             temp[i] = array[high];
  12.         //使用while来循环处理，找到findval
  13.         while (low <= high)//只要这个条件满足就可以一直找
  14.         {
  15.             mid = low + f[k - 1] - 1;//找到黄金分隔点
  16.             if (finval < temp[mid])//说明要继续向mid的前面查找
  17.             {
  18.                 high = mid - 1;
  20.                 /*说明：
  21.                  *已知斐波那契数列f[k]=f[k-1]+f[k-2]
  22.                  *mid就是分隔这两个部分的，我们现在要往前继续查找，前面部分就是f[k-1]
  23.                  *又因为f[k-1]=f[k-2]+f[k-3]
  24.                  *所要找到mid就要用f[k-2]
  25.                  *再所以这里k--后，再次循环k-1，等价于k-2
  26.                  */
  27.                 k--;
  28.             }
  29.             else if (finval > temp[mid])//说明要继续向mid的后面查找
  30.             {
  31.                 low = mid + 1;
  33.                 /*说明：
  34.                  * 已知f[k]=f[k-1]+f[k-2]
  35.                  * 现在往后查找，后面部分就是f[k-2]
  36.                  * 又因为f[k-2]=f[k-3]+f[k-4]
  37.                  * 所以要找到mid需要用到f[k-3]
  38.                  * 再所以，这里k-=2后，再次循环k-1，等价于k-3
  39.                  */
  40.                 k-=2;
  41.             }
  42.             else//找到了
  43.             {
  44.                 //需要确定返回的是哪个下标
  45.                 //high是array的最大下标
  46.                 //mid是temp的黄金分隔点
  47.                 //temp后面还有一些填充的占位数据，要返回的下标一定是在集合[0,array,length-1]里面，而不是在[0,temp.length-1]里面
  48.                 if (mid <= high)
  49.                     return mid;
  50.                 else
  51.                     return high;
  52.             }
  54.         }
  56.         //没有找到就返回-1
  57.         return -1;
  58.     }
  60. }

}

```