二叉树的先中后序遍历

一、二叉树

二叉树是什么？
树中每个节点最多只能有两个子节点。

在 JS 中通常用 Object 来模拟二叉树，示例如下

const binaryTree = {
    val: 1,  // 代表当前节点的值
  left: {  // 左节点
    val: 2,
    left: null,
    right: null
  },
  right: { // 右节点
    val: 3,
    left: null,
    right: null
  },
}

二、技术实现(递归方式)

2.1 二叉树的先序遍历(preorder)

先序遍历算法口诀

• 访问根节点
• 对根节点的左子树进行先序遍历
• 对根节点的右子树进行先序遍历

示例如下图，先访问根节点1，然后访问左子树。对左子树进行先序遍历，访问根节点2；然后对根节点2的左子树再次进行先序遍历，以此类推。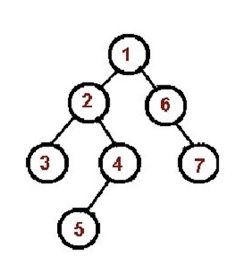

示例源码(preorder)

const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null,
    },
    right: {
      val: 5,
      left: null,
      right: null,
    },
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null,
    },
    right: {
      val: 7,
      left: null,
      right: null,
    },
  }
}
const preorder = (root) => {
  if (root == null) return;
  console.log(root.val)   // 第一步：访问根节点
  preorder(root.left)     // 第二步：访问左子树(递归访问)
  preorder(root.right)    // 第三步：访问右子树(递归访问)
}
preorder(bt) // 1 2 4 5 3 6 7

2.2 二叉树的中序遍历(inorder)

中序遍历算法口诀

• 对根节点的左子树进行中序遍历
• 访问根节点
• 对根节点的右子树进行中序遍历

示例如下图，针对根节点5，会先访问左子树，即以2为根节点的左子树。然后针对以2为根节点的树，会先访问左子树，即子节点1，然后访问根节点2，然后访问以4为根节点的右子树。针对以4为根节点的树，会先访问左子树3节点，然后访问根节点4，以此类推。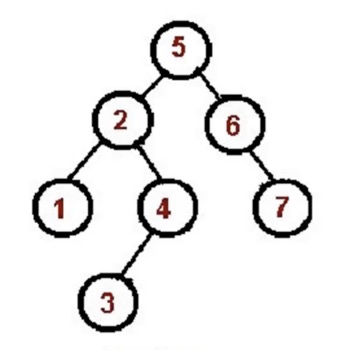

const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null,
    },
    right: {
      val: 5,
      left: null,
      right: null,
    },
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null,
    },
    right: {
      val: 7,
      left: null,
      right: null,
    },
  }
}
const inorder = (root) => {
  if (root == null) return;
  inorder(root.left)     // 第一步：访问左子树(递归访问)
  console.log(root.val)  // 第二步：访问根节点
  inorder(root.right)    // 第三步：访问右子树(递归访问)
}
inorder(bt)

2.3 二叉树的后序遍历(postorder)

后序遍历算法口诀(左->右->根)

• 对根节点的左子树进行后序遍历
• 对根节点的右子树进行后序遍历
• 访问根节点

示例如下图，针对根节点7，会先访问左子树，即以4为根节点的左子树。然后针对以4为根节点的树，会先访问左子树，即子节点1，然后访问以3为根节点的右子树。针对以3为根节点的树，会先访问左子树2节点，然后访问根节点3，以此类推。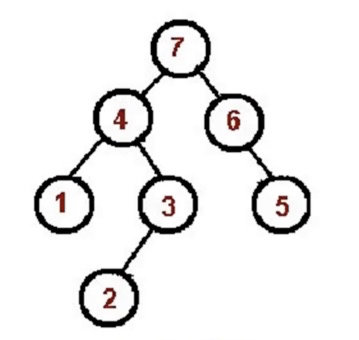

const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null,
    },
    right: {
      val: 5,
      left: null,
      right: null,
    },
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null,
    },
    right: {
      val: 7,
      left: null,
      right: null,
    },
  }
}
const postorder = (root) => {
  if (root == null) return;
  postorder(root.left)     // 第一步：访问左子树(递归访问)
  postorder(root.right)    // 第二步：访问右子树(递归访问)
  console.log(root.val)    // 第三步：访问根节点
}
postorder(bt)

三、技术实现(非递归方式)

基于递归方式实现的二叉树先中后序往往太简单了，面试官不屑于考查这类题。为了筛选出高水平的候选人，往往会要求写出非递归版的二叉树先中后序遍历。

3.1 二叉树的先序遍历(preorder)

可基于函数调用栈来实现这一思路，用栈来模拟递归的过程。

const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null,
    },
    right: {
      val: 5,
      left: null,
      right: null,
    },
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null,
    },
    right: {
      val: 7,
      left: null,
      right: null,
    },
  }
}
const preorder = (root) => {
  if (root == null) return;
  const stack = [root]  // 代表当前栈里面要访问的是根节点
  while (stack.length) {
    // 第一步：访问根节点的值
    const current = stack.pop()
    console.log(current.val)
    // 由于栈是先进后出结构，故需在左子树之前先推右子树。
    if (current.right) stack.push(current.right) // 第三步：右子树存在，将其推到栈中。
    if (current.left) stack.push(current.left)   // 第二步：左子树存在，将其推到栈中
  }
}
preorder(bt)  // 1 2 4 5 3 6 7

3.2 二叉树的中序遍历(inorder)

可基于函数调用栈和指针实现这一思路，用栈来模拟递归的过程。

const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null,
    },
    right: {
      val: 5,
      left: null,
      right: null,
    },
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null,
    },
    right: {
      val: 7,
      left: null,
      right: null,
    },
  }
}
const inorder = (root) => {
  if (root == null) return;
  const stack = []
  // 对于中序遍历来说，要先把所有的左子树丢到栈中，此处借助指针
  let p = root
  while (stack.length || p) {
    while (p) {
      stack.push(p) // 每遍历一个将其推到栈里面
      p = p.left // 不断遍历左子树
    }
    // 访问最近的节点
    const current = stack.pop()
    console.log(current.val)
    p = current.right // 访问右节点
  }
}
inorder(bt)

3.3 二叉树的后序遍历(postorder)

实现后序遍历有个技巧，将“左->右->根”倒过来，变成“根 -> 右 -> 左” ，这个时候跟先序遍历就没有太多差别。具体思路如下：

• 先将先序遍历的访问操作变成入栈操作；
• 利用栈的后进先出特性，把子节点全部逆序输出出来再访问，从而实现后序遍历 ```javascript const bt = { val: 1, left: { val: 2, left: {

  val: 4,
  left: null,
  right: null,

  }, right: {

  val: 5,
  left: null,
  right: null,
  

  }, }, right: { val: 3, left: {

  val: 6,
  left: null,
  right: null,
  

  }, right: {

  val: 7,
  left: null,
  right: null,
  

  }, } }

const postorder = (root) => { if (root == null) return;

const stack = [root] // 实现先序遍历 const outputStack = [] // 将先序遍历的访问操作改成入栈操作

// 变形版的先序遍历，根 -> 右 -> 左 while (stack.length) { // 第一步：访问根节点的值 const current = stack.pop()

outputStack.push(current)

// 由于栈是先进后出结构，故需在右子树之前先推左子树。
if (current.left) stack.push(current.left)   // 第三步：左子树存在，将其推到栈中
if (current.right) stack.push(current.right) // 第二步：右子树存在，将其推到栈中。

}

// 然后进行逆序输出 while (outputStack.length) { const node = outputStack.pop() console.log(node.val) } }

postorder(bt) ``` 利用两个栈来实现二叉树的后序遍历。