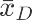- 第四节 利用ABTest寻求电商流量分配的最优解
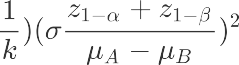
#读取SQL数据con=pymysql.connect(host=’127.0.0.1’,port=3306,user=’root’,passwd=’123456’,db=’A BTest’,use_unicode=True, charset=”utf8”)
data=pd.read_sql(“select * from ABTest”,con=con) data.head()
# 根据常规默认值确定α ,β,K 值 α = 0.05, β = 0.2 ,K = 1 (组件样本均衡) alpha = 0.05
beta = 0.2
k =1">引用包
import pandas as pd import numpy as np
import matplotlib.pyplot as plt from scipy import stats
import pymysql import warnings
warnings.filterwarnings(‘ignore’) plt.rcParams[‘font.family’]=’SimHei’ plt.rcParams[‘axes.unicode_minus’]= False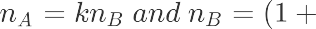
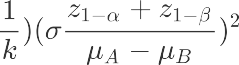
#读取SQL数据con=pymysql.connect(host=’127.0.0.1’,port=3306,user=’root’,passwd=’123456’,db=’A BTest’,use_unicode=True, charset=”utf8”)
data=pd.read_sql(“select * from ABTest”,con=con) data.head()
# 根据常规默认值确定α ,β,K 值 α = 0.05, β = 0.2 ,K = 1 (组件样本均衡) alpha = 0.05
beta = 0.2
k =1- 抽取A类店铺一天数据
df = data.loc[(data.riqi==’2020-05-14’) & (data.店铺类型==”A”),[“组”,”下单量”]] df.head() - 统计对照组(D组)的标准差
df_std = data.loc[data.店铺类型==”A”,[“组”,”riqi”,”下单量”]]
std = df_std[df_std.组==”D”].groupby(“riqi”)[“下单量”].mean().std() std - 为让A类店铺无明显感知利润下降,我们设置A类店铺下降阈值为2个标准差muzhicha =std *2
muzhicha - 寻找最优组与最优质值
best_group_name = df.groupby(group_col) [value_col].mean().sort_values(ascending=False).index.tolist()[0]
best_group_values = df[df[group_col] == best_group_name][value_col] # 最优组
的values
# 去除最优组的组名
group_names = list(set(df[group_col].unique().tolist()) - set(best_group_name))
# 初始化返回数据
pdf = pd.DataFrame(columns=[group_col,’mean’, ‘pvalue’, ‘ptype’]) # 计算差异性
for group_name in group_names:
group_values = df[df[group_col] == group_name][value_col] - 第五节 总结与拓展
第四节 利用ABTest寻求电商流量分配的最优解
实验方案:
在下单推荐页设置固定中小店铺展示位置,通过对比3个固定展示位、6个、9个的区别,探究最优展示 位个数。




选择实验主要指标
二类指标的确定
目标:提升中小店铺在下单推荐页的下单量30%
由于总量无法作为假设检验统计量,通过总下单量 = 人数 * 人均下单量,将统计量指标定为人均中小店铺下单量。此时就能确定二类指标:
二类指标:C类店铺人均下单量上升 30%
一类指标的确定
在下单推荐页将一部分流量固定分配给中小店铺,那大店铺的流量肯定会受到损失。从前期的分析来 看,近一月的大店铺的流量仅有3%来源与下单推荐页,贡献成单量仅占2%。所以即使页面完全展示中小店铺结果,大店铺的整体流量影响能控制在3%内,大店铺的成单影响能控制在2%内。
一类指标:A类店铺人均下单量下降在两个标准差以内
设计原假设与备择假设
一类指标: H1 : 对照组人均下单量 - 实验组人均下单量 < 2 实验前人均下单量标准差
H0 : 对照组人均下单量 - 实验组人均下单量 >= 2 实验前人均下单量标准差
二类指标 : H1: 实验组人均下单量 - 对照组人均下单量 > 30%对照组人均下单量H0: 实验组人均下单量 - 对照组人均下单量 <= 30%对照组人均下单量
计算分组样本量
选择两个总体均值之差计算公式 ,从假设上看一类二类指标都为单侧检验,但由于我们现在还没有做抽样,所以我们不知道实验组的σ^2,我们在这里假定AB组σ^2相等,带入后我们公式变为。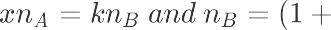
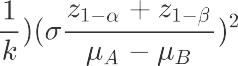
python实现代码如下
引用包
import pandas as pd import numpy as np
import matplotlib.pyplot as plt from scipy import stats
import pymysql import warnings
warnings.filterwarnings(‘ignore’) plt.rcParams[‘font.family’]=’SimHei’ plt.rcParams[‘axes.unicode_minus’]= False
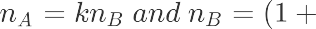
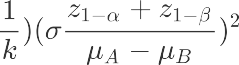
#读取SQL数据con=pymysql.connect(host=’127.0.0.1’,port=3306,user=’root’,passwd=’123456’,db=’A BTest’,use_unicode=True, charset=”utf8”)
data=pd.read_sql(“select * from ABTest”,con=con) data.head()
# 根据常规默认值确定α ,β,K 值 α = 0.05, β = 0.2 ,K = 1 (组件样本均衡) alpha = 0.05
beta = 0.2
k =1
求  和
和 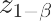
z_alpha = stats.norm.ppf(1-alpha) z_beta = stats.norm.ppf(1-beta) print(z_alpha,z_beta)
1.959963984540054 0.8416212335729143
求
df_C = data.loc[(data.组==’D’) & (data.店铺类型==”C”),[“riqi”,”下单量”]] sigema = df_C[“下单量”].std()
sigema 0.4560376923365469
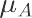
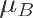 求二类目标提升值 :
求二类目标提升值 :
mean = df_C.groupby(“riqi”)[“下单量”].mean().mean()*0.3 mean
0.031065555555555555
yangbenlang = (1+1/k)np.power(sigema(z_alpha+z_beta)/mean,2) #随着miua-miub差值愈大所需要的样本量愈小
yangbenlang
3382.835657318574
求
df_A = data.loc[(data.组==’D’) & (data.店铺类型==”A”),[“riqi”,”下单量”]] sigema = df_A[“下单量”].std()
sigema
1.90306885529098
求一类目标降低值: 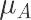
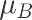
mean = df_A.groupby(“riqi”)[“下单量”].mean().std()*2 mean
0.19578164968724276
yangbenlang = (1+1/k)np.power(sigema(z_alpha+z_beta)/mean,2) #随着miua-miub差值愈大所需要的样本量愈小
yangbenlang
1483.2102112443183
日活:1000w
平均每组0.1%流量。
检验策略选择
由于我们明确了一类指标的下降阈值和二类指标的上升目标,所以都使用单侧检验。
设计分组策略
A组:下单推荐页前12个推荐,9个C类店铺商品B组:下单推荐页前12个推荐,6个C类店铺商品C组:下单推荐页前12个推荐,3个C类店铺商品D组:不干预(对照组)
实验结论分析
import pandas as pd import numpy as np
import matplotlib.pyplot as plt from scipy import stats
import pymysql import warnings
warnings.filterwarnings(‘ignore’) plt.rcParams[‘font.family’]=’SimHei’ plt.rcParams[‘axes.unicode_minus’]= False
con=pymysql.connect(host=’127.0.0.1’,port=3306,user=’root’,passwd=’123456’,db=’A BTest’,use_unicode=True, charset=”utf8”)
data=pd.read_sql(“select * from ABTest”,con=con) data.head()
一类指标假设检验
抽取A类店铺一天数据
df = data.loc[(data.riqi==’2020-05-14’) & (data.店铺类型==”A”),[“组”,”下单量”]] df.head()
df.groupby(“组”)[“下单量”].count() #查看每组样本量
df = df[df.组 != “C”] #C组样本悬殊故C组不参与检验df.组.unique()
df.groupby([“组”])[“下单量”].mean()
统计对照组(D组)的标准差
df_std = data.loc[data.店铺类型==”A”,[“组”,”riqi”,”下单量”]]
std = df_std[df_std.组==”D”].groupby(“riqi”)[“下单量”].mean().std() std
为让A类店铺无明显感知利润下降,我们设置A类店铺下降阈值为2个标准差muzhicha =std *2
muzhicha
0.19578164968724276
求AD组
alpha =0.05
# H0: μD - μA >=0.195 H1: μD - μA <0.195
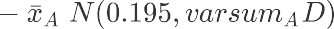 计算dif_AD 在相应的分布的概率p
计算dif_AD 在相应的分布的概率p
计算统计量 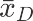
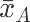
求 
dif_AD = df.下单量[df.组==”D”].mean() - df.下单量[df.组==”A”].mean() dif_AD
0.6861399544246107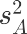
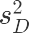
varsum_AD = df.下单量[df.组==”A”].var()/df.下单量[df.组==”A”].count() + df.下单量[df.组==”D”].var()/df.下单量[df.组==”D”].count()
varsum_AD
0.0004817503857263059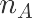
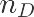
p_A = stats.norm.cdf(dif_AD,loc=muzhicha,scale=np.sqrt(varsum_AD)) # norm.dist p_A
求BD组
dif_BD = df.下单量[df.组==”D”].mean() - df.下单量[df.组==”B”].mean() varsum_BD = df.下单量[df.组==”D”].var()/df.下单量[df.组==”D”].count() + df.下单量[df.组==”B”].var()/df.下单量[df.组==”B”].count()
# dif ~ N(0.1, varsum)
# 计算dif 在相应的分布的概率p
p_B = stats.norm.cdf(dif_BD,loc=muzhicha,scale=np.sqrt(varsum_BD)) p_B
if (p_A < alpha) & ( p_B < alpha): if dif_A
else:
print(“B策略对A类店铺影响小”) elif p_A < alpha:
print(“A策略对A类店铺影响小与阈值” + str(muzhicha)) elif p_B < alpha:
print(“B策略对A类店铺影响小与阈值” + str(muzhicha)) else:
print(“A.B策略对A类店铺影响超过阈值” + str(muzhicha))
B策略对A类店铺影响小与阈值0.19578164968724276
二类指标假设检验
df_C = data.loc[(data.riqi==’2020-05-14’) & (data.店铺类型==”C”),[“组”,”下单量”]] df_C.head()
df_C.groupby([“组”])[“下单量”].count()
#去除C组
df_C = df_C[df_C. 组 != “C”] df_C.groupby([“组”])[“下单量”].mean()
计算提升值 $\mu_A - \mu_B$
tisheng = data[(data.组==’D’) & (data.店铺类型==”C”)].groupby(“riqi”)[“下单量”].mean().mean()*0.3
tisheng
0.031065555555555555
ABTest封装函数
def abtest(df: pd.DataFrame, alpha=0.05, group_col: str = None, value_col: str = None):
‘’’
:param df: 被分析DateFrame对象
:param alpha: 临界值
:param group_col: 组列的名字,默认为df的第一列
:param value_col: 值列的名字,默认为df的第2列
:return:best_group_name,pdf best_group_name:最优组pdf:最优组与其他组的差异性
‘’’
# 列名
if not group_col:
group_col = df.columns[0] if not value_col:
value_col = df.columns[1]
寻找最优组与最优质值
best_group_name = df.groupby(group_col) [value_col].mean().sort_values(ascending=False).index.tolist()[0]
best_group_values = df[df[group_col] == best_group_name][value_col] # 最优组
的values
# 去除最优组的组名
group_names = list(set(df[group_col].unique().tolist()) - set(best_group_name))
# 初始化返回数据
pdf = pd.DataFrame(columns=[group_col,’mean’, ‘pvalue’, ‘ptype’]) # 计算差异性
for group_name in group_names:
group_values = df[df[group_col] == group_name][value_col]
dif = best_group_values.mean() - group_values.mean()
var = best_group_values.var()/best_group_values.count() + group_values.var()/group_values.count()
pvalue =1-stats.norm.cdf(dif,loc=tisheng,scale=np.sqrt(var))
if pvalue >= alpha: ptype = “无显著差异”
else:
ptype = “有显著差异” # 添加数据
pdf.loc[pdf.shape[0]] = {group_col: group_name,’mean’:group_values.mean(), ‘pvalue’: pvalue, ‘ptype’: ptype}
return best_group_name,best_group_values.mean(), pdf
abtest(df_C)
(‘B’, 0.4697,
组 mean
0 A 0.0064
1 D 0.1318
pvalue ptype
0.0 有显著差异
0.0 有显著差异)
实验结论与后续决策
一类指标评估:B策略的一类指标下降幅度在两个标准差内,符合要求;
二类指标评估:B策略的二类指标最优,同时上升幅度显著大于30%,符合要求; 决策:考虑推全B策略。
为了避免我们的取的那天数据是一个异常值,可以多用几天的数据来做检验。
第五节 总结与拓展
如何做一个好的ABTest
1、确定对照组和实验组,最好是做单变量的实验,一次只改变一个变量。
2、分流时尽量排除混杂因素,一般情况下采用随机分流即可。如果随机分流无法保证样本分布于总体分 布一致。建议采用手动的分层随机分流。
3、检查流量是否达到最小样本量要求,达不到要求则没法进行后续的分析,实验结果不可信。
4、准确收集用户行为数据,这就要求埋点必须正确。
ABTest的局限
细小改变与重大改变的博弈
- 数据驱动与业务灵感的平衡