第二节 学习企业ABTest业务流程

会假设检验就够了吗？

会做假设检验只相当于会分析ABTest的结果

我们教材上的假设检验题：

题目给我们的挑战：

而我们实际遇到的需要ABTest的业务：

实际业务的ABTest流程

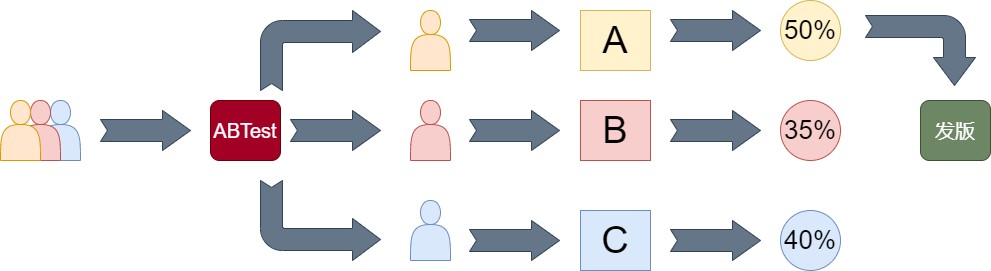
人员配置：数据分析师（1人） 项目周期：1~2周
项目流程：

从假设检验到ABTest

普通逻辑

If A then NOT B;
普通逻辑会有逆反命题：
B
then NOT A;

假设检验逻辑：

if A then probably β NOT B;
这个时候，如果我们知道同条件下的各β，我们就能判断各先决条件的可信度。 同理，我们也可以有逆反命题：
B
then probably NOT A;

这里，我们就能推导出假设检验的基本逻辑：
当你想证明一个事件 A 不成立的时候。你可以先找到一件当事件 A 成立时很大程度不会发生的事件 B
。这时当你发现事件 B 发生的时候，你就有很大把握证明A不成立。
所以我们只需要证明“事件 A 成立时很大程度不会发生的事件 B”，我们就能让以上的逻辑成立：

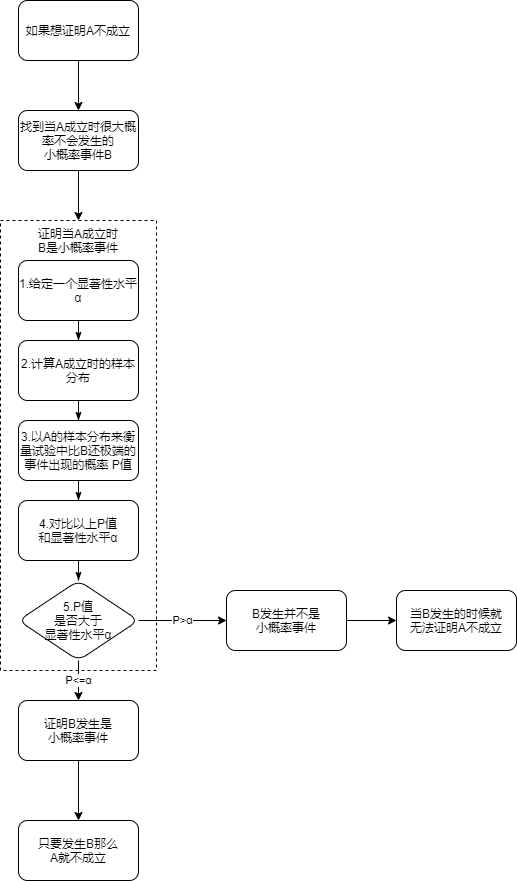
假设检验关键步骤

让我们用一组最简单的硬币实验来说明这个流程：
假设我们是一家游戏机中心，我们有一款投币游戏机，如果投进去的硬币足够均匀，那么投的玩家就特 别不容易赢。所以我们对硬币生产厂的生产的硬币要求很高。

为了检验硬币是否是均匀的，我们甚至研发了一款投硬币机，可以同时快速地投100枚硬币，并记录投 币结果，然后依据一组投递结果，筛选出合格的硬币。但是现在离研发成功还差最后一步，就是给机器 设定硬币合格的阈值：
出现什么情况我们会判断硬币是不均匀的？

我们需要一组完全对立的假设

在假设检验的基本逻辑中，我们把想证明的结论写成备择假设，把想拒绝的结论写成原假设。
在我们的假设检验逻辑中，A成立一般会被我们选为原假设 H0；而A不成立，一般会被我们选择为备择假设 H1（国外一般使用Ha)。
H0: A事件成立 A
H1: A事件不成立 NOT A
我们主要做的事情：是通过证明B是一个小概率事件，从而证明备择假设H1成立。那我们抛硬币实验的假设就可以设置为如下：
H0：硬币是均匀的 （A）
H1：硬币是不均匀的 （NOT A）

我们需要一个小概率发生的极端事件B

比如我们找了几个负责研发投硬币机的同事，让他们给出当硬币是均匀的时候基本不会发生的极端事 件：
B1:投100次硬币有90次都是正面B2:投100次硬币有54次都是正面B3:投100次硬币有60次都是正面B4:投100次硬币有58次都是正面B5:投100次硬币有63次都是正面

给我们的“大概率”一个阈值

显著性水平 0.05

计算A成立时的分布和样本统计量分布

比如我们的投硬币实验，假设我们的硬币是均匀的，那我们的总体分布就符合p=0.5的二项分布。那我们知道总体分布后，我们还需要知道样本符合什么分布。
假设我们做一组10次投币的实验
这时候我们会出现多少种可能的结果？ 我们用无顺序的组合数公式：

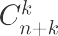
算式可以算出来。
而每种结果，对应的就是我们的样本，每个样本出现概率的分布，就是我们的样本分布。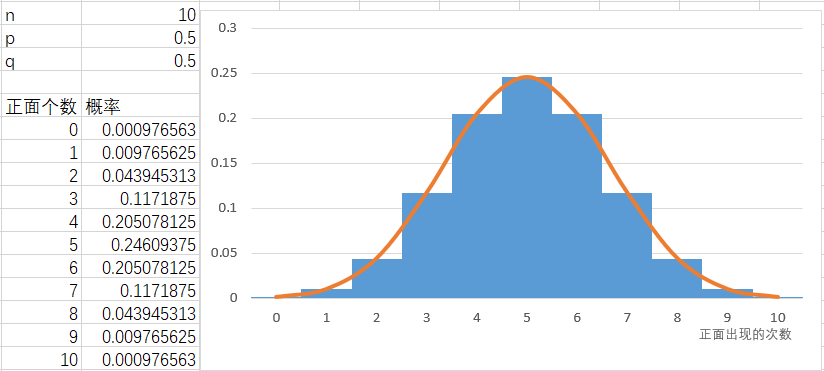

这个分布就是样本分布。

那回到实验做一组100次投币
对于二项分布的样本分布，我们一般描述为：
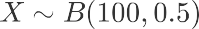其中n为重复次数，p为出现其中一项的概率。在我们这里对于二项分布：

1. 均值：

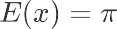
1. 方差：

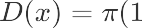
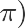
那扩大到实验做k次，每次实验投硬币100次，这时候，我们直接带入n和p用原来的算式来计算概率分布。

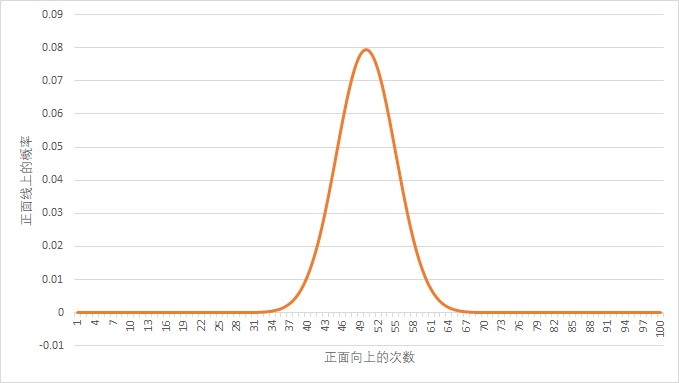
由于二项分布是某事发生概率的分布，我们将正面向上次数转化为一次实验正面线上的概率，那么他的 样本分布就变成：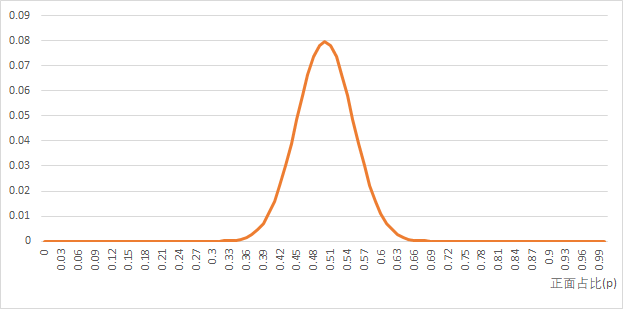

这时，我们的总体期望为：π = 0.5；总体方差为：π (1 - π) = 0.25
我们利用中心极限定理：从均值为μ、方差为σ^2的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值 xbar 的抽样分布近似服从均值为μ、方差为σ^2/n的正态分布。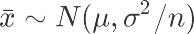

这时候，我们的样本比例的分布同样可以适用于中心极限定理，其样本比例的期望π可以直接套用其公 式中的均值μ，套用公式可得：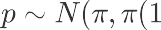

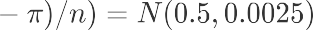
对比B发生时的统计量位置，计算更极端事件的发生概率 P值

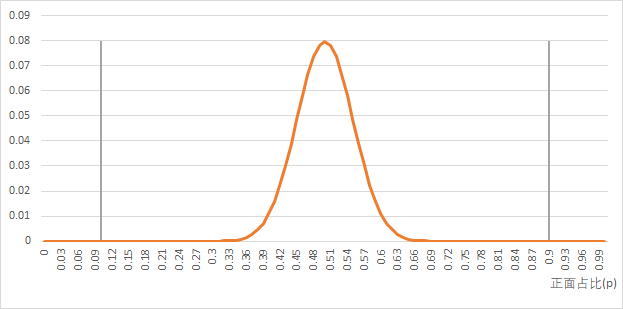
比“投100次硬币有90次都是正面”（B1事件）更极端的事件有什么？ 比如“91 次正面，9 次反面”、“91 次反面，9 次正面”……
转化为比例则为：“正面比例为0.91”，“正面比例为0.09”……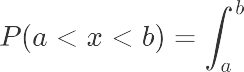
P 值就是比所得到的样本观察结果更极端的结果出现的概率。我们计算的公式一般是这个：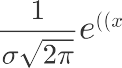

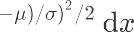
由于计算复杂，我们可以直接借助于统计工具计算： 使用Excel的函数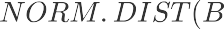
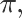发生的比例 样本比例的期望 样本 比例的标准差 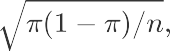是否是累计概率

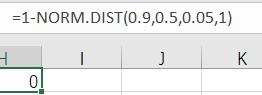求正态分布的概率：
求得P值为0（实际应为1.2442E-15，但是这个数据过小，Excel计算不出来）。

2.3.6.对比P值和显著性水平的大小，证明在A事件发生的条件下，B事件是小概率事件

由于P值小于显著水平α，这时我们可以说B1事件是极小概率概率事件。我们就能利用之前的逻辑：
B
then probably NOT A;
所以我们有足够的理由拒绝原假设，接受备择假设。

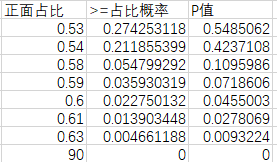之后我们将B2~B5的情况都计算一遍，

可以发现“投100次硬币60次都是正面”的时候，P值刚好大于显著性水平。所以有的时候我们直接使用显著性水平计算一个统计量的阈值。
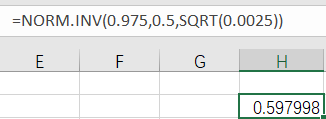
使用Excel的函数NORM.INV()，可以求出显著性水平对应的阈值：

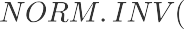
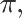
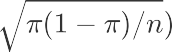阈值对 应位置 样本比例的期望 样 本比例的标准差

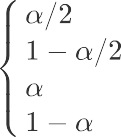其中， 阈值对应 位置
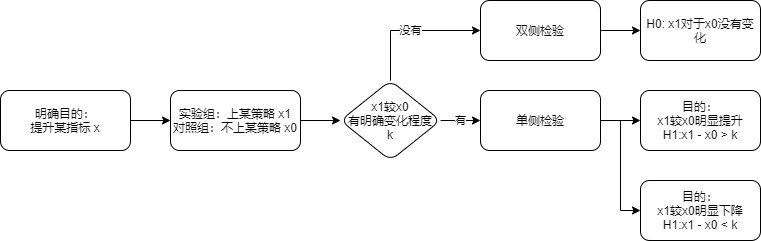
双侧检验左侧拒绝域双侧检验右侧拒绝域单侧检验左侧拒绝域单侧检验右侧拒绝域

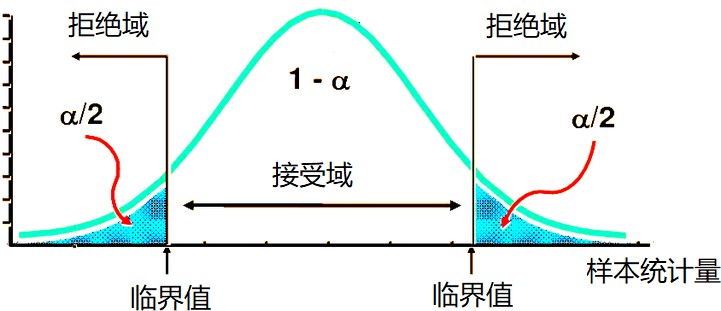双侧检验：

单侧检验：

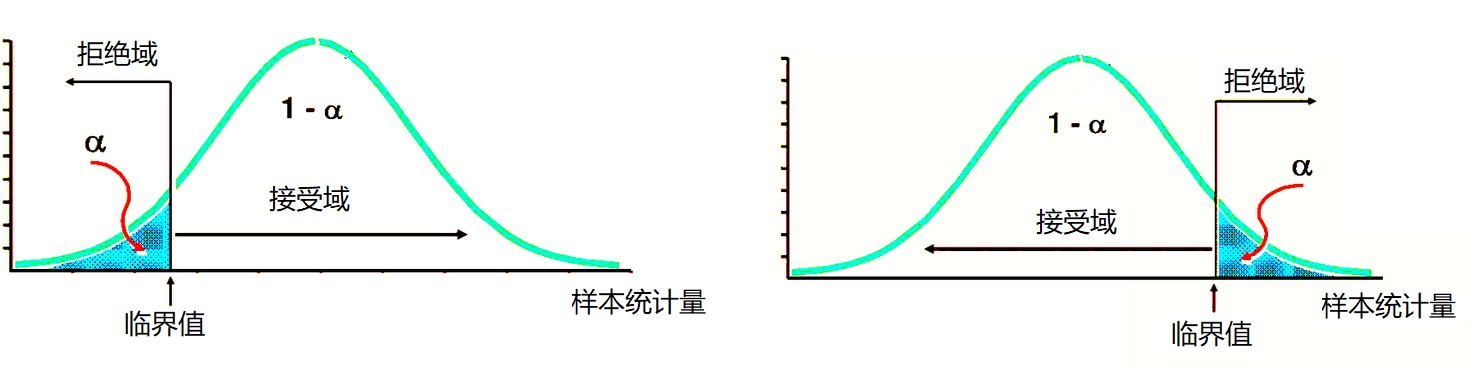
这时，我们的检验逻辑就变化为：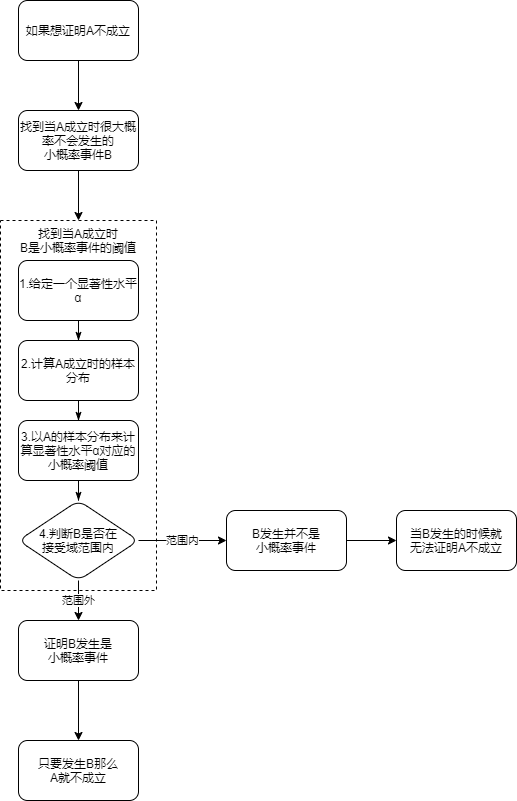

* 附录

  1. **如何判断一个样本统计量符合什么分布：**

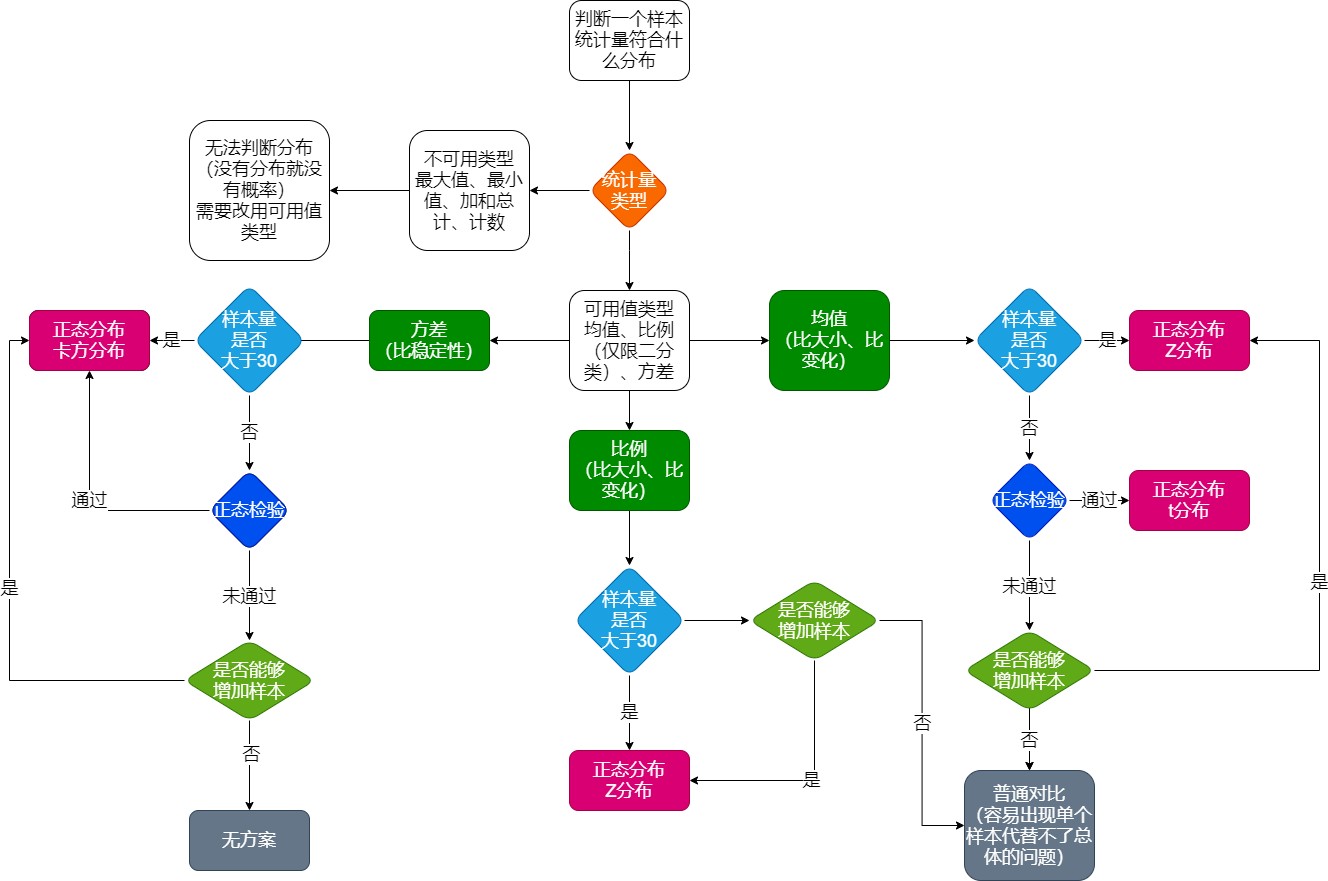
统计分布（Z分布，T分布，卡方分布）

1. T分布与标准正态分布（Z分布）都是以0为对称的分布，T分布的方差大所以分布形态更扁平些
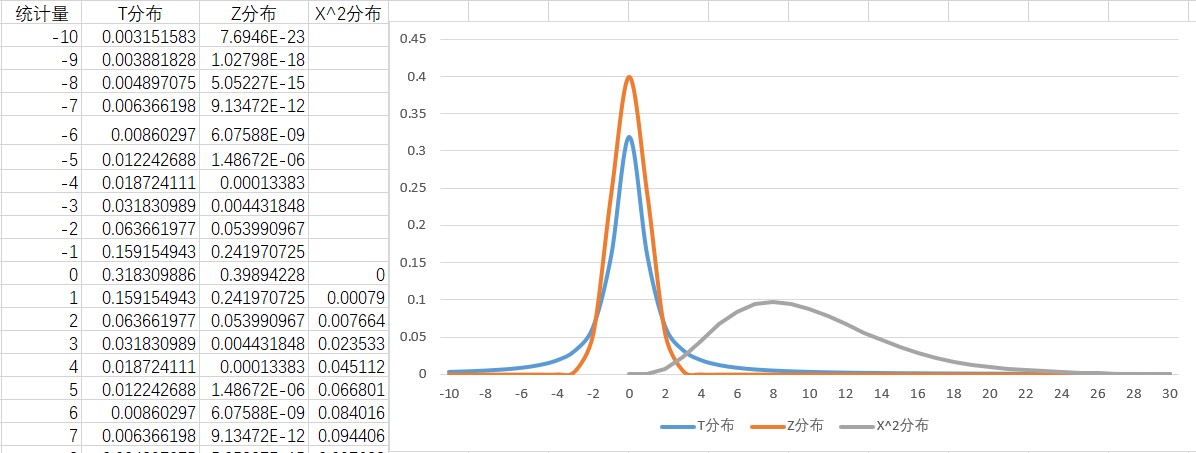2. 卡方分布是大于0的右偏分布，随着自由度的增加会趋近于正态分布（注意不是标准正态分布）

多个总体问题：

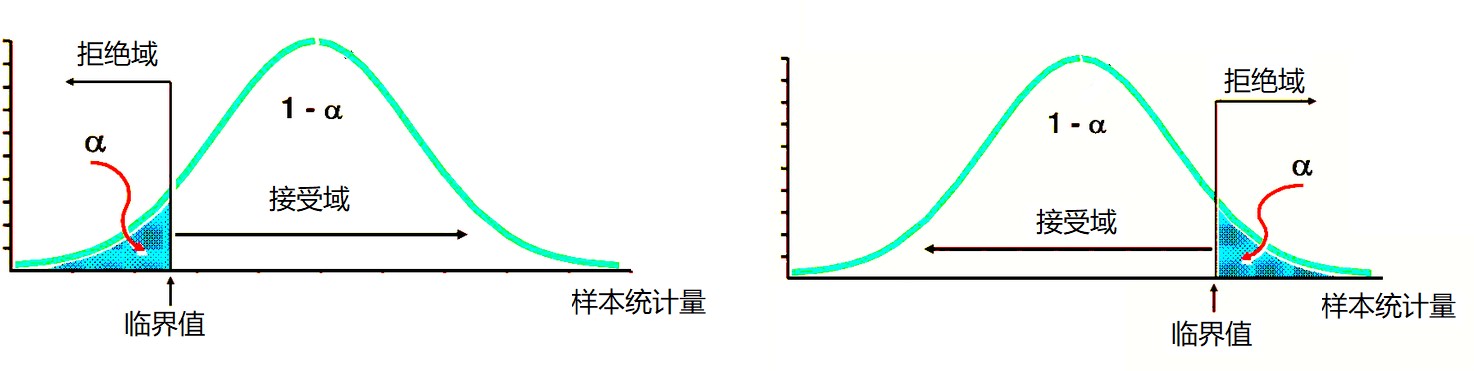
  1. **不同分布的拒绝域**

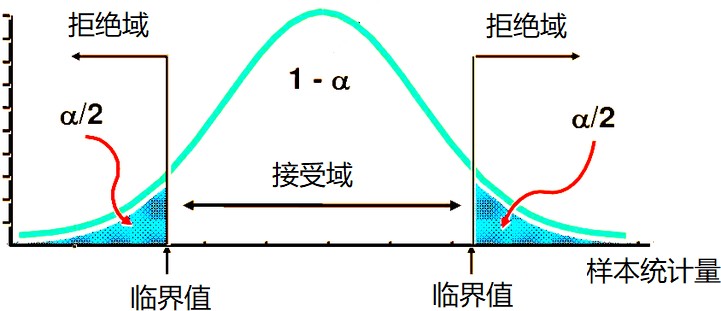
对称型（Z分布、t分布）： 双侧检验：

单侧检验：

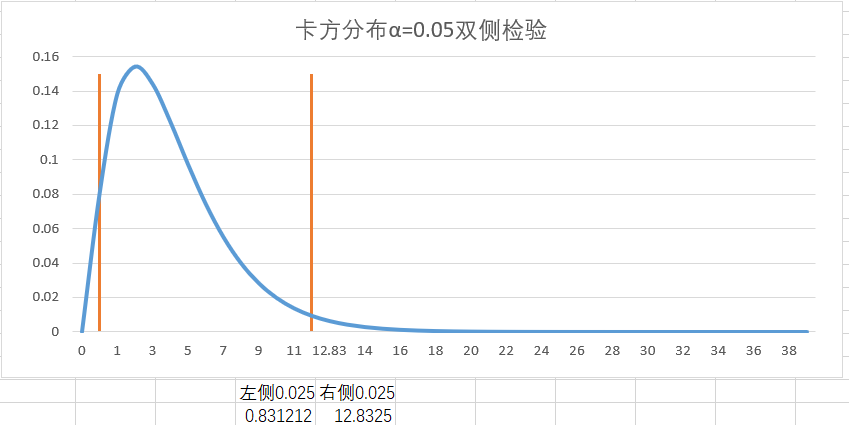
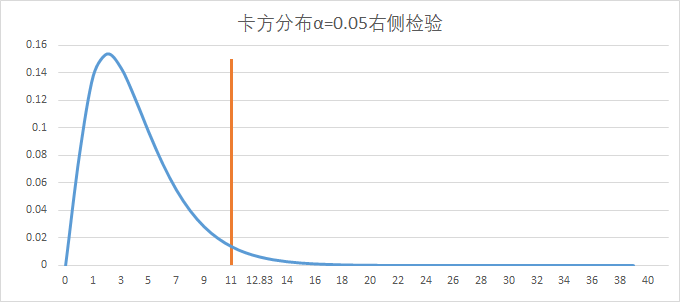
非对称型（卡方分布、F分布）： 卡方分布：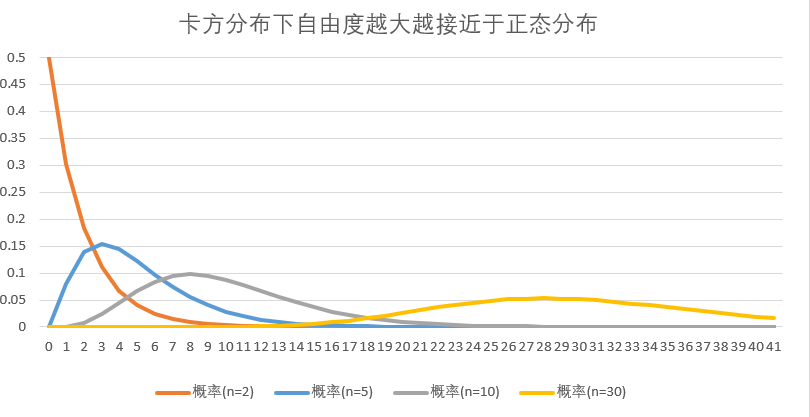

拒绝域：
（卡方分布在左侧的拒绝域特别小，所以拒绝的区间的值也比较少），所以卡方检验的拒绝域一般 放在右侧。F分布同理

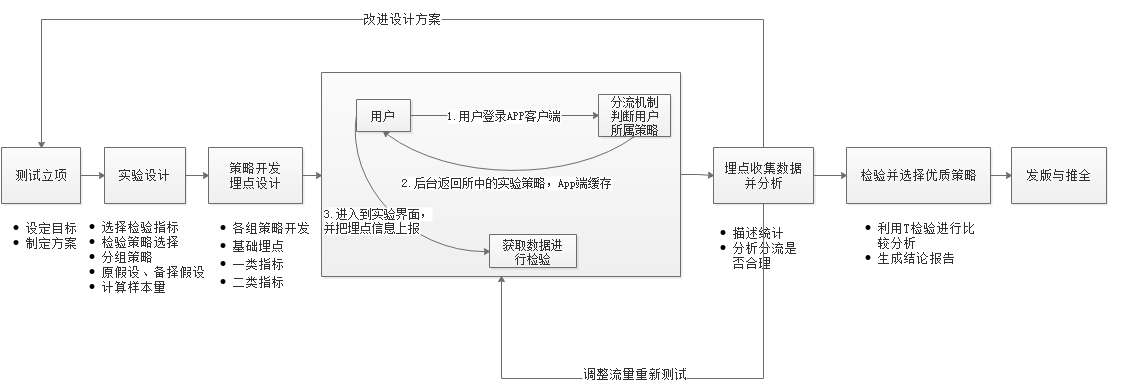
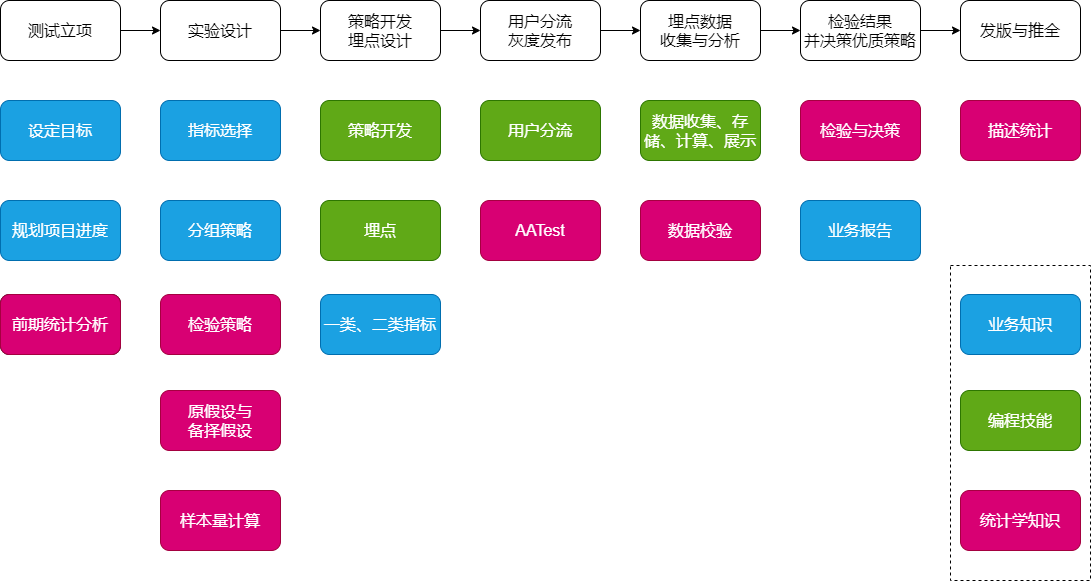
学习企业的ABTest的关键流程

整体实验设计与分析流程

企业业务问E

确定业务目-‘

选
选 酶 i+

程 假设准往早假设

计 笢 录 小 样 本 呈

选择检醮 咯

设 十分组策咯

统计检验
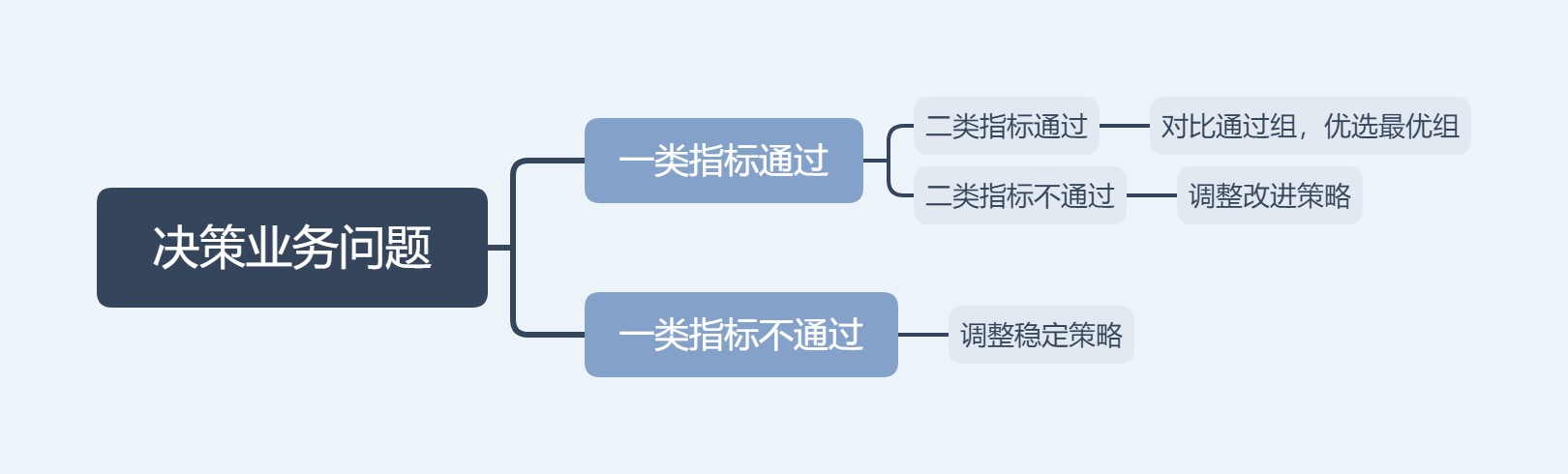
决策业务结果

实验设计

  1. **确定业务目标**

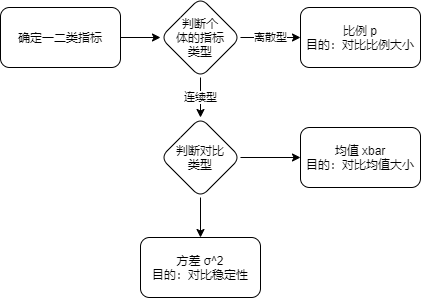
选择检验指标

1. 选择一类指标

一类指标：不能容忍变差的指标； 二类指标：目标提升的指标。
如何确定一类指标？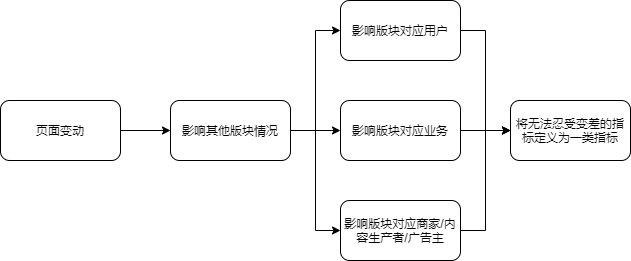

场景举例：

选择统计量

  1. **确定原假设与备择假设**

两类统计错误的防范

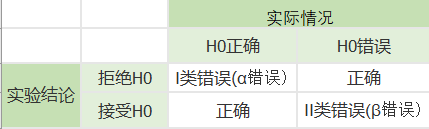
1、 α+β不一定等于1。
2、在样本容量确定的情况下，α与β不能同时增加或减少。
3、统计检验效力（1-β）当H0为假时,得出拒绝H0的正确结论的概率,被称做检验的效力

I类错误防范 ：
小概率α设置小些( 避免小概率的触发) 增加样本量（使异常数据的影响降低）

II类错误防范：
调大α（增加小概率的触发） 但是接受I类错误的代价远比II类错误的代价要大，所以不予使用II类错误概率只能在实验结束后才能计算发生二类错误的概率，这是一个事后值。所以在事前 设计我们一般不考虑这个问题。默认二类错误的概率为20%。

样本量计算

统计学上根据统计量抽样分布和边际误差确定样本量
样本量计算工具：http://powerandsamplesize.com/Calculators/Compare-2-Means/2-Sample-Equali ty
业务层面是以一类错误临界值二类错误临界值计算

其中，区间估计算式：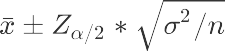

检验策略选择、设计分组策略

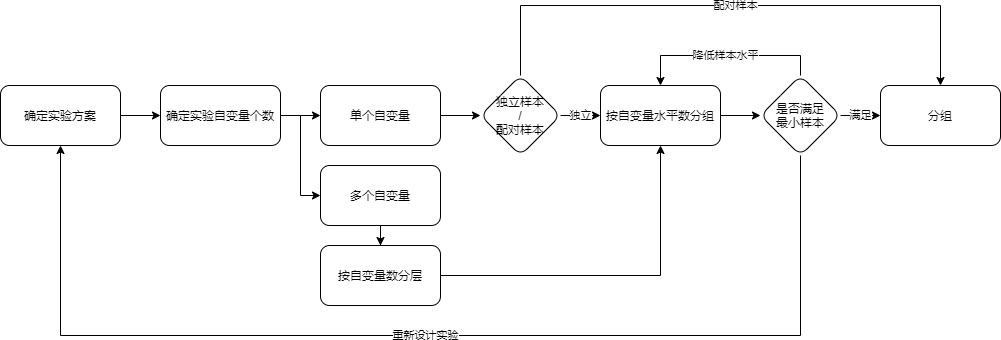
  1. **当企业没有AB测试的条件的时候，如何解决问题？**

1. 没有系统
2. 用户量不够
3. 时间成本高

实验结论分析

  1. **决策统计检验**

做实验决策可以通过统计量 及 统计量的P值来实现。
同时也可以通过样本量分布和显著性水平来确定拒绝域和接受域，从而拒绝或者接受结果。见假设检验 部分。

  1. **决策业务问题**