《Auto-Encoding Variational Bayes》
开始之前po一段知乎上抠的，作为概率论知识的唤醒：
image.png
摘要没看太懂，感觉就是构造模型对大数据构造的概率模型进行学习与推理，之后再议。

1. Method

本节的策略可用于推导具有连续潜变量的有向图形模型的下界估计量(随机目标函数)。

1.1 Problem senario

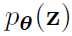i.i.d.指独立同分布。image.png就是一个独立同分布。假定数据中包括未观测的连续任意变量z。整个过程包括两个步骤：1，由先验分布image.png获得z值；2，x由条件概率image.png获得。假设这两个先验值来自分布image.png和image.png，且这些分布关于\theta和z的概率密度值是可微的，这两个值也都是未知的。
模型主要会解决棘手问题（Intractability）和大的数据集（A large dataset），并着眼于三个具体场景：1，\theta的估计；2，通过已知的观测量x和参数\theta得到潜在变量z；3，对x的有效近似边际推断。
为了解决上述问题，提出识别模型image.png，作为对真实后验分布image.png的近似。本文也会介绍介绍一种结合生成模型参数\theta学习识别模型参数\phi的方法。image.png将作为encoder，image.png作为decoder。

1.2 The variational bound

边缘相似性由每个数据点的边缘相似性之和构成，可以写作：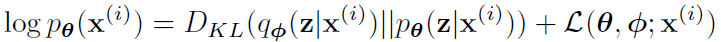
image.png
这里学习一下KL散度。KL散度也叫相对熵，等价于两个概率分布的信息熵（Shannon entropy）的差值，可以作为最大期望算法的损失函数。等号右边第一项是近似分布与真实后验分布的KL散度，第二项叫做数据点i的边缘相似度的下界，可以写作：
image.png
亦可写作：
image.png
我们想要对这个下界进行微分和优化。

1.3 The SGVB estimator and AEVB algorithm

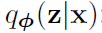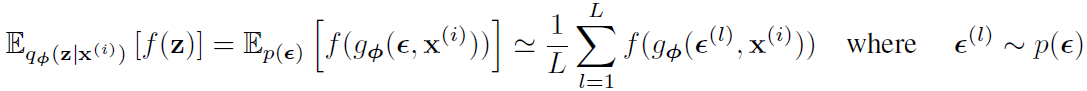
该部分介绍下界的估计函数。近似的后验估计为image.png。对于其中未观测到的z进行一个微分变换。image.png。这里进行一个知识补充，蒙特卡罗（Monte Carlo）法，即为通过大量随机样本，去了解一个系统，进而得到所要计算的值。
image.png
把这个式子代入上面那个边缘相似度下界第一个式子，即把f(z)用具体的关于z的函数替代。
image.png

代入边缘相似度下界第二个式子可以得到：
image.png
从数据集X中取N个数据点，我们可以构造一个基于小批量的完整数据集边际似然下界的估计，
image.png
\X_M是从包含N个数据点的完整数据集X中随机抽取M个数据点的样本。实验发现只要M足够大，每个数据点的样本数L可以设置为1。上面那个式子第一项(近似后验与前验的KL散度)作为正则化器，而第二项是一个预期的负重构误差。获取\theta和\phi的具体算法AEVB如下：
image.png

1.4 The reparameterization trick

有三个方法来计算\g_phi()和\sigma.

  1. 简易的逆CDF。这里介绍一下CDF和PDF。CDF全称累积分布函数 (cumulative distribution function)，是PDF的积分，是一个最终等于1的不减函数。而PDF全称概率质量函数（probability mass function)，就是描述概率变化的情况，比如正太分布就是中间高两头低。而逆CDF就是求特定分布的参数的过程。
  2. 令g()=location + scale · \sigma。
  3. 组合:通常可以将随机变量表示为不同的辅助变换。

2. Example: Variational Auto-Encoder

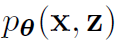这个部分利用神经网络实现概率encoderimage.png，之前有说这个encoder是生成模型image.png的后验的近似。两个参数\theta和\phi通过AEVB算法进行优化。设潜在变量的先验为中心各向同性多元高斯分布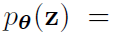image.pngimage.png。令image.png为多元高斯分布（实值数据）或伯努利分布（二分数据），通过MLP得到参数分布。因为p比q更棘手一些（why），我们可以让变分近似后验q是一个具有对角协方差结构的多元高斯。
image.png
这里的均值\miu和方差\sigma都通过MLP得到的。用1.4里面方法二，image.pngimage.png，这里的乘法符号是点乘。代入之前推出的这个式子：
image.png
得到：
image.png
image.png是伯努利或高斯MLP。

3. Experiment

实验训练了来自MNIST和Frey Face数据集的图像生成模型，并根据变分下界和估计的边际似然值比较了学习算法。可以看到和Baseline对比效果明显更好。
image.png
image.png

其实看完还有些晕乎乎的。结合别人的博客再来分析一下VAE到底在干嘛。
首先要理清楚它的目标，之前也提过：Z是隐变量，我们假设它服从某种分布，希望能通过Z生成独立同分布的目标数据X。简单来说，希望训练一个X=g(Z)的模型。
image.png
这样，有真实分布X和X_hat，KL散度无法知道它们到底是不是一个分布（KL散度只能通过概率分布表达式来计算相似度），VAE便来解决这个问题。可以回忆一下GAN其实也为了这个目的在干差不多的事情，有一个生成器和判别器，为了让生成器生成更合理的分布，就用判别器来纠正它。接下来就是干货，不搬运了，详情见链接。一个挺好的图放一下：
image.png