E(n) Equivariant Normalizing Flows

nips 2021
是等变图神经网络的后续工作。做分子生成的。先明确概念。

Normalizing Flows

定义一个可逆变换。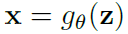，以及一个基础分布，（比如正态分布），产生一个较复杂的分布。令，。Jf是fθ的Jacobian（雅可比矩阵是函数的一阶偏导数以一定方式排列成的矩阵）。
更通俗易懂一些关于normalizing flow的详解见这里。
比较特殊的例子，连续时间normalizing flow，φ是神经网络，动态的，需要高阶可导且利普希茨连续（是一个比通常情况更强的光滑性连续条件）。

Equivariance

同一个概念，比起ICML这里的概念解释得更通俗易懂一些（无语）。这个工作同样针对在n维欧几里得group的，写作E(n)，这个group的一个重要特性就是里面的变换会保留欧几里得距离，意思就是x1和x2变换之前和变换之后的欧几里得距离是不变的。

这一段对于基本思想的理解很重要，想要获得的分布要有invariance，而对其进行的变换需要有equivariance。有等变变换g和不变分布p_Z时，且有x=g(z)，则p_X是不变的。所以当拥有p_Z和g时就可以设计一个不变分布x。此外，如果有f=g-1，那么f也是等变的。

Method: E(n) Equivariant Normalizing Flows

分布，zx是Mxn维的隐坐标，z_h是Mxnf维的隐特征向量。是一个可逆变换，可以产生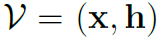，即每个节点包含节点特征向量和多维坐标。根据之前的已知最大流概念中逆变换求复杂分布的公式，有：
，
目的：设计的p_V需要对x是invariant的，对(x,h)的置换也是invariant的。总体就是需要学到p_V分布，学到它的前提就是得到它需要p_Z和f，前者invariant，后者equivariant。
因此需要对fθ有等变和可逆的限制。用下面的式子来近似fθ，将fθ定义为微分方程，并用得到了EGNN，φ。定义x和h为随时间变换的函数。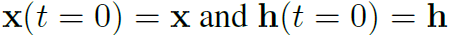，，z是隐变量。

z的分布定义为高斯分布。
还有个问题就是h可能是离散的，而标准流是针对连续分布的，解决方案很复杂就不细看了。简而言之，不是直接训练离散属性h，而是将属性提升到连续变量h。提升方法取决于一个特征是分类的还是有序的。
最后，节点的数量M可能会因数据的不同而不同。在这种情况下，我们使用M个类别的一个简单的一维类别分布pM扩展模型。这个分布pM是通过计算某个类别分子的数量并除以分子总数来构建的。
训练整体流程：


目标函数就是最大化上面图的右边四项。

听了一下这篇的oral presentation。总得来说normalizing flow就是一种生成模型，很容易联想到VAE，同样都用简单的分布（比如正态分布）来找到复杂分布，normalizing flow的要求就多一点，因为要知道那个符合简单分布的变量以及复杂分布的变量之间的函数关系，这个函数还要是可逆的，所以也相较黑盒一些的decoder而言更有道理一些。所以用normalizing flow就会要求去近似这个函数。