《Understanding contrastive representation learning through alignment and uniformity on the hypersphere》

本文确定了两个与对比损失相关的关键性质，一个是来自正对的特征的对齐，另一个是超球上（归一化的）特征的诱导分布的均匀性。文章证明了这两个性质其决定作用，并对其进行了量化与优化。
为什么要把特征放在超球（hypersphere）上，即以超球面作为特征空间，作者说有以下优点。一个是固定的向量表示为有大量点乘的机器学习提供稳定性。另一个是易于线性分类（图二）。要注意将特征映射到超球面空间的编码器，需要保留必要的信息。摘要中提到的关键性质，对齐（alignment）和均匀（uniformity）对齐有利于编码器将相似的特征分配给相似的样本。均匀性倾向于保留最大信息的特征分布，即单位超球面上的均匀分布。（图一）
image.pngimage.png
文章主要贡献：
提出了alignment和uniformity的量化指标，作为表征质量的两个衡量标准，具有理论动机。证明contrastive loss渐进地优化了alignment和unifomity。经验上，发现指标和下游任务绩效之间有很强的一致性。尽管形式简单，但我们提出的指标在没有其他损失的情况下直接优化时，经验上比对比学习在下游任务中导致相当或更好的表现。

1. Related Work

无监督对比表示学习。
单位超球面上的表示学习。在对比学习之外，许多其他的表征学习方法也将它们的特征归一化到单位超球面上。在变分自动编码器中，超球潜在空间表现得比欧氏空间更好。在单位超球面上直接匹配均匀采样点可以提供良好的表示。作者正式研究了超球几何和流行的对比表征学习之间的相互作用。
单位超球面上的分布点。一般解决关于核函数的pairwise potential（对势）最小化问题。本文提出的均匀度度量是基于高斯势的，它可以用来表示一类非常一般的核，并与普遍的最优点配置密切相关。

2. Preliminaries on Unsupervised Contrastive Representation Learning

对比学习假设了一种对正数对进行采样的方法，表示应该有相似表示的相似样本。实践中，正样本对一般是同一个样本的两个独立随机增强版，比如同一张图片的两个裁剪（crop）。
令image.png为n维的数据分布，image.png为正样本对分布。有如下假设，满足：
image.png
对比学习中的典型映射image.png，将数据映射成m维的l2归一化的特征向量。损失函数定义（虽然形式很简单但是不是很懂为什么要这样，如果从相似的表示乘积较大的方向想的话，那就是要尽量最小化这个损失，似乎挺合理的）如下：
image.png
M为固定的负样本数量。image.png为超参数。此外，作者认为对向量表示进行归一化处理是很有必要的。再引入一个概念叫infomax原则，就是将上式视为一个下界然后最大化它。但是有时并不合适。

3. Feature Distribution on the Hypersphere

对比损失鼓励学习的特征表示为正数对是相似的，而将随机抽样的负数对中的特征分开。传统观点认为，表示应该从正数对中提取出最共享的信息，并对其他噪声因素保持不变。因此，损失应优先考虑以下两个属性：
alignment：形成正对的两个样本应该映射成相近的特征，因此(大部分)不受不必要的噪声因素的影响。
uniformity：特征向量应大致均匀分布在单位超球S1上，尽可能保留数据的信息。
为了对以上内容进行验证，对于数据集CIFAR-10，数据表示通过以下三个方法获取：
image.png
所有这三种编码器共享相同的基于AlexNet的架构，将输入图像映射到S1中的二维向量。预测学习和对比学习都使用标准的数据增强来增强数据集和样本正对。论文中的图总结了验证集特性的结果分布，就不放了。图证明了非监督对比学习的特征分布最均匀，对于正成对的特征也是距离比较小的。
作者说从之前那个公式也可以看出来这一点。由p的对称性衍生如下公式（用log除法变减法一步推出来）：
image.png
由于image.png项总是正的且有下界，所以想要更小的image.png也就是更对齐（感觉前面猜测是对的）。完全对齐时有image.png。因此，最小化该loss等价于优化（这里变成1我的理解是因为f(x)和f(y)相等，所以那里随便放一个值，影响loss的在后一项）：
image.png

4.1. Quantifying Alignment and Uniformity

提出两个loss，也就是对alignment和uniformity进行量化。

4.1.1. Alignment

对齐就用距离来搞。
image.png

4.1.1. Uniformity

之前提到超球面上分布点的potential最小化问题。这里利用gaussian potential kernel，对于两个点u和v（右半边怎么等过去的，疑惑，于是我的强行解释又来了，拆平方项=u^2+v^2-2uv=1-2uv，但是感觉二范数似乎不该这么拆）：
image.png
然后loss就是取它的对数：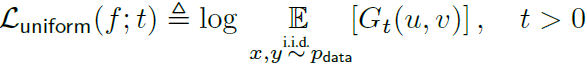
image.png
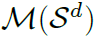t是个固定的参数。接下来给了个定义：image.png代表超球空间image.png上的标准化表面测量。image.png是borel概率测量的集合。image.png是下式的唯一解：
image.png
引入概念，测度的弱收敛（weakness convergence of measures），当\miu_n对\miu弱收敛，便有：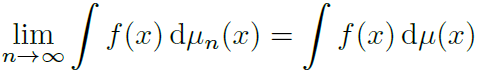
image.png
上面的那个式子对均匀分布弱收敛。感觉就是取极限就可以近似到什么就叫对什么弱收敛。
image.png
这个式子对image.png弱收敛。
下面这个图展示了KDE
image.png

4.2. Limiting Behavior of Contrastive Learning

两个定义：
image.png