E(n) equivariant GNN

ICML 2021

Equivariance

首先明确概念Equivariance。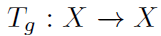是X上的变换集合，g是属于G的抽象集（abstract group，关于这个概念网上没有解释，有人说abstract可以看作any），我们说函数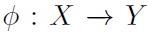对g是等变的，如果在其输出域存在等价变化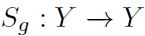，使得：。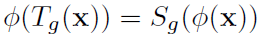
写成符号形式就很难懂。用一个实例来解释这个概念。其实只用关注上面最后一个式子。用通俗的语言说，当转换函数φ是等变的时，对x先进行T变换再进行φ变换，输出的结果与先操作y=φ(x)再对y进行T变换的结果是一样的。对于一个函数，如果你对其输入施加的变换也会同样反应在输出上，那么这个函数就对该变换具有等变性。在这篇文章的背景下，进行了三种类型的等变：translation（以tranE为代表的加法），rotation以及reflection（以rotatE为代表的乘法），以及permutation。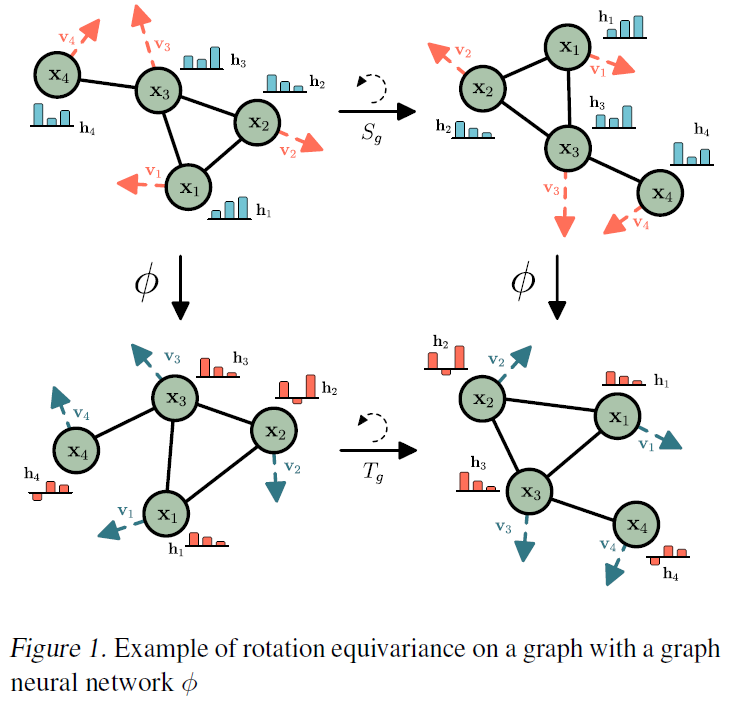

GNN

接下来介绍文章的另一个主体：GNN。GNN是置换等变的，这个很好理解，就是GNN输入是节点随机初始化embedding，如果对节点顺序做置换，输出的embedding当然也会进行同样的顺序置换。GNN普遍形式如下，其中的φ函数就是MLP。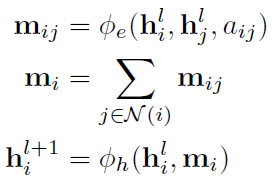

Equivariant Graph Neural Networks

接下来切入正题，等变图神经网络。对节点的表示除了embedding h之外，还多出来了坐标（coordinate）x，也是多维向量。等变图卷积层（EGCL）定义如下：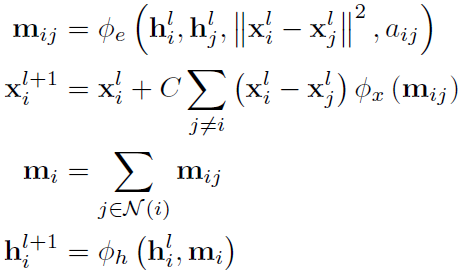

φ_x是一个MLP，将nf维的输入变成标量输出，在这里相当于把embedding m_ij变成了一个标量。C=1(M-1)，M是节点个数。

Analysis

接下来就是证明等变的理论分析部分。之前提到这个EGNN有三个等变性：translation，rotation（和reflection），和permutation。Q为nxn的正交矩阵。当EGCL是对x等变转换的时候，有：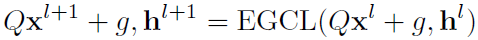

注意，EGNN里的x是等变的（equivariant），而h是不变的（invariant）。

Extending EGNNs for vector type representations

首先是对于粒子动量（particle momentum）。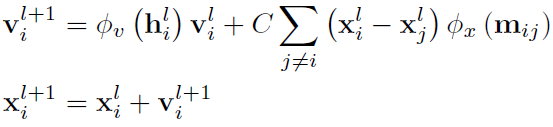

这里的v是速度，x相当于位置，φ_v同样是将embedding投影到标量的函数。

Experiments

N-body System

第一个实验，N体系统。实验目的是预测一组带电粒子的运动。具体到数据集就是该系统由5个带正电荷或负电荷的粒子组成，它们在三维空间中有一个位置和一个速度。其中包含的等变性体现在如果粒子平移或旋转，轨迹也会平移或旋转。任务就是预测在规定的timestamp之后粒子的位置，输入有位置和速度以及带电正负。对比实验结果就是EGNN的MSE最小。（比较不明白的是怎么用GNN做这个实验，个人推测就是邻居信息聚合下的消息传递）。

Inferring the edges

边的推断在之后的分子实验里会用到。因为分子数据集里只有三维坐标，没有图的邻接矩阵。因此两点是否连边需要进行推断。未知的是e_ij，使用软估计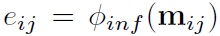，加上一个sigmoid，相当于给m加了一个attention。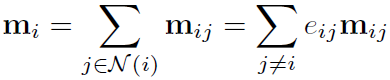

Graph Autoencoder

第二个实验，其实就是VAE，不同的是VAE是用一个向量表示图的隐变量，而这里有M个隐变量向量。x在这里是加入节点的noise，主要是解决对称图的限制。下图加了noise才能成功区分这些点。而加入了x让noise可以更简单地推广到GNN里。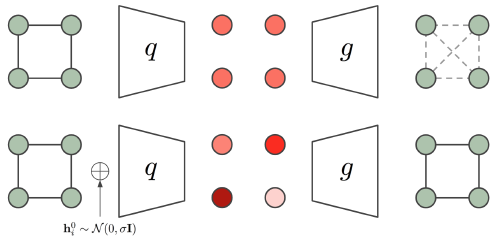

Molecular Data

首先介绍数据集QM9。QM9包含一些小型分子，每个分子至多由29个原子组成，每个原子都有其3D位置，会有one-hot向量说明是什么原子（H, C, N, O, F），标签是分子的化学性质。对于分子有个特殊情况需要注意：当发生平移和旋转时，对于性质的预测我们要的不是等变性，而是不变性。所以EGNN坐标x是不变的。所以跳过x的更新公式，模型也变成invariant的了。

补充一下关于EGNN的等变性的证明：

回忆一下想证的东西：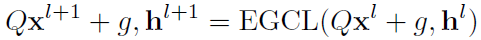


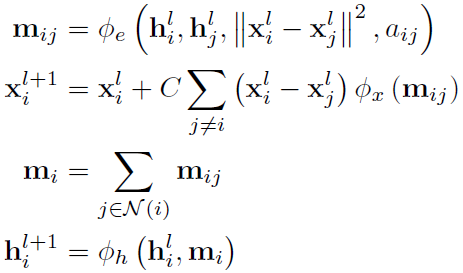
首先可以得到：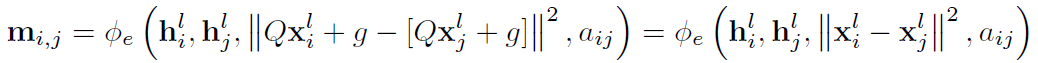

Q的消掉可能有点难想到，其实就是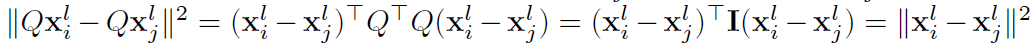
所以m_ij是invariant的。再证证x的equivariant。equivariant就是对l层x施加的translation和rotation会体现在l+1层的x上。下式可证：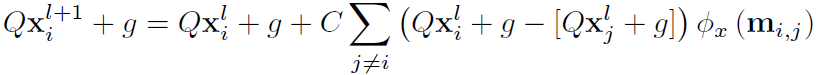

推导过程：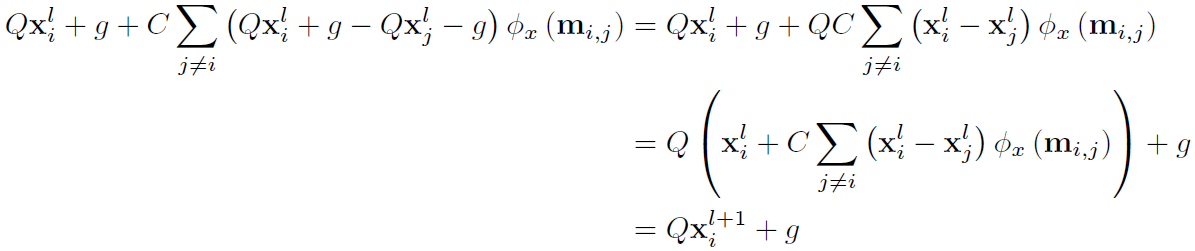

证毕。