《Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations》
通篇概念和实验偏多,这里就简谈一下收获,论文有点难懂,没咋细读,以后有机会再研究。收获主要来自油管大佬的视频。收获主要来自两个方面,什么是disentangled representations,以及这篇论文的contributions是什么。
VAE
首先看什么是disentangled representation,这里不得不首先提VAE。AE即autoencoder,其组成部分为一个encoder和一个decoder,输入一个image用x表示,encoder把它变成相应的representation,decoder又把这个representation变回x,计算和原本x的reconstruction loss来训练这个autoencoder。VAE新引入了隐变量(latent variable),一般用z表示。image进了encoder之后不急着走解码,VAE从input中获得z,这个z符合某种概率分布,在VAE中要求符合标准Gaussian分布。注意这里是好几个分布,假如有四个z,那么就让模型学到四组mean和standard deviation来表示这四个z所存在的分布。最终在四个分布中采样,组成的新的vector来重构那个x。那么VAE具体的loss是什么呢?下面这个式子就是。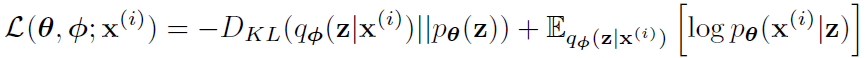
第一项是一个KL散度的计算,概率分布q就是由输入x得到的隐变量z的分布,p是先验,作者让它是标准高斯,也就是说使z的分布贴近标准高斯;第二项是一个期望,让在得到的z的分布的基础上得到x分布的可能最大化,也就是减小重构loss。
Disentangled
解耦表示,顾名思义,大体含义就是该种表示可以分离不同的factor。举个具体例子就是对于VAE,里面的x的表示为r(x),当改变一个z_i的时候,r(x)中的某个factor也会变化。再形象点,如果说x是猫的图片,那z1z2z3z4可以是颜色,大小,皮毛长度等等,相互之间毫无关联,且共同影响着猫的形象。
Contribution
搞懂了上面的东西就可以看contribution了,实验方面的贡献不加赘述,直接从唯一一个理论成果下手。作者证明了假如没有那个假设的z的分布,是不可能进行disentangled representation的学习的。作者抛出了一个理论:
尽量挨个看不懂的符号和式子解决吧。首先看p(z)那个,意思就是z_i之间相互独立,也就是满足disentangled的条件。接下来就是对z进行一个f函数变换,变换之后那个求导式子就是变换之后的z之间不相互独立了。感觉很神奇,有空看看证明。这一大段想说明什么呢?就是本来满足disentangled的z一旦被变化一下就不满足这个条件了,所以就证实了作者之前说的,z只能被提前假设,它的双射变换有infinite family,而满足解耦表示的只有它自己一种。

