nips 2013
《Stochastic blockmodel approximation of a graphon: Theory and consistent estimation》

摘要里可以看到很多船新概念。第一个ExGM，exchangeable graph model，而用来定义这个ExGM的东西就是我们要研究的graphon。而这篇文章的重点其实就如标题说的，如何通过SBA和网络（我猜是graph。）来产生graphon。
graphon存在的意义是什么呢，是一个可以保留一串图像的局部和全局信息的东西，用可度量的函数来表示，写作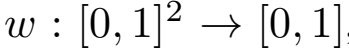image.png（熟悉得可怕），同一个graphon可能对应多个w，只要保持原来的度量。
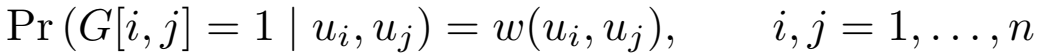
接下来说说graphon的详解。首先看看image.png已知n和w如何构建一个任意图。首先通过[0,1]的均匀分布给每个节点一个标签，这些标签就是u_i和u_j，然后通过w给节点i和j之间连边赋一个概率值。
image.png
这里的G[i, j]指图的邻接矩阵里(i, j)那个entry。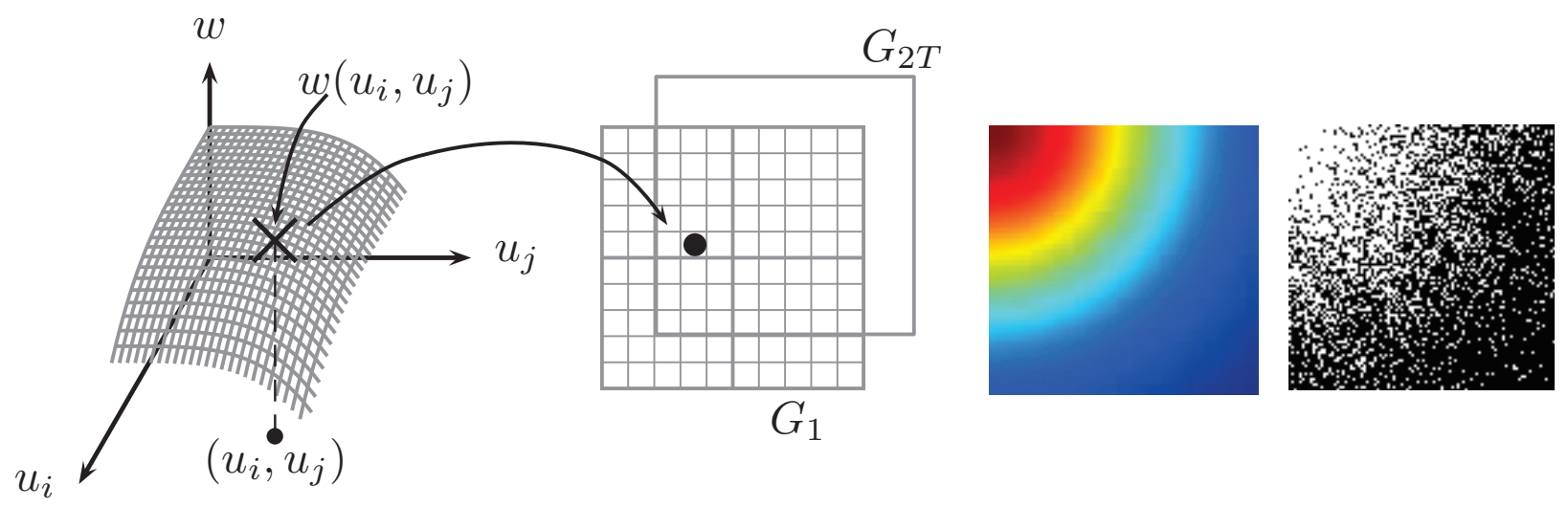
image.png
左边就是一个通过概率给G赋值的过程，值得注意的是有2T个G，因为毕竟是通过概率的。中间是graphon的热力图，右边是随便生成的一个图。
这个形式如果反过来就出现了本文要讨论的问题，如果我们有2T个G的序列（注意是有向图），可以产生w吗？
本文提出的w是分段利普西茨的的。

Stochastic blockmodel approximation: Procedure

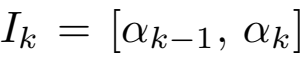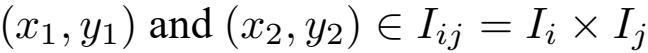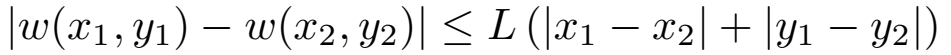
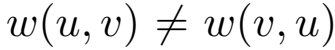首先w符合连续利普西茨，有image.png，image.png，L是个大于0的常数，有image.png：
image.png
此外，image.png，图是有向图，邻接矩阵不是对称的。
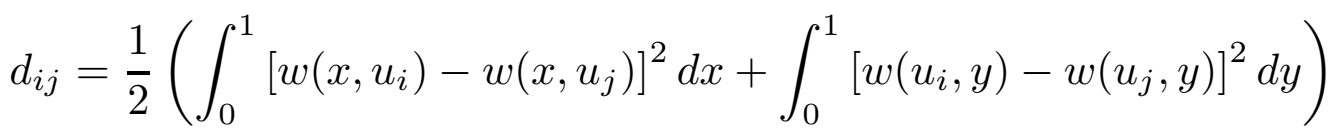
SBA设计的基本思想是如果两个节点的标签u_i和u_j接近，那么image.png和image.png也会接近，作者意思大概就是比较相近的点，其与其他节点的亲疏关系也会比较相近。所以定义如下距离：
image.png
当u_i和u_j很接近的时候d_ij就会很小。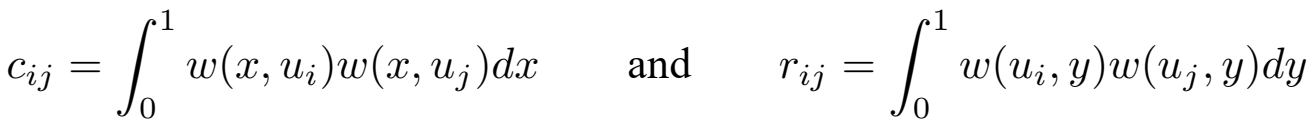
image.png
代入上面式子展开：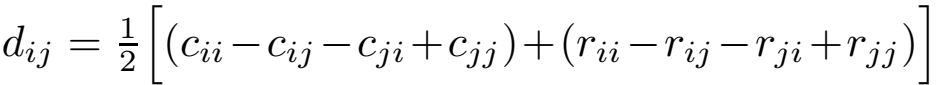
image.png
作者为c和r设计了estimator：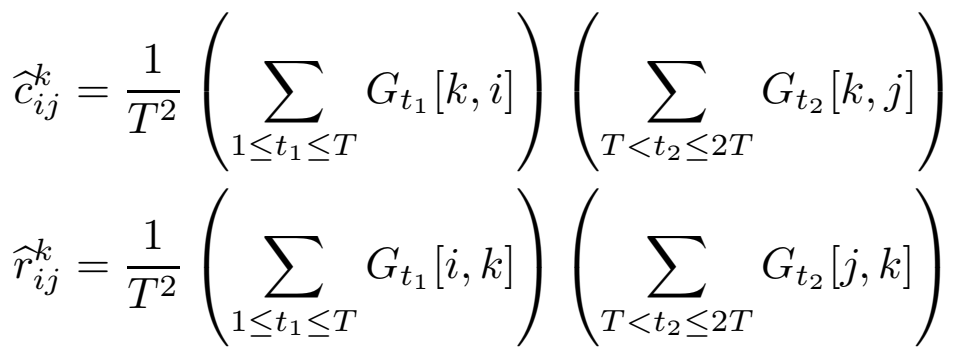
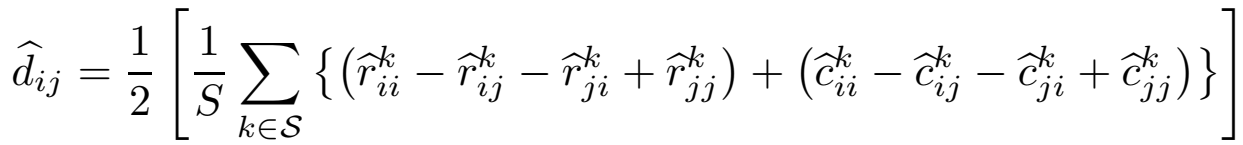
image.png
image.png
具体怎么利用上面的东西实现w的获取呢，式子如下：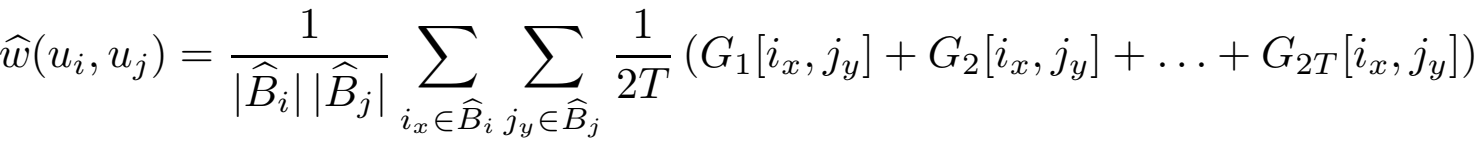
image.png
这些B是一些block，把u_i要聚类到B里面，通过观察block之间的连线来确定节点之间的连线。接下来自然产生的问题就是怎么做聚类，作者用一个算法表示：
image.png
可以跟着读一遍，其实方法很直白，就是每次迭代都选一个节点作为pivot，然后将距离小于阈值的点都归于与该pivot一个block的点，之后把这些点都排除掉，在剩下的集合中再进行一次这个迭代。

之后就是理论分析了，退退退！似乎了解这是干嘛了，等组会排到我再串起来两篇文章，然后就去搞ddi encoding和学姐说的副作用了，祝我好运！