概念

线段树的结构

线段树，也叫区间树，是一个完全二叉树，它在各个节点保存一条线段（即“子数组”），要理解线段树，必须知道如下三个问题：

  • 线段树每个节点存什么
  • 节点下标是什么
  • 如何建树

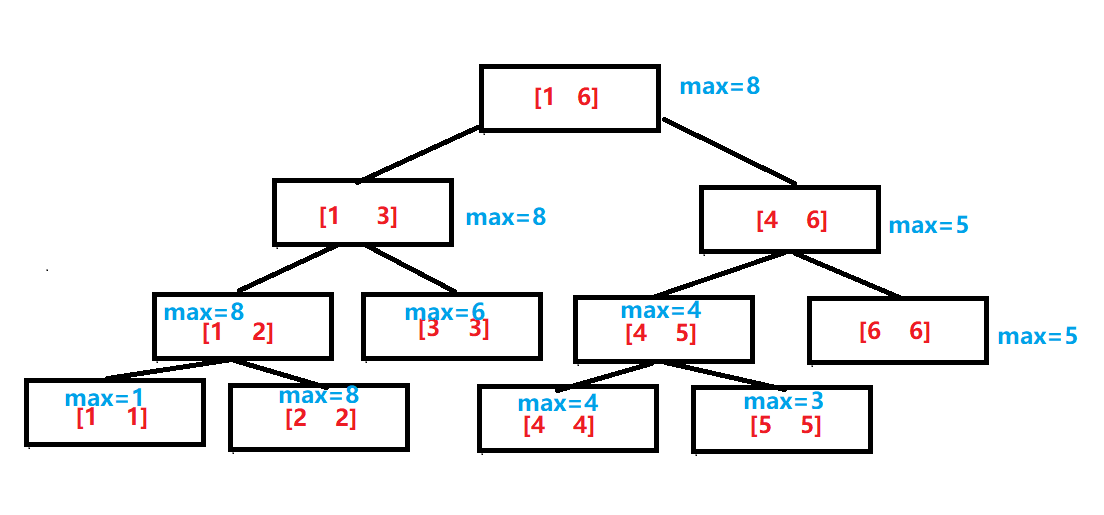
线段树 - 图1
如上图，以区间最大值来简书上述概念。
对于数组A[6]={1,8,6,4,3,5},红色代表每个结点存储的区间，蓝色代表该区间最值。

线段树每个节点存什么？

每个叶子结点的值就是数组的值，每个非叶子结点的度都为二，且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。

节点下标是什么？

对于一个区间[l,r]来说，最重要的数据当然是l和r，不过大多数情况下并不会存储这两个值，而是通过递归传参的方式进行传递。由于线段树为完全二叉树，故其父节点与孩子节点有如下关系：

  • leftChild=father>>1；
  • rightChild=father>>1|1;

    如何建树——以解决区间最大值为指向建树？

    无优化的线段树(由于完全二叉树)建树需要线段树 - 图2（2k-1 < n < 2k)空间，一般会开到4*n的空间防止RE。

  1. const int MAXNUM=100005;
  2. struct SegTreeNode{
  3.     int val;
  4. }segTree[MAXNUM];//定义线段树
  6. //线段树插入函数
  7. void pushMax(k){
  8.     segTree[k]=max(segTree[k<<1],segTree[k<<1|1]);
  9. }
  10. /*
  11. root:当前线段树的根节点下标
  12. arr:用来构造线段树的数组
  13. istart,iend：数组的起始与结束位置
  14. */
  15. void recurbuild(int root,int arr[],int l,int r){
  17.     if(l==r){
  18.         segTree[root].val=arr[l];
  19.     }
  20.     else{
  21.         int mid=l+(r-l)>>1;
  22.         recurbuild(root<<1,arr,l,mid);
  23.         recurbuild(root<<1|1,arr,mid+1,r);
  24.         pushMax(k);
  25.     }
  26. }

应用场景

线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。更可以扩充到二维线段树（矩阵树）和三维线段树（空间树）。对于一维线段树来说，每次更新以及查询的时间复杂度为O(logN)。

与其他RMQ（Range Minimum/Maximum Query）算法的区别

常用的解决RMQ问题有ST算法，二者预处理时间都是O(NlogN)，而且ST算法的单次查询操作是O(1)，看起来比线段树好多了，但二者的区别在于线段树支持在线更新值，而ST算法不支持在线操作。

简单线段树——无pushdown,单点修改，区间查询

针对上一节的线段树，我们做如下修改。

单点修改

a[3]+7后，节点更新(紫色代表更新后的max)如下，所有包括a[3]的的线段树都需要更新。 更新了a[3]后，总共有log(k)个节点需要更新

线段树 - 图3

  1. /*
  2. 更新线段树中某个叶子节点的值
  3. root:根节点下标
  4. index:待更新节点在数组中的下标
  5. addVal:更新值
  6. */
  7. void updateSingle(int root,int l,int r,int index,int addVal){
  8.     if(l==r){
  9.         if(index==l) //找到对应的值
  10.             segTree[root].val+=addVal;
  11.         return;
  12.     }
  13.     int mid=l+((r-l)>>1);
  14.     if(index<=mid) //在左子树中
  15.         updateSingle(root>>1,l,mid,index,addVal);
  16.        updateSingle(root>>1|1,mid+1,r,index,addVal);
  17.     //根据左右子树的值回溯更新当前节点的值
  18.     pushMax(root);    
  19. }

区间查询

如何寻找某个区间的最大值呢？思想是选出一些区间，使它们相连后签好涵盖整个查询区间，因此线段树适合解决“相邻的区间的信息可以被合并成两个区间的并区间的信息”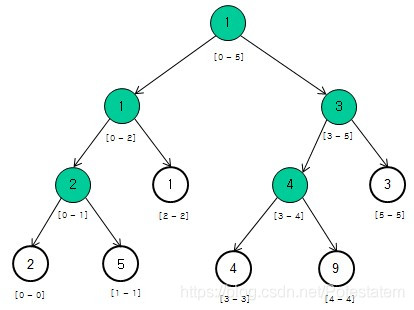
线段树 - 图4

  1. /*
  2. 功能：线段树的区间查询
  3. root：当前线段树的根节点下标
  4. [l, r]: 当前节点root所表示的区间
  5. [qstart, qend]: 此次查询的区间
  6. */
  7. int query(int root,int l,int r,int qstart,int qend){
  8.     //查询区间和当前区间无交集
  9.     if(qstart>r || qend<l) 
  10.         return INT_MIN;
  11.     //查询区间包含全部当前区间
  12.     if(qstart<=l && qend>=r)
  13.         return segTree[root].val;
  14.     //分别从左右子树继续查询,返回两者较小者
  15.     int mid=l+((r-l)>>1);
  16.     return max(query(root>>1,l,mid,qstart,qend),
  17.                 query(root>>1|1,mid+1,r,qstart,qend));
  19. }

复杂线段树——pushdown区间修改与查询

线段树的区间更新——延迟标记

区间更新指的是更新某个区间内叶子节点的值，也因为涉及到的叶子节点众多，而叶子节点会影响其相应父节点，那么回溯更新的复杂度会更高，如果一次更新完，时间复杂度不止O(logn),故引入了线段树延迟标记的概念。
延迟标记：
每个节点新增加一个标记，记录这个节点是否进行了某种修改(这种修改操作会影响其子节点)。
对于任意区间的修改：

  1. 我们先按照区间查询的方式将其划分成线段树中的节点，然后修改这些节点的信息，并给这些节点标记上代表这种修改操作的标记。
  2. 在修改和查询的时候，如果我们到了一个节点p，并且决定考虑其子节点，那么我们就要看节点p是否被标记，如果有，就要按照标记修改其子节点的信息，并且给子节点都标上相同的标记，同时消掉节点p的标记。

实例说明：
对区间[0,2]的叶子节点增加2.

  1. 利用区间查询从根节点开始找到了非叶子节点[0,2]，并将其延迟标记设置为2,更新完毕.
  2. 当查询[0,1]时，查到区间[0,2]时，发现其延迟标记非0，并且还要向下查找，把节点[0,1]的值设置为2+2=4,标记设置为2,节点[2,2]的值设置1+2=3，标记设置为2。（由于叶子节点不能向下传递，其实叶子节点的标记不起作用）并将区间[0,2]的标记设置为0;
  3. 返回查询结果[0-1]节点的值4;
  4. 当我们再次区间更新[0,1]时，将其增加3，查询到该节点[0,1]时，发现其延迟标记为2，故更新其延迟标记为2+3=5，并更新其值为4+3=7; ```cpp //线段树节点结构 const int MAXNUM=100005； struct segTreeNode{ int val; int addMark; }segTree[MAXNUM];

void pushFunc(int root){ segTree[root].val=max(segTree[root>>1].val,segTree[root>>1|1].val); }

/ 功能：根据arr[]建立线段树 root：当前线段树的根节点下标 arr: 用来构造线段树的数组 l：数组的起始位置 r：数组的结束位置 / void buildTree(int root,int arr[],int l,int r){ segTree[root].addMark= 0; //设置延迟标记 if(l==r){ segTree[root].val=arr[l]; } int mid=l+((r-l)>>1); buildTree(root>>1,arr,l,mid); buildTree(root>>1|1,arr,mid+1,r); pushFunc(root); }

/ 功能：当前节点的标志域向孩子节点传递 root: 当前线段树的根节点下标 / void passMark(int root){ if(segTree[root].addMark!=0){ //设置左右孩子的延迟标记 //注意节点可能被多次标记，故用+= int addMark=segTree[root].addMark; segTree[root>>1].addMark+=addMark; segTree[root>>1|1].addMark+=addMark; //由于是求区间最大值，故区间内加上某个值时，整体最大值也需要增加 segTree[root>>1].val+=addMark; segTree[root>>1|1].val+=addMark;

  1.     //传递后，当前标记域清空
  2.     segTree[root].addMark=0;
  3. }

}

/* 功能：线段树的区间查询 root：当前线段树的根节点下标

*/ int query(int root, int l, int r, int qstart, int qend){ //是否有交集 if(qstart>r || qend=r) return segTree[root].val; passMark(root); //传递延迟标记 int mid=l+((r-l)>>1); return max(query(root>>1,l,mid,qstart,qend) ,query(root>>|1,mid+1,r,qstart,qend)) }

/* 功能：更新线段树中某个区间内叶子节点的值 root：当前线段树的根节点下标

addVal: 更新的值（原来的值加上addVal） */ void update(int root, int l, int r, int ustart, int uend, int addVal){ //更新区间与当前区间无交集 if(ustart>r || uend=r){ segTree[root].addMark+=addVal; segTree[root].Val+=addVal; return; } passMark(root); //传递延迟标记 int mid=l+((r-l)>>1); update(root>>1,l,mid,ustart,uend,addVal); update(root>>1|1,mid+1,r,ustart,uend,addVal); //回溯更新当前节点的值 pushFunc(root); } ```

区间乘除修改与查询

应用

http://dongxicheng.org/structure/segment-tree/
https://www.cnblogs.com/jason2003/p/9676729.htmllink