并查集基础版本
优化方案
- 路径压缩（查询过程中进行）
- 按秩（不同合集的深度）合并
C++11模板
例题详解
- 亲戚关系(基础)
- 奶酪（提高）
最小体力消耗路径">最小体力消耗路径
- 思路：
- 面试题 17.07. 婴儿名字">面试题 17.07. 婴儿名字

由如下几部分构成：
集合 : parent , size(代表深度或融合大小，大的融合小的) 变量：n(并查集节点总数) ， setCount(当前连通变量总数) 方法：

构造函数初始化（iota）
find
merge

并查集算法步骤：

确定并查集数据是什么？

例子：比如说从A点到达B点，说明应存取position。当connected(A,B)时，说明存在路径到达AB

确定按什么顺序合并?

最短路径（最大值-最小值）例子

将所有路径按从小到大的顺序排列
根据路径权值顺序，将位置加入并查集，知道满足connect(A,B)条件

下雨游泳例子

将当前高度按从小到大顺序排列
根据高度从小到大遍历，将位置加入并查集，直到connect(A,B)满足

并查集基础版本

初始化

假如有编号为1, 2, 3, …, n的n个元素，我们用一个数组fa[]来存储每个元素的父节点（因为每个元素有且只有一个父节点，所以这是可行的）。一开始，我们先将它们的父节点设为自己。

int fa[MAXN];
inline void init(int n)
{
    for (int i = 1; i <= n; ++i)
        fa[i] = i;
}

查询（根节点/代表元素）

根节点的标志就是父节点是本身

int find(int x){
    if(fa[x]==x){
        return x;
    }else{
        return find(fa[x]);
    }
}

合并

先找到两个集合的代表元素（根节点），然后将前者的父节点设为后者即可

inline void merge(int i,int j){
    fa[find(i)]=find(j);
}

优化方案

路径压缩（查询过程中进行）

在查询的过程中，把沿途的每个节点的父节点都设为根节点即可。下一次再查询时，我们就可以省很多事。

int find(x){
    if(fa[x]==x){
        return x;
    }else{
        fa[x]=find(fa[x]);   //将父节点设置为根节点
        return fa[x];
    }
    /* 一行 */
    return fa[x]==x ? x : (fa[x]=find(fa[x]));    
}

按秩（不同合集的深度）合并

秩小的往秩大的合并

int fa[MAXN];
int rank[MAXN];
inline void init(int n){
    for(int i=1;i<=n;i++){
        fa[i]=i;
        rank[i]=1;
    }
}
inline void merge(i,j){
    int x=find(i),y=find(j);
    if(rank[x]<=rank[y]){
        fa[x]=y;
    }else{
        fa[y]=x;
    }
    if(rank(x)==rank(y) && x!=y){
        rank[y]++;                       /*深度相同且根节点不同，合并的树深度加一*/
    }
}

C++11模板

class UnionFind {
public:
    vector<int> parent;
    vector<int> size;
    int n;
    /* 当前【连通分量】数 */
    int setCount;
public:
    UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
        iota(parent.begin(), parent.end(), 0);/*itoa 自增+1*/
    }
    int findset(int x) {
        return parent[x] == x ? x : (parent[x] = findset(parent[x]));
    }
    bool unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            swap(x, y);
        }
        parent[y] = x;                /*将小秩合并到大秩序*/
        size[x] += size[y];
        --setCount;                    /*合并后【连通分量数】-1*/
        return true;
    }
    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
};
/* 合理范围内也需要对基础款进行魔改 ————  婴儿名字 */
class UnionFind{
public:
    unordered_map<string,string> parent_;
    unordered_map<string,int> size_;
    int n_;    /* 当前连通变量数 */
public:
    UnionFind(int _n):
        n_(_n){
        }
    string find(string x){
        if(parent_.find(x)==parent_.end()){
            ++n_;
            parent_[x]=x;
            return x;
        }
        return x==parent_[x] ? x : (parent_[x]=find(parent_[x]));
    }
    void merge(string i,string j){
        string x=find(i),y=find(j);
        if(x==y){
            return;
        }
        if(x<y){
            swap(x,y);
        }
        /*字典序最小的为根元素*/
        parent_[x]=y;
        size_[y]+=size_[x];
        /* 被合并的规模至0，便于输出答案 */
        size_[x]=0;
        n_--;
    }
    bool connected(string i,string j){
        return find(i)==find(j);
    }
    int getSize(string x){
        return size_[x];
    }
};

例题详解

亲戚关系(基础)

题目背景 若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。 题目描述 规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。 输入格式 第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。 输出格式

P行，每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。

const int MAXN=5005;
int fa[MAXN];
int rank[MAXN];
inline void init(){
    for(int i=0;i<n;i++){
        fa[i]=i;
        rank[i]=1;
    }
}
int find(x){
    return fa[x]==x ? x : (fa[x]=find(fa[x]));
}
int merge(i,j){
    int x=find(i),y=find(j);
    if(rank[x]<=rank[y]){
        fa(x)=y;
    }else{
        fa(y)=x;
    }
    if(rank[x]==rank[y] && x!=y){
        rank[y]++;
    }
}
int main(){
    int n,m,p;
    cin>>n>>m>>p;
    init(n);
    for(int i=0,x,y;i<m;i++){
        cin>>x>>y;
        merge(x,y);
    }
    for(int i=0,x,y;i<p;i++){
        cin>>x>>y;
        printf("%s\n",find(x)==find(y)? "YES" : "NO");
    }
    return 0;
}

奶酪（提高）

题目描述

现有一块大奶酪，它的高度为，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为，奶酪的上表面为。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去?

空间内两点、的距离公式如下：

输入格式

每个输入文件包含多组数据。

的第一行，包含一个正整数，代表该输入文件中所含的数据组数。

接下来是组数据，每组数据的格式如下：第一行包含三个正整数和，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的行，每行包含三个整数，两个数之间以一个空格分开，表示空洞球心坐标为。

输出格式

行，分别对应组数据的答案，如果在第组数据中，Jerry 能从下表面跑到上表面，则输出Yes，如果不能，则输出No（均不包含引号）。

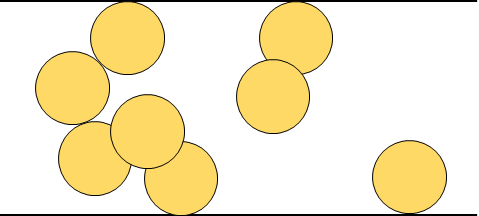
并查集 - 图17
可以将所有空洞划分若干个集合，一旦两个空洞相切或者相交，则将其放入同一个集合中。
还可以划分两个特殊集合，分别为顶部和底部，显然其执行逻辑和空洞相同。若相切或者相交，则放入同一集合。
题目可转化为判断顶部和底部是否在同一集合中。
顶部和底部相较，则说明有一个通路存在。

const int MAXN=1005;
int fa[MAXN],rank[MAXN];
using POS=int[3];
vector<POS> _pos;
/*
init find merge
*/
bool isConnected(int[] _p1,int[] _p2,int r){
    return (pow(_p1[0]-_p2[0],2)+pow(_p1[1]-_p2[1],2)+pow(_p1[2]-_p2[2],2))<=pow(2*r,2);
}
int main(){
    int T;
    cin>>T;
    for(int i=0;i<T;i++){
        int n,h,r;
        cin>>n>>h>>r;
        init(n);
        fa[1001]=1001;
        fa[1002]=1002;
        for(int i=0;i<n;i++){
            cin>>_pos[i][0]>>_pos[i][1]>>_pos[i][2];
            if(_pos[i][2]<=r)
                merge(i,1001);
            if(h-_pos[i][2]<=r);
                merge(i,1002);
        }
        for(int i=0;i<n;i++)
            for(int j=i+1;j<n;j++){
                if(isConnected(_pos[i],_pos[j])){
                    merge(i,j);
                }
            }
        printf("%s\n",find(1001)==find(1002) ? "yes":"no");
    }
}

最小体力消耗路径

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的体力值是路径上相邻格子之间高度差绝对值的最大值决定的。

请你返回从左上角走到右下角的最小体力消耗值。

思路：
将mn个节点放入并查集中，并实时维护其连通性。当某个集合中同时存在0 和m*n-1（其代表节点相同）时，便说明此路径是合法路径。
由于目标是寻找体力最小的一条路径,故将所有路径从小到大进行排列，当合并的新路径权值为v时，且满足上述条件时，则说明v为该路径的最小体力值，返回该值即可。

面试题 17.07. 婴儿名字
每年，政府都会公布一万个最常见的婴儿名字和它们出现的频率，也就是同名婴儿的数量。有些名字有多种拼法，例如，John 和 Jon 本质上是相同的名字，但被当成了两个名字公布出来。给定两个列表，一个是名字及对应的频率，另一个是本质相同的名字对。设计一个算法打印出每个真实名字的实际频率。注意，如果 John 和 Jon 是相同的，并且 Jon 和 Johnny 相同，则 John 与 Johnny 也相同，即它们有传递和对称性。

在结果列表中，选择字典序最小的名字作为真实名字。

class UnionFind{
public:
    unordered_map<string,string> parent_;
    unordered_map<string,int> size_;
    int n_;
public:
    UnionFind(int _n):
        n_(_n){
        }
    string find(string x){
        if(parent_.find(x)==parent_.end()){
            ++n_;
            parent_[x]=x;
            return x;
        }
        return x==parent_[x] ? x : (parent_[x]=find(parent_[x]));
    }
    void merge(string i,string j){
        string x=find(i),y=find(j);
        if(x==y){
            return;
        }
        if(x<y){
            swap(x,y);
        }
        /*字典序最小的为根元素*/
        parent_[x]=y;
        size_[y]+=size_[x];
        size_[x]=0;
        n_--;
    }
    bool connected(string i,string j){
        return find(i)==find(j);
    }
    int getSize(string x){
        return size_[x];
    }
};
class Solution {
public:
    vector<string> trulyMostPopular(vector<string>& names, vector<string>& synonyms) {
        int N=names.size();
        UnionFind unionFind_(N);
        for(const auto &str:names){
            int i=str.find('(');
            int j=str.find(')');
            string name=str.substr(0,i);
            unionFind_.parent_[name]=name;
            int cnt=atoi(str.substr(i+1,j-i-1).c_str());
            unionFind_.size_[name]=cnt;
        }
        for(const auto &str:synonyms){
            int i=str.find(',');
            string left=str.substr(1,i-1);
            string right=str.substr(i+1,str.size()-i-2);
            unionFind_.merge(left,right);
        }
        vector<string> ans;
        int i=0;
        for(const auto& v:unionFind_.size_){
            if(v.second!=0 && i!=unionFind_.n_){
                string tmp=v.first+'('+to_string(v.second)+')';
                ans.emplace_back(tmp);
                i++;
            }
        }
        return ans;
    }
};